Дифференциальные уравнения широко используются как аппарат математического моделирования различных объектов и явлений окружающего мира. Одним из таких их приложений является военная задача, связанная с методом наведения одного объекта на другой. При наведении ракеты на цель необходимо ее попадания в эту цель или перехват цели с минимальным промахом. Поскольку ракета управляемая и ее траекторию полета можно менять, то существует бесконечное множество траекторий. Однако, необходимо выбрать наиболее надежную согласно поставленной задаче и условиям стрельбы. Существует несколько методов наведения ракеты на цель. Одним из них является метод наведения по кривой погони. Следует отметить, что данный метод также используется при управлении торпедами и самонаводящимися бомбами. [1]
Суть метода состоит в том, что в каждый момент времени вектор скорости ракеты направлен точно на мишень. Математическая модель метода наведения по кривой погони описывается обыкновенными дифференциальными уравнениями первого и второго порядка. Будем рассматривать случай преследования удаляющейся цели.
В данной работе ставится целью использовать аппарат дифференциальных уравнений для получения и анализа пространственных и временных характеристик движения ракеты.
Считаем, что каждый объект движется с постоянной по модулю скоростью. Цель движется параллельно оси x, так что ее положение в момент времени t будет (vt;h). Ракета начинает движение в точке (0;0) со скоростью u. В произвольный момент времени ее положение показано на рисунке 1.
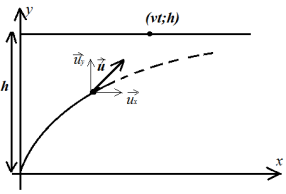
Рис. 1. Траектории цели и преследователя
Условие движения преследователя строго на цель имеет вид:![]()
При решении задачи выберем y как независимую переменную. Тогда
![]() . (1)
. (1)
Так как скорость ракеты постоянна по модулю, то 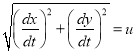 , можно записать в виде:
, можно записать в виде:
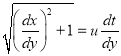 .(2)
.(2)
Продифференцируем (1) по y, тогда с учетом (2) имеем:
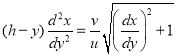 . (3)
. (3)
Обозначив ![]() получим дифференциальное уравнение
получим дифференциальное уравнение ![]() и его решение
и его решение ![]() . Неизвестную константу можно найти из начальных условий, окончательно
. Неизвестную константу можно найти из начальных условий, окончательно 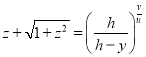 .
.
Для удобства представления данных введем параметр, характеризующий отношение скоростей преследователя и мишени ![]() , тогда, возвращаясь к производным, получим
, тогда, возвращаясь к производным, получим
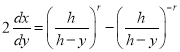 .(4)
.(4)
С учетом начальных условий (x=0 при y=0) решение имеет вид
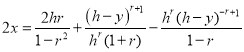 .(5)
.(5)
Получено уравнение, определяющее траекторию движения ракеты. Параметрами являются начальное расстояние между объектами и соотношение их скоростей.
Проанализируем выражение (5). Если ![]() , то
, то ![]() , с другой стороны, в этом случае
, с другой стороны, в этом случае ![]() , тогда
, тогда ![]() . Таким образом, ракета настигает цель, если
. Таким образом, ракета настигает цель, если ![]() , то есть
, то есть ![]() , и исходя из вида выражения произойдет это, если r<1, то есть скорость преследователя должна быть больше скорости мишени. При этом время между запуском ракеты и ударом определяется как
, и исходя из вида выражения произойдет это, если r<1, то есть скорость преследователя должна быть больше скорости мишени. При этом время между запуском ракеты и ударом определяется как![]() .
.
Разделив обе части равенства (4) на 2h и обозначив ![]() можно получить уравнение траектории в виде зависимости
можно получить уравнение траектории в виде зависимости ![]() от
от ![]() , то есть в нормированных единицах на расстояние до мишени в начальный момент времени.
, то есть в нормированных единицах на расстояние до мишени в начальный момент времени.
Отдельно стоит рассмотреть случай r=1. Перепишем (4)
![]()
![]()
![]() .
.
На рисунке 2 представлены виды траекторий при различных значений параметра r.
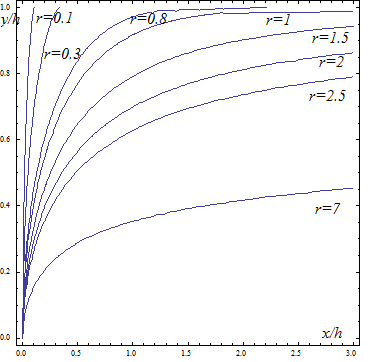
Рис. 2. Траектория движения ракеты
Помимо траектории движения интерес представляет временная зависимость. Получим выражение для времени достижения ракетой заданной координаты y. Дифференцируя по y (4) и учитывая (2) и (3) приходим к уравнению
![]() .(6)
.(6)
Решение (6) с учетом начальных условий будет иметь вид:
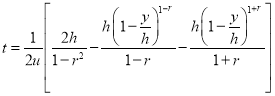 .
.
Или, если нормировать на время до удара (![]() ):
):
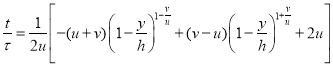 .
.
Для полного описания движения ракеты необходимо знать, как меняются составляющие ее вектора скорости. Получить выражения для составляющих скорости можно воспользовавшись (6):
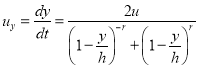 ,
, ![]() .
.
Тогда направление движение ракеты в точке, соответствующий координате y будет определяться как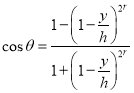 , где
, где ![]() — угол, который составляет вектор скорости с положительным направлением оси x.
— угол, который составляет вектор скорости с положительным направлением оси x.
Как уже было замечено, преследователь достигает цель в том случае, если его скорость будет больше. Найдем минимальное расстояние, на которое может приблизиться ракета, в том случае, когда ее скорость![]() . Для расстояния между объектами в произвольный момент времени можно записать соотношение:
. Для расстояния между объектами в произвольный момент времени можно записать соотношение:
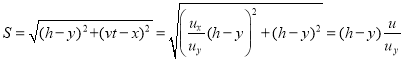 .
.
Или, подставляя выражение для составляющей скорости:
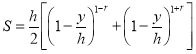 .
.
Приравнивая производную к нулю, находим, что минимальное расстояние между ракетой и целью достигается при 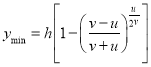 и определяется выражением:
и определяется выражением:
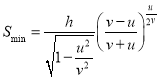 .(7)
.(7)
Представим ![]() как функцию r, то есть исследуем значение выражения в зависимости от соотношения скоростей ракеты и цели.
как функцию r, то есть исследуем значение выражения в зависимости от соотношения скоростей ракеты и цели.
-
Если r>1, то есть
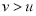 , то имеем (7). Числовое значение расстояния зависит от соотношения скоростей.
, то имеем (7). Числовое значение расстояния зависит от соотношения скоростей.
-
Если
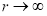 , то есть
, то есть 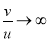 , то
, то 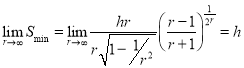 . В данном случае минимальное приближение к цели будет в начальный момент времени.
. В данном случае минимальное приближение к цели будет в начальный момент времени.
-
Если
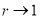 , то есть
, то есть 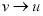 (одинаковые скорости мишени и преследователя), то
(одинаковые скорости мишени и преследователя), то 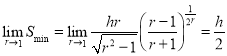 .
.
Таким образом, если скорость ракеты не больше скорости цели, то она не приблизится на расстояние меньшее, чем 0.5h.
Литература:
- Куркоткин В. И., Стерлигов В. Л. Самонаведение ракет. — М.: Воениздат, 1963. — 92 с.







