Задача тепло- имассообмена впористых оболочках свнутренним телом
Атамирзаев Махмуджан, доцент,
Юлдашев Нурилла Нигматович, доцент
Ташкентский институт инженеров ирригации и механизации сельского хозяйства (Узбекистан)
Многие задачи химической технологии, механики приводятся к задачам тепло- и массообмена в пористых средах. Например, к задачам такого типа можно отнести сушку кокона. При сушке кокон моделируется как пористая сферическая или цилиндрическая оболочка с внутренним телом (куколка). В статье предлагается математическая модель сушки кокона.
Процесс сушки кокона можно условно разделить на два этапа. На первом этапе за счет нагрева увеличивается давление газа в наружной области кокона. Происходит фильтрация нагретого воздуха вовнутрь кокона и заодно нагревается кокон. Из-за теплопередачи и фильтрации нагретого воздуха воздух внутри кокона и куколка нагреваются. Нагрев куколки продолжается таким образом до достижения ею температуры кипения воды Ткип. При достижении Ткук=Ткип начинается второй — более сложный этап тепло- и массообмена, так как начинается испарение. Полагая постоянство температуры куколки, так как идет испарение, можно определить скорость испарения. Далее идет обратная фильтрация: с увеличением концентрации газа внутри кокона увеличивается давление смеси. Это приводит к выходу смеси воздуха и водяного пара из кокона. После определенного времени устанавливается режим, когда образуются однородные температурное и барическое поля.
Сформулируем задачи по этапам.
Положим, что поверхности кокона и куколки образуют концентрические сферы. Куколка имеет радиус Rкл, внутренний и внешний радиусы кокона составляют Rкв и Rкн. Введем также условный радиус Ry, который отражает не занятое коконами пространство воздуха Vвоз (рис. 1):
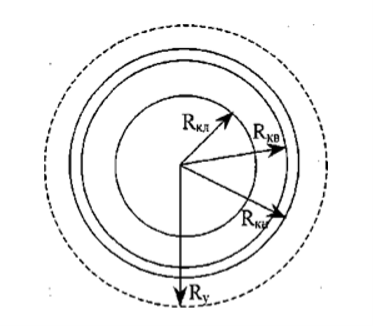
Рис. 1. Геометрическая интерпретация предполагаемой облас-ти сложного тепло-массообмена.
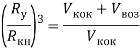 (1)
(1)
где ![]() — объем, занятый коконами в сушилке;
— объем, занятый коконами в сушилке; ![]() — объем сушки.
— объем сушки.
Полагаем, что объем закрыт. То есть тепло- и массообмен между сушилкой и окружающей средой отсутствуют.
В начальный момент все пространство ![]() имеет одинаковую температуру Т0. Воздух имеет нулевую скорость
имеет одинаковую температуру Т0. Воздух имеет нулевую скорость ![]() , плотность
, плотность![]() и давление Р0. Плотность куколки составляет
и давление Р0. Плотность куколки составляет ![]() .
.
С момента времени t = 0 на поверхности r = Ry устанавливается температура Ту = const. Так как через эту поверхность отсутствует массообмен, то![]() , с = 1. Здесь и далее с — массовая концентрация воздуха в смеси (воздух + пар воды).
, с = 1. Здесь и далее с — массовая концентрация воздуха в смеси (воздух + пар воды).
В наружной области кокона скорость давления движение, и температура чистого воздуха описываются уравнениями [2]:
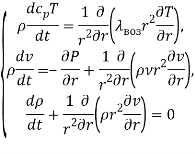 (2)
(2)
Здесь ![]() — коэффициент теплопроводности воздуха (в целом, смеси воздуха и водяного пара),
— коэффициент теплопроводности воздуха (в целом, смеси воздуха и водяного пара), ![]() — кинематическая вязкость воздуха,
— кинематическая вязкость воздуха,![]() — приведенная изобарическая теплоемкость воздуха.
— приведенная изобарическая теплоемкость воздуха.
Уравнение состояния воздуха описывается зависимостью
![]() (3)
(3)
Здесь и далее полагаем, что ![]() ,
, ![]() и
и ![]() имеют постоянные значения.
имеют постоянные значения.
Увеличение температуры газа в наружной области приводит к увеличению давления. В наружной и внутренней поверхностях оболочки кокона давление имеет разные значения Ркн и Ркв. Благодаря их разности воздух начинает просачиваться через оболочки кокона со скоростью [1]:
![]() (4)
(4)
где ![]() — коэффициент фильтрации оболочки кокона.
— коэффициент фильтрации оболочки кокона.
Так как Ркв<Ркн, то uf имеет отрицательное значение в начальной стадии сушки.
Теплообмен газа с коконом имеет идеальный случай интенсивности. С одной стороны имеет место теплообмен газа с поверхностью кокона, с другой стороны просачивающийся воздух обогревает тонкие нитки, которые практически моментально приобретают температуру воздуха.
В связи с этим можно принимать равными температур газа и оболочки в фиксированном слое и в заданное время. С учетом постоянного значения пористости скелета ![]() закон сохранения и переноса энергии в газе описывается уравнением в вида:
закон сохранения и переноса энергии в газе описывается уравнением в вида:
![]() ,(5)
,(5)
где q– количествотепла, предаваемое от газа в скелет оболочки за единицы времени в единичном объеме. Соответствующее уравнение для скелета оболочки имеет вид:
![]() ,(6)
,(6)
где индексом “ск” выделены параметры скелета оболочки кокона.
По членным суммированием последних двух уравнений получим одно-температурную модель теплообмена в оболочке кокона:
Пологая, что ![]() из (4) отражает скорости газа в наружной сфере оболочки кокона,
из (4) отражает скорости газа в наружной сфере оболочки кокона, ![]() определим в виде:
определим в виде:
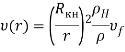 ,(8)
,(8)
который вытекает из грубой аппроксимации уравнения сохранения массы, где ![]() — плотность воздуха на верхней границе кокона, т. е. при
— плотность воздуха на верхней границе кокона, т. е. при ![]() .
.
Подобным образом скорости ![]() и
и ![]() служат граничными для скорости газа условиями во внешней и внутренней поверхностях оболочки кокона.
служат граничными для скорости газа условиями во внешней и внутренней поверхностях оболочки кокона.
Однозначность температуры газа на поверхностях оболочки достигается применением условий:
![]() ,
,![]() (9)
(9)
Которые обеспечивают также непрерывность распределения температуры в области расчета.
В полости между коконом и куколкой процессы переноса описываются уравнениями (2) и (3). В первом этапе сушки, когда испарение отсутствует, т. е. ![]() , на поверхности куколки скорость потока равняется нулю (здесь
, на поверхности куколки скорость потока равняется нулю (здесь ![]() — температура поверхности куколки;
— температура поверхности куколки; ![]() — температура кипения воды). Нагревание куколки происходит благодаря поверхностного теплообмена
— температура кипения воды). Нагревание куколки происходит благодаря поверхностного теплообмена
![]() ,(10)
,(10)
где индексом “кл”выделены параметры куколки.
Внутри куколки теплообмен описывается уравнением:
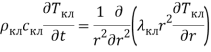 ,(11)
,(11)
которое реализуется совместно с условием симметрии в центре куколки:
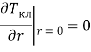 (12)
(12)
С достижением ![]() процесс усложняется, т. к. начинается испарение воды из куколки. Соответственно в уравнении (3)
процесс усложняется, т. к. начинается испарение воды из куколки. Соответственно в уравнении (3) ![]() следует заменить на:
следует заменить на:
![]() ,(13)
,(13)
где ![]() и
и ![]() – соответственно молярные массы воздуха и водяного пара. Аналогично в системе (2) следует ввести замены
– соответственно молярные массы воздуха и водяного пара. Аналогично в системе (2) следует ввести замены ![]() вместо
вместо ![]() ,
, ![]() на
на![]() , a
, a![]() на
на ![]() ,
,
где: ![]() — изобарическая теплоемкость воздуха;
— изобарическая теплоемкость воздуха; ![]() — изобарическая теплоемкость пара;
— изобарическая теплоемкость пара; ![]() — теплоемкость смеси (воздух+пар воды).
— теплоемкость смеси (воздух+пар воды).
В стадии испарения на поверхности куколки налагается условие
![]() .(14)
.(14)
Здесь![]() – плотность теплового потока, предаваемого газом
– плотность теплового потока, предаваемого газом
куколке;
где: ![]() — количество массы влаги выделяемая из куколки за единицу времени;
— количество массы влаги выделяемая из куколки за единицу времени; ![]() — поверхность куколки (
— поверхность куколки (![]() ).
).
На поверхности испарения скорость газа составляет:
![]() ,(15)
,(15)
где ![]() — плотность пара воды при температуре кипения при заданном давлении;
— плотность пара воды при температуре кипения при заданном давлении; ![]() — радиус куколки.
— радиус куколки.
Литература:
- Теория тепломассообмена: Учебник для вузов / С. И. Исаев и др.; Под ред. А. И. Леонтева. — М.: Высшая школа, 1979. — 495с.
- Продьяконов И. О., Люблинская И. Е., Рыжков А. Е. Гидродинамика и массообмен в дисперсных системах жидкость — твердое тело. — Л.:1987.







