В ![]() рассмотрено построение уравнения разветвления (УР) по допускаемой им группе. В основе примененного там метода лежит известная схема из теории инвариантов, изложенная в
рассмотрено построение уравнения разветвления (УР) по допускаемой им группе. В основе примененного там метода лежит известная схема из теории инвариантов, изложенная в ![]() . Здесь эта задача решается методами группового анализа дифференциальных уравнений
. Здесь эта задача решается методами группового анализа дифференциальных уравнений ![]() при значительно меньшем объеме вычислительной работы. Терминология и обозначения из теории ветвления решений нелинейных уравнений те же, что в
при значительно меньшем объеме вычислительной работы. Терминология и обозначения из теории ветвления решений нелинейных уравнений те же, что в ![]() .
.
УР ![]() допускает группу G (инвариантно относительно G), если для некоторых ее представлений
допускает группу G (инвариантно относительно G), если для некоторых ее представлений ![]() и
и ![]()
![]() (1)
(1)
Всюду ниже УР предполагается аналитическим, т. е. функции ![]() голоморфны в окрестности
голоморфны в окрестности ![]() . УР будем называть вещественным, если
. УР будем называть вещественным, если ![]() коммутирует с операцией
коммутирует с операцией ![]() комплексного сопряжения. Не будем явно указывать зависимость
комплексного сопряжения. Не будем явно указывать зависимость ![]() от параметра
от параметра ![]() , не являющуюся существенной для группового анализа. Поэтому следует считать, что коэффициенты построенных ниже систем разветвления являются аналитическими функциями малого параметра
, не являющуюся существенной для группового анализа. Поэтому следует считать, что коэффициенты построенных ниже систем разветвления являются аналитическими функциями малого параметра ![]() . Равенство (1) означает, что для рассматриваемой группы преобразований
. Равенство (1) означает, что для рассматриваемой группы преобразований
![]() (2)
(2)
многообразие ![]() в пространстве
в пространстве ![]() является инвариантным многообразием. Рассматривая
является инвариантным многообразием. Рассматривая ![]() — параметрическую группу преобразований (2), будем предполагать, что
— параметрическую группу преобразований (2), будем предполагать, что ![]() является неособым инвариантом многообразием, т. е. если
является неособым инвариантом многообразием, т. е. если ![]() — базис алгебры Ли группы (2), то ранг
— базис алгебры Ли группы (2), то ранг ![]() матрицы
матрицы ![]() ν
ν![]() (ν– номер строки, i, j — номера столбцов) на многообразии
(ν– номер строки, i, j — номера столбцов) на многообразии ![]() совпадает с ее общим рангом
совпадает с ее общим рангом ![]() . Если теперь
. Если теперь
![]() (3)
(3)
— базисная система функционального независимых инвариантов группы (2), то, согласно![]() , многообразие
, многообразие ![]() можно представить в виде
можно представить в виде![]() и для построения общего вида УР должно быть выполнено условие rank
и для построения общего вида УР должно быть выполнено условие rank  независимости системы (3) по отношению к переменным
независимости системы (3) по отношению к переменным ![]() . Это условие можно заменить требованием
. Это условие можно заменить требованием ![]()
![]() . Указанная схема построения инвариантных многообразий
. Указанная схема построения инвариантных многообразий ![]() приводит к понижению порядка (редукции) УР с помощью полной системы функционально независимых инвариантов
приводит к понижению порядка (редукции) УР с помощью полной системы функционально независимых инвариантов ![]() .
.
1. Группы SO (2) и O (2). Если УР ![]() допускает группу вращений
допускает группу вращений ![]() , то
, то
![]()
(далее будем использовать обозначение
Теорема. Двумерное УР, допускающее группу вращений SO (2), имеет вид
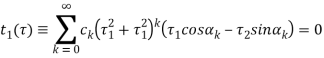 (4)
(4)
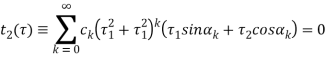
Если, кроме того, УР инвариантно относительно отражения ![]() , т. е. допускает группу O (2), то в (4)
, т. е. допускает группу O (2), то в (4) ![]() при всех k.
при всех k.
Действительно, инфинитезимальный оператор группы (2) имеет вид
![]() ,
,
а в полярных координатах
![]() ,
,
![]()
![]() , откуда
, откуда ![]() . Так как r*=1, то редуцированное с помощью системы инвариантов УР имеет вид
. Так как r*=1, то редуцированное с помощью системы инвариантов УР имеет вид ![]() , откуда следует
, откуда следует
![]() .
.
В силу аналитичности ![]() в окресности
в окресности ![]()

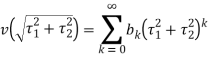
Полагая
 , получаем (4), где
, получаем (4), где ![]() . Инвариантность (4), относительно отражения J дает
. Инвариантность (4), относительно отражения J дает ![]() ,
,
Следствие. УР (4), допускающее группу SO (2), потенциально, т. е.
![]() , в том и только том случае, если оно, кроме того, инвариантно относительно отражения J.
, в том и только том случае, если оно, кроме того, инвариантно относительно отражения J.
Действительно, необходимое условие ![]() потенциальности векторного поля
потенциальности векторного поля ![]() дает
дает ![]() , т. е.
, т. е. ![]() . Если же, наоборот,
. Если же, наоборот, ![]() , то
, то

Для построения систем разветвления, допускающих кристаллографические группы, когда вещественное УР инвариантно относительно отражений, удобнее выполнить приведенные выше рассуждения в комплексных переменных
![]() ,(5)
,(5)
![]() .
.
Это поможет преодолеть технические трудности, связанные с учетом инвариантности УР относительно комплексного сопряжения. Тогда (см., например,![]() )
)
![]()
![]()
и, следовательно,
![]() . (6)
. (6)
Базис инвариантов можно выбрать в виде
![]() .
.
Тогда система разветвления (неособое инвариантное многообразие) запишется следующим образом:
![]() ,
,
или, в силу ее аналитичности по ![]() ––
––
 (7)
(7)
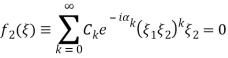
В соответствии с теоремой. Дополнительная симметрия относительно отражения
![]() дает
дает ![]() .
.
Литература:
- Логинов Б. В. Теория ветвления решений нелинейных уравнений в условиях групповой инвариантности. Ташкент: Фан, 1985. 184 с.
- Дьедонне Ж., Керрол Дж., Мамфорд Д. Геометрическая теория инвариантов. М.: Мир, 1974. 280 с.
- Овсянников Л. В. Групповой анализ дифференциальных уравнений. М.: Наука, 1978. 400 с.
- Овсянников Л. В. Лекции по теории групповых свойств дифференциальных уравнений. Новосибирск: Изд-во НГУ, 1966. 131 с.
- Ибрагимов Н. Х. Группы преобразований в математической физике. М.: Наука, 1983. 280 с.
- Вайнберг М. М.. Треногин В. А. Теория ветвления решений нелинейных уравнений. М.: Наука, 1969. 526 с.
- Гончар А. А., Шабат Б. В. Аналитическая функция. Аналитические функции нескольких комплексных переменных. Математическая энциклопедия. Е.1.М.: Советская энциклопедия. 1977. С.261–273.







