В методе неортогонального множественного доступа с разделением каналов по мощности PD-NOMA используется мощностной домен для разделения пользовательских каналов, которые при этом физически размещаются в едином частотно-временном ресурсе [1, с.1].
При неортогональном мультиплексировании помехой является смесь АБГШ и сигналов соседних каналов (системная помеха). Вывод общего аналитического выражения для расчета пропускной способности PD-NOMA каналов является невыполнимой задачей из-за отличия характеристик помехоустойчивости сигнально-кодовых конструкций. Поэтому, для упрощения, при расчете используется два допущения: 1) системная помеха мощностью P от соседних каналов представлена в виде нормальной помехи N идентичной мощностью; 2) паразитный канал демодулируется и компенсируется безошибочно. [2, с.30–100]. Соответственно, результат расчета является грубым и не позволяет получить точной расчет помехоустойчивости канала связи PD-NOMA. Для получения более точных результатов характеристик каналов связи при использовании конкретной сигнально-кодовой конструкции используется моделирование. Целью настоящей работы является сравнение помехоустойчивости, полученной в результате расчета и моделирования.
В многоканальной системе из K каналов с разделением по мощности PD (Power Division), одновременно использующих единую полосу частот F при известных парциальных мощностях в каналах p1…pK пропускная способность k-го канала определяется:![]()
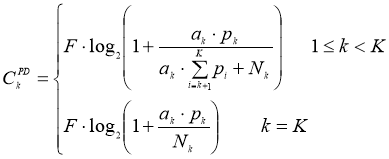 (1)
(1)
В каналах 1 ≤ k < K сумма парциальных мощностей Σpi каналов i < k является системной помехой для k-го канала, а в последнем K-ом канале при полном устранении системной помехи искажения вносит только АБГШ мощностью NK. Поэтому, выражение (1) справедливо в случае полного устранения системной помехи каналов верхнего уровня при (последовательной подавление помех) SIC-демодуляции [3, с.283]. На рисунке 1 представлена зависимость пропускной способности двух каналов PD-NOMA при безошибочной передачи данных от отношения сигнал/шум (SNR) для канала верхнего уровня (UE1) и канала нижнего уровня (UE2) при безошибочной демодуляции и компенсации канала верхнего уровня в дальнейшем (идеальный случай).
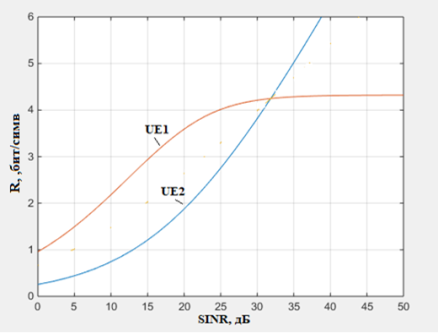
Рис. 1. Зависимость SINR(R) при безошибочной демодуляции и компенсации канала верхнего уровня
Условия моделирования приближены к условиям практической эксплуатации. В качестве помехи выступает канал нижнего уровня. Структурная схема модели приведена на рисунке 1.
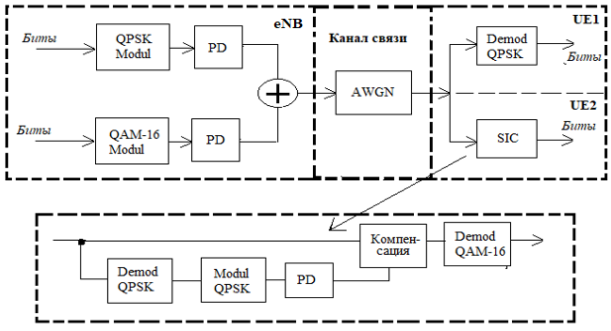
Рис. 2. Структурная схема модели
В качестве примера приведен результат моделирования для случая, когда для передачи данных в канале верхнего уровня UE1 используется QPSK-модуляция с парциальной мощностью каждого символа p1 = 0,95 Вт, а в канале нижнего уровня UE2 — QAM-16 с мощностью p2 = 0,05 Вт. Общая мощность P транспортного сигнала составляет P = 1 Вт. Характеристика помехоустойчивости измеряется для вероятности битовой ошибки 10–3. Пропускная способность первого абонента составляет 2 бит/с, а второго — 4 бит/с. На рисунке 3 представлена зависимость BER(SNR) для первого (UE1) и второго (UE2) абонентских каналов.
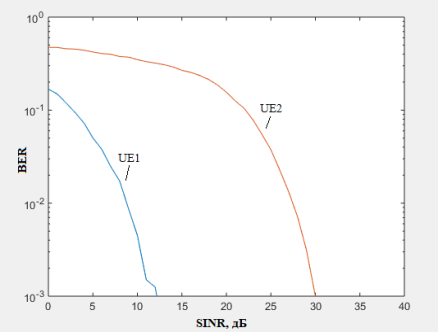
Рис. 3. Зависимость BER(SINR) при парциальных мощностях 0.95 и 0.05 Вт.
Используя второе допущение, были рассчитаны значения помехоустойчивости при BER = 10–3 используемых сигнально-кодовых конструкций (BPSK, QPSK, QAM-16), представленные в таблице 1.
Таблица 1
Результаты расчета
|
Пропускная способность |
Отношение сигнал\шум, дБ |
|
|
R, Бит/символ |
UE1 |
UE2 |
|
R = 1 |
10.3 |
22.8 |
|
R = 2 |
13.5 |
25.5 |
|
R = 4 |
27 |
33 |
Значения отношения сигнал/шум для различной пропускной способности в каналах верхнего и нижнего уровней из таблицы 1, показывают какую помехоустойчивость ожидается получить при моделировании. На рисунке 4 приведена зависимость помехоустойчивости обоих каналов от различных пропускных способностей для идеальной сигнально-кодовой конструкции и безошибочной передачи данных (где на рисунке UE1 и UE2) и для используемой сигнально-кодовой конструкции с вероятностью битовой ошибки 10–3 (где на рисунке (UE1) и (UE2)).
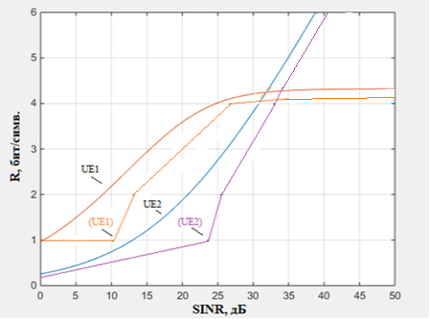
Рис. 4. Зависимость пропускной способности каналов от отношения сигнал/шум с вероятностью битовой ошибкой 10–3
Для сравнения рассчитанной и полученной при моделировании помехоустойчивости в таблице 2 приведены результаты моделирования для идентичных сигнально-кодовых конструкций при парциальных мощностях P = 0,95 для первого и P = 0,05 для второго каналов.
Таблица 2
Результаты моделирования
|
Скорость |
Отношение сигнал\шум, дБ |
|
|
R, Бит/символ |
UE1 |
UE2 |
|
R = 1 |
12 |
23 |
|
R = 2 |
11.5 |
28 |
|
R = 4 |
26 |
30 |
На рисунках 5 и 6 показаны точки, построенные по значениям из таблиц 1 и 2, где точки X представляют результат расчета, а (X) — результат моделирования для UE1 и UE2 соответственно.
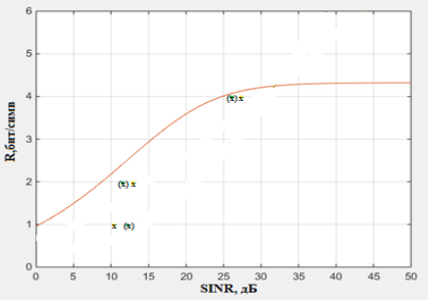
Рис. 5. Помехоустойчивость для канала верхнего уровня UE1
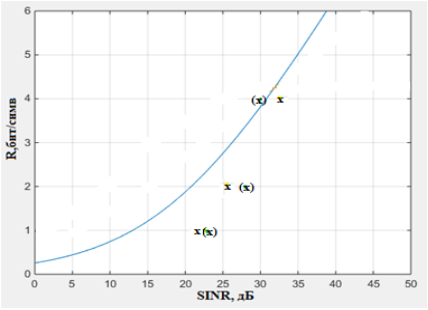
Рис. 6. Помехоустойчивость для канала нижнего уровня UE2
Величина ΔSINR показывает разницу помехоустойчивости каналов между расчетом и моделированием. Например, при скорости передачи R = 2 бит/симв., значение ΔSINR = 2 дБ, для канала верхнего уровня и ΔSINR = 2.5 дБ для канала нижнего уровня.
Таким образом, показано, что по теореме Шеннона можно грубо оценить помехоустойчивость в каналах PD-NPOMA. При этом, среднее различие между результатами расчета и моделирования составляет 2 дБ. Поэтому, для более точной оценки помехоустойчивости каналов связи PD-NOMA с использованием конкретной сигнально-кодовой конструкции требуется проводить моделирование при различных соотношениях парциальных мощностей.
Литература:
- Benjebbour A. Concept and practical considerations of non-orthogonal multiple access (NOMA) for future radio access / A. Benjebbour, Y. Saito, Y. Kishiyama, A. Li, A. Harada, T. Nakamura // Proc. Int. Symp. Intelligent Signal Process. Commun. Syst. (ISPACS). — 2013. — PP. 770–774.
- Крюков Я. В. Формирование и обработка сигналов моноканальных систем связи с разделением каналов по мощности // ТУСУР. 2017. С. 31–100.
- D. Tse, P. Viswanath, Fundamentals of Wireless Communication // Cambridge. — The UK: Cambridge University Press. — 2005.







