The value of the computational experiment can not be overestimated, especially if the field experiment is dangerous, expensive or simply impossible. Only a reasonable combination of analytical and numerical methods is a necessary condition for success in solving practical problems. Therefore, it is necessary to create reliable methods for calculating the load-bearing elements of thin-walled structures.
The paper is devoted to numerical modeling and automation of the solution of boundary value problems for viscoelastic plates of arbitrary configuration for various models of viscosity in a Maple system environment.
As is known, the mathematical model of this problem has the form:
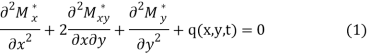
Note that if we use the hypothesis of the constancy of the Poisson's ratio when formulating the basic physical relationships, then the bending and twisting moments are calculated by the following formulas:

![]()
where D is the stiffness of viscoelastic plates; ![]() integral operator with relaxation kernels R(t), т. е.
integral operator with relaxation kernels R(t), т. е. 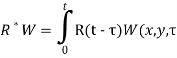 )d
)d![]() — deflection plate;
— deflection plate;
µ — Poisson's ratio; q (x, y, t) is the intensity of the external load.
If, on the other hand, we use the hypothesis of the elasticity of volume deformations, then for bending and twisting moments it is calculated by the following formulas
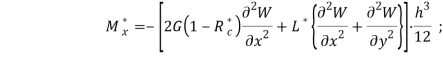
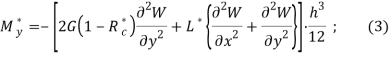
![]()
where G=E/2(1+µ) — shear modulus; E — elastic modulus; ![]() — integral operator with shear relaxation kernels
— integral operator with shear relaxation kernels ![]()
![]() — integral operator, i.e.
— integral operator, i.e. ![]()
K=E/3(1- 2µ) — bulk modulus of elasticity; h — is the thickness of the plate.
As is known, the equation of an oscillating thin viscoelastic plate has the form
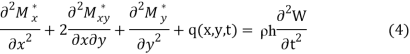
where ρh — the mass of the slab per unit surface.
Equations (4) are solved for the corresponding boundary and initial conditions
![]()
where ![]() — differential operators that depend on the boundary conditions; Г — boundary of the region;
— differential operators that depend on the boundary conditions; Г — boundary of the region; ![]() и
и ![]() — initial values.
— initial values.
Solutions of equations (1) and (4) are sought in the form
W(x,y,t)=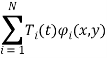 (6)
(6)
where ![]() - systems of coordinate functions (Chebyshev polynomials, power, trigonometric, Schoenberg splines, etc.) SКF.
- systems of coordinate functions (Chebyshev polynomials, power, trigonometric, Schoenberg splines, etc.) SКF.
Note that SКF exactly satisfy all the boundary conditions that are constructed using the Rvachev R-functions method [1];
![]() — unknown time functions t.
— unknown time functions t.
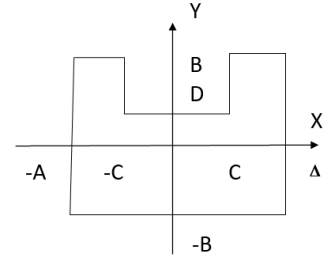
Fig. 1.
First, let us consider the problems of quasistatic bending of the freely supported viscoelastic plates shown in Fig. 1. Let the plate be subjected to a load (q = 1). The nucleus of shear relaxation is the nucleus R(t)=ε![]() .
.
In order to solve the problem numerically, we use the structure
W(x,y)= ωΦ1- ω2 /2∙ [Φ1(D2ω+μТ2ω)+2D1Φ1 — ωΦ2] (7)
In the above structural formulas, Ф1 and Ф2 are undefined components of the structure, which are represented in the form
Фs=
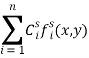 ,
, The presence of two or more numbers of undefined functions in the structure creates difficulties in solving boundary value problems. We take one of the undefined functions equal to zero. For example, in (7) we set
Ф1 ≠ 0 и Ф2=0, but can not Ф2 ≠ 0 и Ф1=0, since this circumstance leads to the appearance of an «extra» boundary condition [1].
The normalized equation of the geometry of the region for the plate shown in Fig. 1 has the form:
Ω=((Ω 1 ![]() (-Ω 2)) (8)
(-Ω 2)) (8)
where Ω 1 =(a2-x2)/2a ![]() (b2-y2)/2b, Ω 2 =(c2-x2)/2c
(b2-y2)/2b, Ω 2 =(c2-x2)/2c ![]() (y-d)
(y-d)
![]() — logical conjunction operator of zero order.
— logical conjunction operator of zero order.
Note that, when solving boundary value problems, an orthonormal SКF is used for the biharmonic and unit operator, respectively, and then a numerical method based on the use of quadrature formulas is used to solve the autonomous systems of integral and integro-differential equations [2].
Figure 2a shows the change in the deflection W (x, y, t) in time (dashed line) along the axis OX and y = 0.2, and in Fig. 2b — the variation of the bending ![]() and the torque
and the torque ![]() (dashed line) in the same point. The solid lines show the variation of the same values for a plate with a constant Poisson's coefficient and a relaxation nucleus coinciding with the nucleus Rc (t) for the plate under consideration.
(dashed line) in the same point. The solid lines show the variation of the same values for a plate with a constant Poisson's coefficient and a relaxation nucleus coinciding with the nucleus Rc (t) for the plate under consideration.
Note that when the hypothesis of the constancy of the Poisson's ratio is used, then the deflection does not change with time t. The numerical results show that the results obtained on the basis of the hypothesis of the elasticity of volume deformations are in good agreement with the experimental results. Here we compared the results obtained on the basis of two hypotheses.
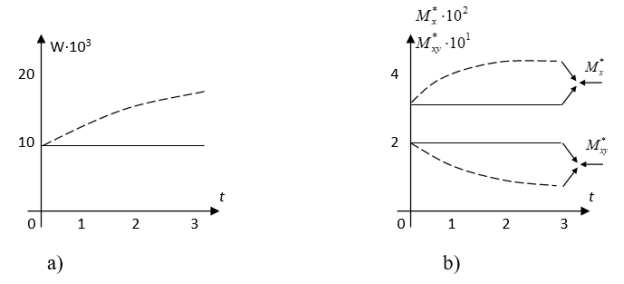
Fig. 2
The results are obtained for the following values of the dimensionless parameters:
Λ=a/b=1; c/a=0.5; d/a=0.2; ε=0.05; β=0.075; µ=0.17
Next, we consider forced oscillations of rigidly clamped viscoelastic plates (Fig. 1). Let the plate be subjected to a load (q = 1) and under the following initial conditions W|t=0=0, Wt|t=0=0.
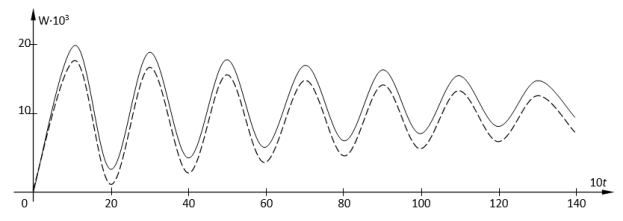
Fig. 3
The results are obtained for the following values of the dimensionless parameters:
Λ=a/b=1; c/a=0.5; d/a=0.2; ε=0.05; β=0.075; µ=0.17
Figure 3 shows the change in the deflection of the plate W (0.0; 0.2; t) obtained on the basis of two hypotheses. For comparison, solid lines indicate the change in the deflection of the plate W (0.0; 0.2; t), obtained on the basis of the hypothesis of the constancy of the Poisson's ratio.
In Table 1, for c / a = 0.5; d / a = 0.5, the values of the frequency parameter λi of the first three tones of oscillations of elastic plates obtained with the help of a power polynomial are given. The corresponding values of the frequency parameter wi are determined by the formula wi=λi/a2√D/ρh.
The number of SКF ranged from 15 to 36, with good convergence of numbers λi.
Table 1
|
λi |
N=15 |
N=21 |
N=28 |
N=36 |
|
λ1 |
10.115 |
8.562 |
8.265 |
7.922 |
|
λ2 |
19.272 |
18.013 |
16.284 |
16.127 |
|
λ3 |
27.822 |
26.717 |
22.312. |
21.531 |
The R-function method makes it possible to construct coordinate sequences for regions of practically arbitrary configuration and boundary conditions of complex type. An effective computational algorithm for calculating the problems of the hereditary theory of viscoelasticity with a complicated shape of the boundary is constructed on the basis of a combination of methods of R-function and variational methods [3]. Based on the proposed computational algorithm, a smart algorithmic system was developed.
With the help of the developed intellectual algorithmic system, it is possible to solve operatively the whole class of problems of mechanics of a deformable solid and it can easily be generalized for other classes of problems in mathematical physics.
References:
- Rvachev V.L, Kurpa L. V. R-functions in problems of the theory of plates. Kiev: Naukova dumka.1987.176 p.
- Badalov F. B. Methods for solving integral and integro-differential equations of the hereditary theory of viscoelasticity. Tashkent. Mekhnat.1987.289 p.
- Nazirov Sh.A., Sadikov Kh.S. Complex of software for solving boundary value problems by variational methods. / Algorithms. Tashkent: RISO AN Uz. 65.1988.







