Расчетное исследование влияния типа конечных элементов на коэффициент запаса топологически оптимизированной конструкции



Расчетное исследование влияния типа конечных элементов на коэффициент запаса топологически оптимизированной конструкции

Федосеев Николай Владимирович, студент;

Семёнов Сергей Валерьевич, ассистент

Пермский национальный исследовательский политехнический университет

Данная статья посвящена методу топологической оптимизации, который позволяет увеличить удельную прочность конструкции путем изменения её геометрии. В работе приведены теоретические основы топологической оптимизации, а также области применения этого метода. Кроме этого, в статье были исследованы на практике два типа оптимизации одной и той же конструкции: с линейными элементами и параболическими. Расчет на статическую нагрузку обоих оптимизированных конструкций и последующее их сравнение дало возможность выявить лучший тип оптимизации.

Ключевые слова: топологическая оптимизация, конечно-элементная модель, линейный тип элементов, параболический тип элементов, коэффициенты запаса.

Введение

Развитие вычислительных методов и технологий производства позволяет создавать все более легкие и прочные детали. Наиболее бурное развитие данные вычислительные методы получили вместе со значительным увеличением мощности компьютеров. С их помощью появилась возможность более точно прогнозировать поведение конструктивных элементов под нагрузкой и более оптимально подбирать геометрические параметры конструкции, снижая, таким образом, к примеру, массу детали и обеспечивая при этом максимум жесткости и прочности [1].

В последнее время особую популярность получили аддитивные технологии, обеспечивающие практически полную свободу формы детали, которая может быть изготовлена как из пластика, так и из металла. Основным преимуществом данных технологий является технологическая простота, а недостатками — время производства (значительно большее в сравнении с традиционными субтрактивными технологиями) и ограничение размеров детали (хотя существуют технологии, к примеру, с использованием методов плазменного наплавления, позволяющие обходить данное ограничение [2]).

Уменьшение веса деталей особенно приветствуется в авиационной промышленности, так как оно позволяет значительно улучшить эксплуатационные характеристики летательных аппаратов. К примеру, в случае самолетов это может быть увеличение полезной нагрузки, а в случае дронов — возможность добавления новых функциональных элементов [3]. Уменьшение веса элементов может быть полезно и для других производственных отраслей — автомобильной промышленности, к примеру.

Одним из методов, получивших наибольшую популярность в решении задач, связанных с уменьшением массы деталей, является метод топологической оптимизации.

Основы топологической оптимизации

Топологическая оптимизация (ТО) — это численный метод, который позволяет изменять структуру детали таким образом, чтобы удалить из нее ненагруженные части. Следовательно, данный метод может быть использован для уменьшения массы детали. Рассмотрим данный метод на основе следующей задачи — максимизации жесткости оптимизируемой детали. В основе ТО лежит обычная оптимизационная задача, поэтому все начинается с записи целевой функции [3]. Для определения нагрузок и граничных условий была выбрана опорная область, и в качестве задачи нахождение оптимального выбора значения жесткости E_ijkl(x), который является переменным по всей области. Если введена 2-линейная форма энергии a (т. е. внутренняя работа упругого тела в равновесной ситуации u для произвольного виртуального перемещения v), также называемая критерием соответствия, наряду с линейной формой деформации ε и нагрузкой l. [4]:

задача минимизации деформации (максимальной глобальной жесткости) принимает вид:

Другими словами, речь идет о получении конструкции, в которой будет наименьшая деформация при предполагаемой нагрузке. Уравнение равновесия записано в простой, вариативной форме, где U — кинематически допустимое поле смещения, f-сила, приложенная внутри тела, t-сила, приложенная на периферии области. Индекс E указывает на то, что 2-линейная форма энергии зависит от расчетных переменных, а E_ad является допустимым значением жесткости для данной задачи [4].

Для решения задачи с помощью численных методов типичным подходом является дискретизация модели с использованием метода конечных элементов. Следует отметить, что в интересующей области есть два поля: поле смещения u и поле жесткости E. используя одну и ту же сетку конечных элементов для двух полей и предполагая, что E постоянен в каждом элементе, можно записать дискретную форму задачи как:

где: u и f являются векторами смещения и нагрузок соответственно.

Матрица жесткости K зависит от жесткости E в пронумерованном элементе e = 1,..., N. тогда K можно записать в виде:

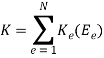
где: K_{e —} матрица жесткости элемента [4].

Из предложенных выше выражений следует, что на качество решения оптимизационной задачи напрямую влияет точность определения матриц жесткостей. В таком случае можно предположить, что использование параболических конечных элементов будет давать более точный результат при определении матриц жесткостей, чем при использовании линейных элементов. Проверим данную гипотезу на примере решения задачи топологической оптимизации кронштейна. В качестве критерия оценки качества оптимизации предлагается использовать коэффициент запаса прочности — чем он выше при одинаковом уменьшении массы, тем более удачная конфигурация конструкции была получена в результате оптимизации. Коэффициент запаса — величина, показывающая способность конструкции выдерживать прилагаемые к ней нагрузки выше расчётных [5]. Расчет конструкции осуществляется в пакете Autodesk Fusion 360.

Методика расчетного исследования

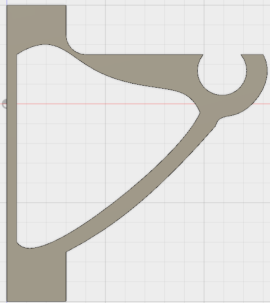
Имеется некоторая пластиковая (ABS пластик) конструкция, использующаяся как элемент подвеса (кронштейн). Плотность детали 0,001 гр/см³.

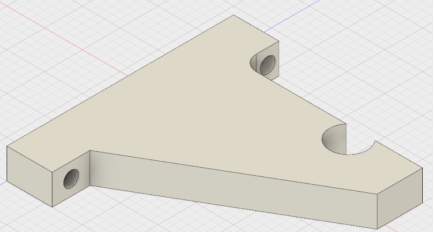
Рис. 1. Конструкция оптимизируемой детали

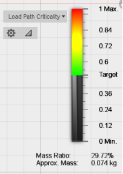
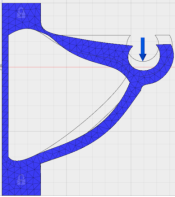
Определим запас прочности данной детали. Для этого, осуществим статический расчет данной конструкции на изгиб, закрепив ее по отверстиям на левой грани и приложив усилие в 50 Н на крючок.

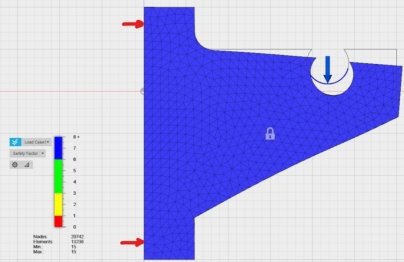
Рис. 2. Статический расчет коэффициента прочности кронштейна

Как видно из статического расчета, для данной конструкции запас прочности получился >15, что говорит о том, что прочность данной конструкции для данного типа нагружения избыточна.

Подвергнем данную конструкцию топологической оптимизации. Задача топологической оптимизации состоит в минимизации массы (на 30 %) и максимизации жесткости, при ограничениях в виде граничных условий и условий нагрузки. Так же в приоритете стоит максимальное достижение в конструкции состояния равнопрочности [6].

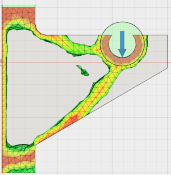
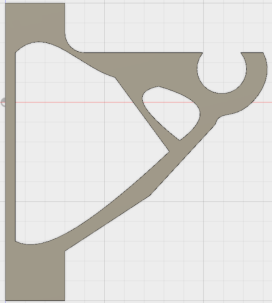
Для данной процедуры критически важны параметры сетки. Было предложено использовать два варианта: с линейными элементами и параболическими (Рис. 3а, 3б). Размер элемента одинаков и составляет — 5 мм.

а)	б)
Рис. 3. Результаты топологической оптимизации конструкции с линейными элементами (а) и параболическими (б)

Как видно из рис.3, для одинакового условия в 30 % уменьшении массы для разного типа элементов конструкции получились разными.

Далее полученные детали были обрисованы с учетом результатов оптимизации. Внешний контур детали обрисовывается максимально одинаковым образом, а внутренний — следуя логике оптимизированной детали.

а)	б)
Рис. 4. Детали, полученные в результате топологической оптимизации с линейными (а) и параболическими элементами (б)

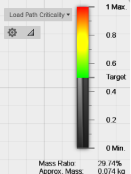
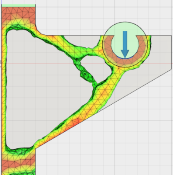
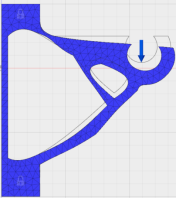
Производим расчеты статической нагрузки для полученных оптимизированных конструкций.

а)	б)
Рис. 5. Статический расчет коэффициента запаса прочности конструкции с линейными (а) и параболическими элементами (б)

Как видно из расчетов минимальный запас прочности конструкции с параболическими элементами (13,03) больше, чем у конструкции с линейными элементами (10,27), т. е. использование параболических элементов позволило получить нам более высокие коэффициенты запаса при одинаковом уменьшении массы.

Заключение.

В данной работе была затронута тема топологической оптимизации, как метода определения наилучшей формы детали, которая бы обладала наибольшей жесткостью при ограничениях в массе и объеме.

Также были подвергнуты сравнению два типа топологической оптимизации: с линейными и параболическими элементами. В ходе сравнения были произведены расчеты, которые показали, что при одинаковом уменьшении массы лучший результат был получен для задачи, решаемой с помощью конечных элементов более высокого порядка.

Литература:

1. Huang X., Xie M. Y. Evolutionary Topology Optimization of Continuum Structures: Methods and Applications. —iss. 1.— Hoboken: John Wiley & Sons, 2010. — 237 с.
2. Мост MX3D // MX3D. URL: http://mx3d.com/projects/bridge (дата обращения: 18.05.2018).
3. К. А. Башин, Р. А. Торсунов, С. В. Семенов. Методы топологической оптимизации конструкций, применяющиеся в аэрокосмической отрасли // Вестник ПНИПУ. Аэрокосмическая техника.. — Пермь: Пермский национальный исследовательский политехнический университет, Пермь, Россия, 2017.
4. Bendsoe M. P., Sigmund O. “Topology Optimization: Theory, Methods and Applications”.. — iss. 2. — Berlin: Springer-Verlag Berlin Heidelberg, 2004. — 370 с.
5. Коэффициент запаса // Википедия. URL: https://ru.wikipedia.org/wiki/Коэффициент_запаса (дата обращения: 18.05.2018).
6. Брюхова К. С., Максимов П. В. Алгоритм топологической оптимизации на основе метода ESO // Международный научно-исследовательский журнал. — Екатеринбург: Индивидуальный предприниматель Соколова Марина Владимировна, 2016. — С. 16–18.