Оптимизация распределения активной нагрузки энергосистемы между ТЭС и ГЭС с использованием программа MATLAB

В работе исследованы оптимальное распределение активной нагрузки энергосистемы между гидравлическими и тепловыми электростанциями с использованием программного комплекса Маtlab. Рассмотрен пример оптимального покрытия графика нагрузки энергосистемы всех суточных интервалов, обеспечивающих минимальный расход топлива.

Ключевые слова: энергосистема, электростанция, оптимизация, расход топлива, расход воды, график нагрузки, программирование.

В задаче краткосрочного оптимального планирования режимов гидротепловых энергосистем вместе с тепловыми электростанциями (ТЭС) расчетными станциями являются также гидроэлектростанции (ГЭС), имеющие водохранилища с регулированием расхода воды и, соответственно, мощности в рассматриваемом периоде. ГЭС, работающие на бытовом расходе рек, мощности которых определяются текущими притоками воды, заменяются соответствующими отрицательными нагрузками и не участвуют в оптимизационном процессе [1–3].

В тех случаях, когда режимы работы энергосистемы в отдельные моменты времени независимы друг от друга, задача оптимизации ее режима за цикл регулирования сводится к последовательной оптимизации режима для коротких интервалов (моментов) времени, например, для каждого часа суточного цикла регулирования, в отдельности. Задача оптимизации значительно усложняется в тех случаях, когда необходимо вводить условия, определяющие связь между режимами в отдельных интервалах времени. Такая связь возникает при наличии в энергосистеме электростанций с ограниченными запасами энергоресурсов, в частности ГЭС с водохранилищами и заданными расходами воды за цикл регулирования [2].

Условие баланса мощностей в энергосистеме без учёта потерь активной мощности в сети запишется как

W = P_T + P_Г — Р_С,

где P_T, P_Г, Р_С — соответственно активные мощности ТЭС, ГЭС и нагрузки ЭЭС.

Для ГЭС с суточным циклом регулирования сумма часовых расходов воды Q^(t) за сутки должна быть равна заданному суточному притоку воды Q_{сут.прит.} к водохранилищу.

.

Для определения минимума расхода условного топлива на генерируемые ТЭС и ГЭС при условии соблюдения баланса активных мощностей в сети и притока воды на ГЭС составляется функция Лагранжа в виде:

и, берутся частные производные от неё, приравняя их к нулю:

,

,

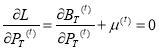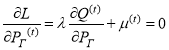где

.

Отсюда

.

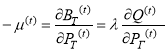Тогда критерием оптимального распределения активной нагрузки энергосистемы между ТЭС и ГЭС является:

.

Величина  носит название коэффициента Лагранжа и показывает какому количеству сэкономленного топлива ΔВ соответствует увеличение на 1 м³ пропускаемого через турбину ГЭС объёма воды. Таким образом, ГЭС сводится к разряду ТЭС. Значение  остаётся постоянным для всех расчётных часов.

Задавшись некоторым достоверным значением  и умножив его на характеристику относительных приростов (ХОП) расхода воды ГЭС, осуществляется распределение графика нагрузки энергосистемы между ТЭС и ГЭС. Затем, опираясь на полученные мощности ГЭС, определяются часовые расходы воды Q^(t), сумма которых даёт суточный расход Q_сут.

Если при этом заданный суточный расход воды ГЭС Q_зад равен расчетному Q_сут с достаточной точностью , то дальнейшая коррекция не производится. В противном случае значение  изменяется последовательно в большую сторону, если Q_сут. > Q_зад, и в меньшую сторону, если Q_сут. < Q_зад.

На основе полученного вывода разработан программный комплекс на базе Маtlab. Программа составлена для оптимального распределения графиков суммарных активных нагрузок энергосистемы между тепловыми и гидроэлектростанциями. Она позволяет определить оптимальные графики нагрузок всех электростанций, участвующих в оптимизации, с учетом технологических ограничений. Программа предусматривает выполнения оптимизации в условиях наличия в энергосистеме множества тепловых и гидроэлектростанций. Она дает возможность определить оптимальные режимы электростанций и энергосистемы с высокой точностью и надежностью [4].

Эффективность алгоритма, данного предложенного программного комплекса исследован на примере в оптимальном покрытии суммарного графика нагрузки энергосистемы (табл. 1) за цикл регулирования, состоящий из четырёх интервалов, одним ТЭС и ГЭС со следующими исходными данными:

1. Расходные характеристики эквивалентных ТЭС и ГЭС, заданные в виде полиномов второй степени:

;

.

2. Суточный расход воды на ГЭС .
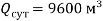3. Регулировочный диапазон электростанций:

Таблица 1

Суммарный график нагрузки энергосистемы.

Ниже приводится результаты данного исследования, полученные в программном комплексе Маtlab.

Рн= [430,000 650,000 820,000 490,000]

Оптимальные значения относительных приростов для каждого интервала нагрузки:

b_opt = [1,880 2,750 3,420 2,120]

Оптимальное значение выработки мощности ГЭС для каждого часа нагрузки:

Р_oпт = [149,492 225,613 284,235 170,491]

Оптимальное значение выработки мощности ТЭС для каждого часа нагрузки:

Р_oпт = [280,000 425,000 536,667 320,000]

Значения расхода топлива на ТЭС для каждого часа интервала:

B_расх = [391,200 726,875 1071,367 471,200]

Значения расхода воды на ГЭС для каждого часа интервала:

Заданное значение расхода воды для ГЭС [м³]:

Q_зад = 9600,000

Расчетное значение расхода воды для ГЭС [м³]:

Q_расчет = 9600,003

Значение λ удовлетворяющее условию заданного расхода воды:

λ = 1,143.

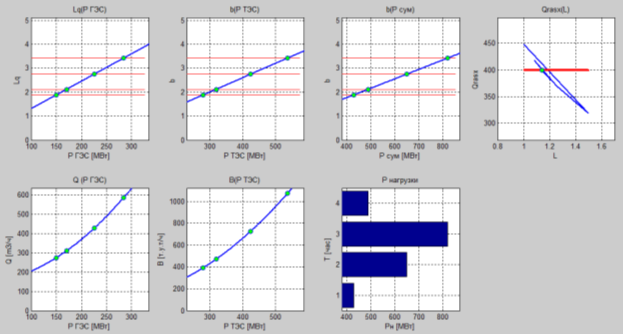
Рис. 1. Результаты расчета в программе Маtlab.

Полученные результаты с высокой точностью совпадают с результатами, полученными методом равенства относительных приростов расхода топлива (ОПРТ) (табл. 2).

Таблица 2

Окончательное значение

Максимальный небаланс воды

Расход топлива на ТЭС за сутки

Вывод:

Данная программа может быть использована диспетчерскими пунктами энергосистем для оптимального управления их режимами, также при проведении лабораторных и практических занятий по курсам «Электрические сети и системы», «АСУ и оптимизация режимов электрических станций и систем».

Литература:

1. Фазылов Х. Ф., Насыров Т. Х. Установившиеся режимы электроэнергетических систем и их оптимизация. –Т.: Молия, 1999.
2. Гайибов Т. Ш. Алгоритм оптимизации краткосрочных режимов гидротепловых энергосистем кусочно-линейной аппроксимацией нелинейных зависимостей. Электрика, 2009, № 4, с. 26–30.
3. Автоматизация диспетчерского управления в электроэнергетике/ Под общей ред. Ю. Н. Руденко и В. А. Семенова. — М.: Изд-во МЭИ, 2000.-648 с.
4. Гайибов Т. Ш., Реймов К. М. Программа «TESGES» для оптимального покрытия графиков нагрузок энергосистемы тепловыми и гидравлическими электрическими станциями. /Программа для ЭВМ/ № DGU 03033. 10.02.2015 г. Агентство по интеллектуальной собственности Республики Узбекистан.