![]()
Упругий цилиндр с радиальной трещиной является предельным случаем клина с углом ![]() [1]. Основные уравнения движения упругой среды, занимающей область В, задаются тремя группами соотношений:
[1]. Основные уравнения движения упругой среды, занимающей область В, задаются тремя группами соотношений:
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
Здесь тильдой обозначена операция транспонирования квадратной матрицы; ![]() -единичный тензор второго ранга; модули упругости, называемые постоянными Ламе. Здесь
-единичный тензор второго ранга; модули упругости, называемые постоянными Ламе. Здесь ![]() и
и ![]() — комплексные величины. Если
— комплексные величины. Если ![]() , тогда
, тогда ![]() и
и ![]() - действительные числа (постоянная Ламе). В цилиндрической системе координат уравнения (1), (2), (3) имеют вид
- действительные числа (постоянная Ламе). В цилиндрической системе координат уравнения (1), (2), (3) имеют вид
![]()
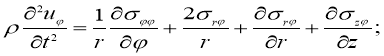 (4)
(4)
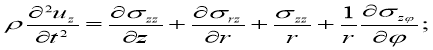
![]()
![]()
![]()
![]()
![]()
![]() (6)
(6)
![]()
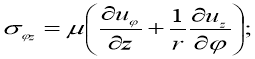
![]()
Где ![]() - соответсвенно компоненты тензора напряжений;
- соответсвенно компоненты тензора напряжений; ![]() -соответственно компоненты тензора деформаций. Связь между напряжением и деформацией приведена во второй главе (6). Соотношения (4), (5), (6) после тождественных алгебраических преобразований приводятся к системе шести дифференциальных уравнений, решенных относительно первой производной по радиальной координате
-соответственно компоненты тензора деформаций. Связь между напряжением и деформацией приведена во второй главе (6). Соотношения (4), (5), (6) после тождественных алгебраических преобразований приводятся к системе шести дифференциальных уравнений, решенных относительно первой производной по радиальной координате
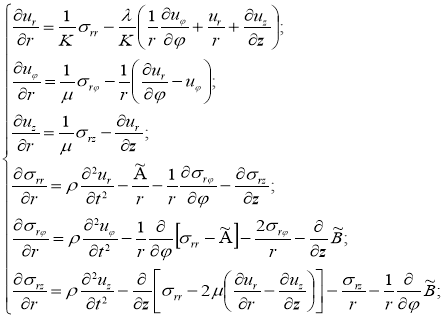 (7)
(7)
где введены обозначения
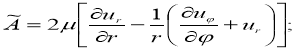
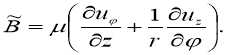
Краевые условия задаем в виде:
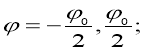
![]() (8)
(8)
Условия периодичности позволяют исключить зависимость основных неизвестных от времени и осевой координаты z с помощью следующей замены переменных:
![]()
![]()
![]() (9)
(9)
![]()
![]()
При условии (8) разделение переменных r и φ невозможно. С учетом (9) система уравнений (7) принимает вид:
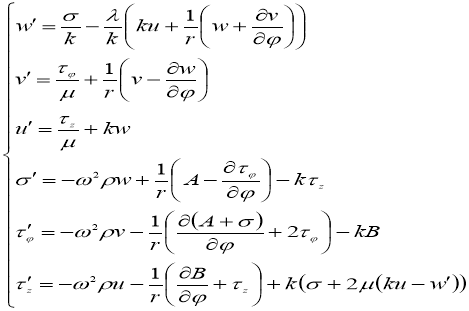 (10)
(10)
где 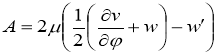
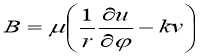
Аналогично преобразуются краевые условия (8)
![]()
![]() . (11)
. (11)
Нетрудно видеть, что компоненты тензора напряжения
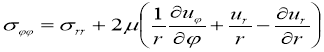 ,
, 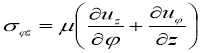 (12)
(12)
![]()
Тогда с учетом первого уравнения системы (12), краевые условия (11) принимают вид:
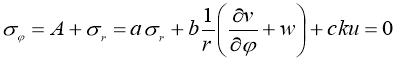
![]()
![]() (13)
(13)
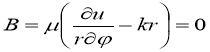
где
![]()
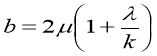
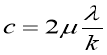
Краевая задача для системы уравнений в частотных производных выражена в выражении (13), система дифференциальных уравнений с помощью метода прямых позволит использовать в решении программный аппарат метода ортогональной прогонки. Согласно методу прямых прямоугольная область определения функции основных неизвестных покрывается прямыми, параллельными оси r и равномерно отстоящими друг от друга (рис.1).
Решение ищется только на этих прямых, а производная по направлению φ заменяется приближенными конечными разностями. Используемые аппроксимирующие формулы второго порядка для первой и второй производной имеют вид:
![]() (15)
(15)
![]() где i изменяется от 0 до
где i изменяется от 0 до ![]() ,
,![]() — проекция неизвестной функции напрямую с номером i; Δ — шаг разбиения по координате φ
— проекция неизвестной функции напрямую с номером i; Δ — шаг разбиения по координате φ
В результате дискретизации вектор основных неизвестных общей размерности 6N может быть записан в виде:
![]()
![]() (16)
(16)
Таким образом исходная спектральная задача (10), (11) с помощью дискретизации координаты φ по методу прямых сведена к канонической задаче (16), для решения которой применим использовавшийся метод ортогональной прогонки. В таблице 1 приводятся предельные значения фазовой скорости первой кромочной моды в зависимости от угла клина в вершине (в пересчете на толщину клина в основании h2) (колонка 1), найденные для материала с коэффициентом Пуассона υ = 0,25 по теории пластинок Кирхгофа-Лява (колонка 2), Тимошенко — (колонка 3), в рамках изложенной в этой статье методики расчета трехмерного клина (колонка 4–5) и по формуле ![]() [2], m = 1, 2, …, mφ < 90° (колонка 6). Колонка 4 соответствует варианту расчета с тремя внутренними прямыми (N = 3) и краевыми условиями (8), колонка 5 соответствует краевым условиям при том же количестве прямых:
[2], m = 1, 2, …, mφ < 90° (колонка 6). Колонка 4 соответствует варианту расчета с тремя внутренними прямыми (N = 3) и краевыми условиями (8), колонка 5 соответствует краевым условиям при том же количестве прямых:
![]()
В соответствии с численными и приведенными в таблице 1 результатами, варианты расчета по методам Кирхгофа-Лява, Тимошенко и трехмерной теории согласуются между собой в пределах 7% для углов клина с толщиной в основании h2, не превышающей 0,5 (угол клина φ0 = 28°).
Таблица 1
|
И2 |
|
K/A |
T |
3(1) |
3(2) |
A |
|
0,2 |
110 |
0,2 |
0,196 |
- |
- |
0,182 |
|
0,3 |
170 |
0,3 |
0,286 |
0,308 |
0,298 |
0,276 |
|
0,5 |
280 |
0,5 |
0,442 |
0,475 |
0,462 |
0,433 |
|
0,7 |
380 |
0,7 |
0,563 |
0,605 |
0,592 |
0,574 |
|
1 |
530 |
1 |
0,691 |
0,741 |
0,729 |
0,736 |
|
2 |
900 |
2 |
0,864 |
0,908 |
- |
0,92 |
Таким образом, в отличие от волноводов с прямоугольным сечением в клиновидных волноводах с достаточно малым углом клина при анализе дисперсионных зависимостей первой моды допустимо использовать теорию пластинок Кирхгофа-Лява. Установленный факт объясняется явлением локализации формы колебаний вблизи острого угла клина, описанный в [2]. Это явление следует рассматривать как характерную особенность динамического поведения пластинки переменной толщины.
Рис. 1. Расчетная схема
На основе полученных результатов сделаны следующие выводы:
— результаты расчета предельной скорости распространения первой моды в клиновидном волноводе по теории пластин Кирхгофа-Лява и по динамической теории упругости отличается не более, чем на 6% для углов вершины клина не превосходящих 28°. При ![]() результаты расчетов отличаются до 20%.
результаты расчетов отличаются до 20%.
Литература:
- И. И. Сафаров, З. Ф. Джумаев, З. И. Болтаев. Гармонические волны в бесконечном цилиндре с радиальной трещиной с учетом демпфирующей способности материала. Проблемы механики. 2011. с.20–25.
- И. И. Сафаров, М.Х.. Тешаев, З. И. Болтаев. Математическое моделирование волнового процесса в механическом волноводе с учетом внутреннего трения. Германия. LAP. 2013. 243с.







