В настоящее время происходит интенсивное развитие теории адаптивной обработки цифровых потоков данных [1, 2], на основе которой производится синтез высокоэффективных устройств цифровой обработки сигналов (ЦОС) в условиях воздействия коррелированных помех. Одна из основных целей таких устройств — подавить помеху. Следовательно, необходимо создать такой фильтр, который по заданному критерию наилучшим образом справляется с задачей уменьшения мощности мешающих компонент обрабатываемого цифрового потока. Проблема усложняется тем, что уровень мощности коррелированных помех может существенно меняться, по отношению к источнику аддитивного некоррелированного мешающего воздействия.
Одним из направлений теории и техники борьбы с коррелированными помехами является их обеление [1]. Рассмотрим широкий класс обеляющих фильтров (ОФ), преобразующих входную коррелированную помеху к белому шуму. При этом процесс на входе ОФ, после операции свертки с коэффициентами aw его импульсной характеристики (ИХ), преобразуется на выходе к процессу типа белого шума. При вычислении оптимального импульсного отклика фильтра необходимо выполнять обращение корреляционных матриц (КМ) помехового процесса. Вычислительная сложность процедуры обращения матриц достаточно велика, поэтому предназначенные для решения задач ЦОС в реальном масштабе времени алгоритмы обращения должны допускать распараллеливание, конвейеризацию или упрощения вычислений.
Оценка параметров адаптивного ОФ предполагает пересчёт коэффициентов обратной КМ мешающего процесса при изменении уровня мощности его шумовой составляющей. Известное упрощенное решение заключается в сохранении прежних значений вектора обработки, т. е. не предполагает адаптацию к изменяющейся мощности некоррелированной компоненты, что характерно, например, для режекторных фильтров [1]. Предлагаемое решение сохраняет алгоритм адаптации к изменяющейся мощности некоррелированной компоненты, но при этом процедура обращения матриц заменяется приблизительными расчетами, в результате чего резко сокращаются вычислительные затраты на синтез ОФ.
На практике принято разбивать задачу обработки сигналов на фоне аддитивных коррелированных помех и некоррелированных помех на два этапа [1]: 1) подавление коррелированных помех; 2) накопление полезного сигнала. Если его параметры неизвестны, то 2-й этап реализуется многоканальной структурой [1].
Статья посвящена решению 1-й задачи — построению адаптивного нерекурсивного фильтра подавления коррелированных помех, заданного q-го порядка. При этом предполагается, что частота Fs полезного сигнала априорно неизвестна и имеет равномерную функцию плотности распределения вероятностей по всему диапазону анализируемых относительных частот FsT![]() [0;1], где Т — интервал между наблюдениями. Упрощения, которые допускаются при синтезе ОФ, связаны с предположением о значительном превышении мощности Pc коррелированной компоненты над мощностью Pn некоррелированной составляющей. При этом эффективность системы обработки в целом, например, средняя вероятность
[0;1], где Т — интервал между наблюдениями. Упрощения, которые допускаются при синтезе ОФ, связаны с предположением о значительном превышении мощности Pc коррелированной компоненты над мощностью Pn некоррелированной составляющей. При этом эффективность системы обработки в целом, например, средняя вероятность ![]() правильного обнаружения полезного сигнала, оценивается путём усреднения величины D правильного обнаружения по неизвестному параметру FsT [1].
правильного обнаружения полезного сигнала, оценивается путём усреднения величины D правильного обнаружения по неизвестному параметру FsT [1].
Цель работы — сокращение вычислительных затрат при синтезе адаптивного обеляющего коррелированные помехи фильтра в условиях изменения мощности Pn некоррелированной компоненты мешающего аддитивного процесса.
Постановка задачи. Представим (q+1)×(q+1)‑мерную корреляционную матрицу R стационарного центрированного мешающего процесса как сумму коррелированной Rс и некоррелированной PnI компонент соответственно:
![]() ,(1)
,(1)
где Rc — (q+1)×(q+1)‑мерная корреляционная матрица коррелированной компоненты мешающего процесса, I —единичная матрица.
Нахождение параметров aw обеляющего фильтра сводится к виду [3]:
где ![]() — корреляционная матрица, аналогичная представленной в выражении (1) матрице R, мерность которой сокращена до (q×q); rT= [R1; R2; …; Rq] — автокорреляционная последовательность (дискретная автокорреляционная функция) мешающего процесса, T — знак транспонирования.
— корреляционная матрица, аналогичная представленной в выражении (1) матрице R, мерность которой сокращена до (q×q); rT= [R1; R2; …; Rq] — автокорреляционная последовательность (дискретная автокорреляционная функция) мешающего процесса, T — знак транспонирования.
Как видно из выражения (2), нахождение параметров aw подразумевает обращение корреляционной матрицы ![]() , являющейся частью исходной КМ мешающего процесса R (q+1)×(q+1)-го порядка, и умножение её на вектор автокорреляции мешающего процесса.
, являющейся частью исходной КМ мешающего процесса R (q+1)×(q+1)-го порядка, и умножение её на вектор автокорреляции мешающего процесса.
Отметим, что вычислительные затраты, которые требует процедура обращения матрицы ![]() , пропорциональны кубу величины q, а в случае использования быстрых процедур обращения — квадрату q [2]. Для сокращения вычислительных затрат на адаптацию обеляющего фильтра к изменяющейся мощности Pn некоррелированной мешающей компоненты и в условиях значительного превышении мощности Pc коррелированной компоненты над некоррелированной Pn, предлагается перейти к процедуре приблизительных расчетов. Рассматривая выражение (1) и применяя известное выражение для разности квадратов двучлена, запишем тривиальное равенство:
, пропорциональны кубу величины q, а в случае использования быстрых процедур обращения — квадрату q [2]. Для сокращения вычислительных затрат на адаптацию обеляющего фильтра к изменяющейся мощности Pn некоррелированной мешающей компоненты и в условиях значительного превышении мощности Pc коррелированной компоненты над некоррелированной Pn, предлагается перейти к процедуре приблизительных расчетов. Рассматривая выражение (1) и применяя известное выражение для разности квадратов двучлена, запишем тривиальное равенство:
![]() ,(3)
,(3)
Учитывая, что Pc >> Pn, пренебрегая вторым слагаемым левой части в выражении (3) Pn2I ≈ 0 возможно использовать, при процедуре обращения матрицы R, упрощения следующего характера [3]:
![]() ,(4)
,(4)
Вычислительные затраты при этом снижаются до величины ![]() арифмитических операций [3].
арифмитических операций [3].
Другой возможный способ приблизительных расчетов базируется на выражении для суммы кубов двучлена. Запишем тривиальное равенство:
![]() ,(5)
,(5)
Следовательно, можно использовать, при процедуре обращения матрицы R, упрощения следующего характера [3]:
Вычислительные затраты при этом снижаются до величины ![]() арифмитических операций [3].
арифмитических операций [3].
Оценка эффективности. Сравним вычислительные затраты на адаптацию при известном и предлагаемом решениях. В таблице приведены приближенные формулы для оценки вычислительных затрат.
Таблица 1
Вычислительные затраты
|
Известный метод |
Предлагаемый метод |
||
|
Квадратичное представление |
Кубичное представление |
||
|
Общее количество арифметических операций |
|||
|
(q+1)3 |
2(q+1) |
4(q+1) |
|
Из анализа таблицы следует, что при порядке фильтра q=3 выигрыш в вычислительных затратах составляет 8 раз при квадратичном представлении и 4 раза при кубичном представлении; при q=4–12,5 раз и 6,25 раз, а при q=5–18 раз и 9 раз соответственно.
На рисунке 1 изображены две нормированные к своему максимальному значению спектральные плотности мощности (СПМ) комбинированной помехи (пунктирная линия 1), квадраты амплитудно-частотных характеристик (АЧХ) предлагаемого квадратичного представления (сплошная жирная кривая 3), предлагаемого кубичного представления (кривая из жирных точек 4) и известного адаптивного (сплошная тонкая линия 2) фильтров при q=5 и двух значений относительной мощности некоррелированного шума: Pn=10−5 (рисунок 1а) и Pn=10−2 (рисунок 1б) во всём диапазоне относительных частот FT![]() [0…1 [, где F — доплеровская частота. Из рисунка 1 видно, что в зоне подавления коррелированной помехи (FT=0), при малых значениях Pn (диаграмма слева) наблюдается фактическое совпадение квадратов АЧХ предлагаемых и известного адаптивных фильтров, а при увеличении шумовой составляющей в 1000 раз (диаграмма справа) предлагаемые решения имеет зауженную зону прозрачности для полезного сигнала и излишне глубокую зону подавления помехи.
[0…1 [, где F — доплеровская частота. Из рисунка 1 видно, что в зоне подавления коррелированной помехи (FT=0), при малых значениях Pn (диаграмма слева) наблюдается фактическое совпадение квадратов АЧХ предлагаемых и известного адаптивных фильтров, а при увеличении шумовой составляющей в 1000 раз (диаграмма справа) предлагаемые решения имеет зауженную зону прозрачности для полезного сигнала и излишне глубокую зону подавления помехи.
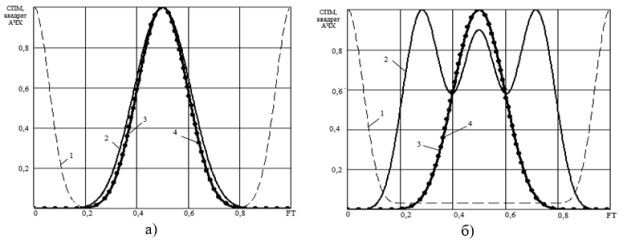
Рис. 1. Квадраты АЧХ-фильтров и СПМ-помехи при различной мощности некоррелированного шума
Отметим, что при малых мощностях (Pn→0) некоррелированной компоненты все решения дают одинаковый результат, поскольку обращение корреляционных матриц в известном и предлагаемых фильтрах сводятся к упрощенным выражениям (4), (6). При больших мощностях Pn≈Pc некоррелированной мешающей компоненты, достигающих уровня Pc коррелированных помех, предлагаемые адаптивные фильтры становится фактически заграждающим и использование адаптации по предлагаемым методикам теряет смысл. Поэтому адаптация целесообразна при уровнях мощности Pn некоррелированной компоненты, малом по сравнению с уровнем мощности Pc коррелированной помехи. При этом последнее условие наиболее часто встречается на практике [1].
Дадим численный анализ эффективности предлагаемой методики (3) обращения корреляционной матрицы адаптивного фильтра подавления корреляционных помех по критерию изменения мощности P на выходе ОФ. Нормированная величина P или коэффицент прохождения помехи определяется выражением [1]:
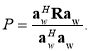 (7)
(7)
Для учёта прохождения полезного сигнала воспользуемся анализом коэффициента улучшения отношения сигнал‑(помеха+шум) по всем доплеровским частотам Fs. Коэффициент улучшения — это сумма значение коэффициента подавления помехи и коэффициента прохождения сигнала, представленных в дБ. Очевидно, что коэффициент подавления помехи величина обратная коэффиценту P прохождения помехи. При этом коэффициент подавления помехи, выраженный децибеллах, будет представлять собой противоположное значение –PdB коэффицента прохождения помехи, так же выраженного в дБ. Кэффициент Ps прохождения сигнала рассчитаем по следующему выражению:
![]()
(8)
где ![]() — квадрат амплитудного спектра на выходе обеляющего фильтра, L — число спектральных отсчётов. Коэффициент µdB улучшения отношения сигнал‑(помеха+шум) определяется соотношением:
— квадрат амплитудного спектра на выходе обеляющего фильтра, L — число спектральных отсчётов. Коэффициент µdB улучшения отношения сигнал‑(помеха+шум) определяется соотношением:
![]() (9)
(9)
Также при анализе эффективности ОФ воспользуется критерием Неймана — Пирсона, который предполагает максимизацию вероятности D правильного обнаружения при заданной вероятности F ложной тревоги, и сравним характеристики обнаружения для ОФ, реализующих известное решение обращения КМ, а также предлагаемое решение (3). Для этого оценим среднюю по относительным частотам FsT сигнала вероятность ![]() правильного обнаружения при вероятности ложной тревоги F=103, порядке фильтра q=5, уровне мощности шумовой мешающей компоненты Pn=10–2, относительной ширине спектра помехи ΔFT=0,1. Средняя вероятность
правильного обнаружения при вероятности ложной тревоги F=103, порядке фильтра q=5, уровне мощности шумовой мешающей компоненты Pn=10–2, относительной ширине спектра помехи ΔFT=0,1. Средняя вероятность ![]() правильного обнаружения определяется выражением:
правильного обнаружения определяется выражением:
![]() (10)
(10)
где Q — отношение сигнал‑(помеха+шум).
На рисунке 2 представлены зависимости средней вероятности ![]() правильного обнаружения от отношения Q сигнал-(помеха + шум) по мощности, представляющего собой отношение мощности полезного сигнала к сумме мощностей мешающих процессов на входе системы обработки. Из рисунка 2 видно, что предлагаемые решения (сплошная жирная кривая 2 и кривая из жирных точек 3) в среднем проигрывают в вероятности правильного обнаружения адаптивному известному (сплошная тонкая кривая 1) ОФ.
правильного обнаружения от отношения Q сигнал-(помеха + шум) по мощности, представляющего собой отношение мощности полезного сигнала к сумме мощностей мешающих процессов на входе системы обработки. Из рисунка 2 видно, что предлагаемые решения (сплошная жирная кривая 2 и кривая из жирных точек 3) в среднем проигрывают в вероятности правильного обнаружения адаптивному известному (сплошная тонкая кривая 1) ОФ.
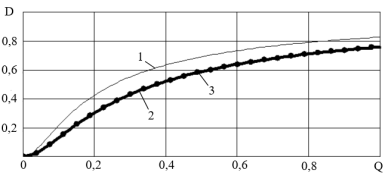
Рис. 2. Зависимости средней вероятности правильного обнаружения от отношения сигнал-(помеха+шум)
Выводы. Таким образом, произведён синтез адаптивных нерекурсивных фильтров, обеляющих комбинированные помехи, представляющие собой аддитивную смесь (1) коррелированной и быстро изменяющей свою мощность Pn некоррелированной мешающих компонент входного процесса. Предлагаемые алгоритмы адаптации целесообразно использовать при уровнях мощности Pn шумовой компоненты значительно меньшей мощности Pc коррелированной помехи. При этом с увеличением порядка q фильтра (q>3) предлагаемые решение значительно сокращает вычислительные затраты (для q=5 в 18 раз и 9 раз соответственно) на реализацию адаптации. Анализ эффективности предлагаемых решений показал, что они обладают выигрышем в вычислительных затратах пропорционально квадрату порядка q фильтра по отношению к известному решению (см. таблицу). При этом проигрыш в коэффициенте µdB улучшения сигнал‑(помеха+шум) составляет 1,6 Дб. Это приводит к тому, что предлагаемое решение уступает в средней вероятности ![]() правильного обнаружения потенциальной системе на 3…8 процентов.
правильного обнаружения потенциальной системе на 3…8 процентов.
Литература:
- Бакулев П. А. Радиолокационные системы.— М.: Радиотехника, 2004. 319 с.
- Марпл-мл. С. Л. Цифровой спектральный анализ и его приложения: пер. с англ. М.: Мир, 1990. 584 с.
- Андреев В. Г., Нгуен Т. Ф. Адаптивная обработка сигналов на фоне комбинированных помех // Изв. вузов. Радиоэлектроника.— 2015.— Т. 58.— № 2.— C. 48‑53.
- Нгуен Т. Ф., Андреев В. Г. Адаптивный быстродействующий алгоритм подавления комбинированных помех // Научный резерв: сборник статей триместрового военно-научного журнала. — № 14 — Рязань: 2014.— C. 60‑61.







