В статье описывается создание математической модели построения оптимального маршрута с учётом загруженности дорог.
Ключевые слова: ГИС, коэффициент загруженности дорог, оптимальный маршрут, построение оптимального маршрута.
Индустрия путешествий, по-другому туризм, процветает и занимает лидирующие позиции среди других отраслей экономики [1]. Но и у него имеются недостатки, особенно заметные для путешественника, стремящегося сэкономить [2]. Не у каждого автомобилиста, отправившегося в путь, есть собственный навигатор, который позволил бы не только не заблудиться, но и показать достопримечательности незнакомого города и построить оптимальные маршруты между объектами культуры, чтобы в кратчайшие сроки посетить интересующие места. Кроме того, навигаторы являются очень дорогостоящей вещью. Существует ряд программных продуктов, в разной степени показывающие основные достопримечательности и строящие оптимальные маршруты между ними. Большинство из таких систем платные, в бесплатных же программах не хватает той или иной функции.
Это наводит на мысль разработки своего программного средства, позволяющего быстро сориентироваться в незнакомом городе, вывести список интересных достопримечательностей, а также построить оптимальный маршрут для передвижения между ними. Это существенно упростит жизнь любого туриста, который рискнул отправиться в путешествие своим ходом — «дикарём».
Для разработки программного продукта такого плана потребовалась своя математическая модель построения оптимального маршрута между выбранными объектами.
Был проанализирован ряд алгоритмов построения оптимального пути, но ни один не учитывал ситуацию, которая может возникнуть на дороге [3].
Существует матрица расстояний U, записанная как (1):
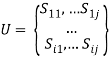; (1)
где: U — матрица расстояний,
(
и 
.) — расстояние между i и j пунктом. Заданы следующие условия:
a) i = j (например 
), то расстояние считается равным 0.
b) Расстояния и 
не обязательно совпадают.
c) Если между пунктами нет дороги, то считаем, что она есть, но принимаем её за бесконечность.
Для построения оптимального маршрута в городе, где пробки постоянны, использовать матрицу расстояний в километрах не всегда правильно, потому что ввиду загруженности дороги оптимальный путь между объектами может оказаться совершенно иной.
Тогда делаем преобразование из матрицы расстояний и построим матрицу времени A, которая будет выглядеть как 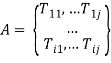(2):
; (2)
где: A — матрица времени,
( и .) — время пути между i и j пунктом. Заданы следующие условия:
a) Время между двумя пунктами рассчитаны благодаря расстояниям из матрицы U при езде со скоростью 60 км/ч, если отсутствуют пробки на дороге.
b) i = j (например
), то время считается равным 0.
c) Время
и 
не обязательно совпадают.
d) Если между пунктами нет дороги, то время пути принимается за бесконечность.
Для верного алгоритма подсчёта оптимального времени в зависимости от времени суток и дня недели, был сделан недельный мониторинг Яндекс карт города Уфы [4]. Он показал, что наибольшая загруженность дорог:
- В будние дни 8:00–10:00 и 18:00–19:00 для центральных улиц города.
- В будние дни 8:00–10:00 и выходные/праздничные дни 18:00–23:00 для нецентральных улиц города.
На основе собранных данных был составлен коэффициент загруженности дороги, который выглядит как:
В остальных случаях для центральных улиц:
a) z = 1, в будние дни 11:00–17:00, 20:00–7:00, в выходные/праздничные дни: 23:00–12:00.
b) z = 2, в выходные/праздничные дни: 12:00–18:00.
c) z = 3, в выходные/праздничные дни: 18:00–23:00.
d) z = 4, в будние дни 7:00–8:00, 10:00–11:00, 17:00–18:00, 19:00–20:00.
e) z = 5, в будние дни 8:00–10:00 и 18:00–19:00.
Для нецентральных улиц:
a) z = 1, в будние дни 10:00–17:00, 20:00–8:00, в выходные/праздничные дни: 23:00–11:00.
b) z = 2, в выходные/праздничные дни: 11:00–18:00.
c) z = 3, в будние дни 8:00–10:00 и выходные/праздничные дни 18:00–23:00.
Таким образом окончательная матрица времени будет выглядеть 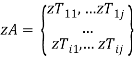(3):
; (3)
Получаем итоговую математическую модель (4):
(4)
где T — общие временные затраты на маршрут между достопримечательностями, состоящие из суммы времени пути между пунктами умноженные коэффициент на загруженности дороги, последовательно включённых в маршрут.
Литература:
- Биржаков М. Б. Введение в туризм. Учебное пособие СПб., 2000. 192 с.
- Квартальнов В. А. Туризм. Учебник. М., 2002. 320 с.
- Сетевые методы решения задачи коммивояжёра / Успехи современного естествознания URL: https://www.natural-sciences.ru/ru/article/view?id=30093 (дата обращения: 27.04.2018).
- Яндекс карты Уфа / Яндекс карты URL: https://yandex.ru/maps (дата обращения: 07.05.2018).
