В статье исследуются вопросы, связанные с обслуживанием неординарного потока заявок одним прибором. Целью исследования, проведенного в статье, является нахождение условий, при которых существуют предельные распределения величин числа требований в очереди (длина очереди), а также длительности ожидания начала обслуживания группы требований.
Ключевые слова: поток требований, системы массового обслуживания, неординарный поток требований, теорема Линдии — Финча
1. Постановка задачи
Неординарный поток требований обслуживается одним прибором. Относительно входящего потока и обслуживающей системы мы сделаем следующие предположения:
1) Поток требований по обслуживанию является неординарным потоком типа 
, из этого следует, что:
• Моменты поступления требований 
таковы, что разности 
при 
образуют последовательность независимых случайных величин, имеющих одна и ту же функцию распределения:
(1)
• Число требований, поступивших в вызывающий момент 
, является случайной величиной 
, для которой:
(2)
2) Длительность обслуживания на приборе различных требований — независимые случайные величины 
с распределением:
(3)
3) Если требования поступают в момент, когда прибор свободен, то обслуживание начинается через случайное время 
, распределенное по закону:
(4)
4) Требования, заставшие прибор занятым, становятся в очередь вслед за всеми ранее прибывшими требованиями. Требования одной группы обслуживаются по одному в произвольном порядке;
5) Величины 
независимы при всех i, j, n, причем:
6) Прибор, начавший обслуживание, доводит его до конца и после окончания обслуживания способен приступить к обслуживанию очередного требования, если оно имеется. Если в очереди на обслуживание имеются требования, то между концом обслуживания одного требования и началом обслуживания следующего нет никакого свободного промежутка времени.
Обозначим через 
— число требований в очереди (длину очереди) в момент 
, где момент выхода из обслуживавшей системы r-го обслуженного требования, а через 
- длительность ожидания начала обслуживания группы требований, прибывших в систему в вызывающий момент 
.
Ставится следующая задача: найти при каких условиях существуют предельные распределения величин и при 
.
2. Предельная теорема
В этом параграфе решается задача, поставленная в параграфе 1. А именно, имеет место следующая теорема:
Если 
, то существуют предельные распределения
(5)
(6)
Функция 
не зависит от распределения 
и является единственным решением интегрального уравнения
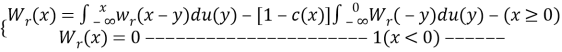(7)
где
(8)
(9)
Доказательство. Прежде чем привести доказательство теоремы, поясним наглядный смысл условия . Обозначим через 
— длительность обслуживания группы требований, прибывших в систему в вызывающий момент 
.
По формуле полной вероятности:
(10)
Но т. к.
(11)
и
(12)
то
(13)
Следовательно, функция 
определяемая формулой (9) является распределением величины 
В дальнейшем характеристическую функцию неотрицательной случайной величины 
с распределением 
будем обозначать через 
, т. е. 
Из (5) с учетом 
, 
вытекает
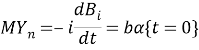(14)
Итак, с наглядной точки зрения условие 
означает, что среднее время обслуживания группы одновременно поступающих требований меньше, чем среднее время между последовательными вызывающими моментами. Теперь докажем теорему. Легко проверить, что величины и 
связаны между собой соотношениями
(15)
Применение теоремы Линдии — Финча [2] к последовательностям
и 
доказывает теорему. Существование предельного распределения следует из существования предельного распределения .
Литература:
- В. Сенатов, Центральная предельная теорема. Точность аппроксимации и асимптотические разложения, 2017 г. 47–52с
- А. Н. Колмогоров. Selected Works, Математический сборник, 1993 г., 168–172с
