Под методом обучения математике в среднем специальном учебном заведении будем понимать «способ развития деятельностей преподавателя, студента и математического содержания в ссузе» [1, с. 154]. Процесс обучения математике в среднем специальном учебном заведении с использованием новых информационных технологий (НИТ) представляет взаимодействие преподавания, учения и математического содержания в компьютерной среде обучения. Математическое содержание, представляет собой реализацию дидактических задач с использованием НИТ (актуализация знаний и умений с использованием электронного компьютерного практикума, дистанционных технологий, формирование математического понятия с использованием гипер- , медиа- технологий и т.д.). Дидактические задачи можно представить математическими задачами, допускающими их решение с использованием НИТ, а также профессионально значимых задач. Деятельность студента – познавательная деятельность, реализованная в компьютерной обучающей среде.
Использование НИТ позволяет разнообразить дидактические приемы преподавателя математики: поддержать интерес к изучению математики, активизировать познавательную деятельность студентов, эффективно организовать входной, текущий и итоговый контроль.
В условиях использования НИТ и учитывая особенности обучения математике в среднем специальном учебном заведении, целесообразно и эффективно использовать логико-алгоритмический метод или метод алгоритмизации.
Данный метод понимается в двух смыслах [2, с. 108]:
а) обучение студентов алгоритмам;
б) построение и использование алгоритмов самого обучения.
1. Под алгоритмом, как известно, понимается общепринятое и однозначное предписание, определяющее процесс последовательного преобразования исходных данных в искомый результат. Точное выполнение алгоритма всегда приводит к решению любой задачи из того класса задач, для которого он составлен. В математике существуют алгоритмы для решения задач разных классов, поэтому обучение математике на любом уровне обязательно включает обучение алгоритмам. Умение формулировать и применять алгоритмы важно не только для развития математического мышления и математических умений. Исследования показали, что студенты ссузов «быстрее и прочнее усваивают действия, имеющие отраженный в учебнике четкий алгоритм выполнения, преподносимый в форме показа операций. А для обучения решению технических задач наиболее эффективен способ обучения алгоритмам решения».
Существует два способа обучения алгоритмам:
а) сообщение готовых алгоритмов.
Значительно увеличивает объем усваиваемой информации студентами, однако ограничивает развитие их активности и творческого мышления. В этом случае использование средств НИТ позволяет демонстрировать весь алгоритм или по частям. Создавать целую базу алгоритмов решения задач определенного класса в электронном виде, к которой студенты могут обратиться в любой момент. А также выступать средством контроля усвоения последовательности операций в алгоритме. Средства НИТ позволяют студентам выполнять задания по математике с использованием динамических моделей, осуществлять численные и символьные вычисления.
Очень большим потенциалом для использования алгоритмического метода при обучении стереометрии студентов ссузов обладает электронный учебно-методический комплекс «Живая математика». Благодаря возможностям данной программной среды преподаватель может использовать уже готовые алгоритмы решения задач или доказательства теорем, а также создавать свои собственные. Возможности программы позволяют преподнести алгоритм студенту, используя интерактивные шаги и динамические рисунки. К каждому шагу можно вернуться заново и еще раз изучить его. Подобные алгоритмы очень эффективно использовать как при объяснении нового материала, так и для индивидуальной работы студента. На рисунке 1 приведен фрагмент использования алгоритмического метода при изучении темы «Двугранный угол». Процесс построения линейного угла двугранного угла представлен по шагам, которые предъявляются студентам постепенно в процессе объяснения. К любому шагу алгоритма можно вернуться еще раз. В любой момент можно также скрыть любой шаг алгоритма и проверить, как его усвоили студенты.

Рис. 1. Интерактивный алгоритм
б) подведение учащихся к самостоятельному открытию необходимых алгоритмов, что является вариантом эвристического метода обучения и предполагает реализацию все тех же трех этапов изучения математического материала - выявление отдельных шагов алгоритма, его формулировку и применение.
На первом этапе средства НИТ должны выступать как инструментарий преподавателя: при подведении учащихся к открытию определенных фактов и закономерностей, для демонстрации отдельных шагов алгоритма. На втором этапе средства НИТ используются для запоминания последовательности шагов и формулировки алгоритма. На этапе применения алгоритма происходит использование программных средств по математике для реализации решения задачи. Использование, например математических пакетов при изучении алгоритмов решения типовых задач, способствует возбуждению у студентов ссузов познавательного интереса, повышение работоспособности.
Например, рассмотрим ряд алгоритмов по теме «Производная и ее приложения» (таблица).
Таблица
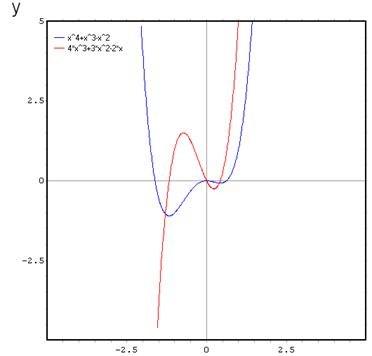
А л г о р и т м. Нахождение промежутков возрастания и убывания функции.
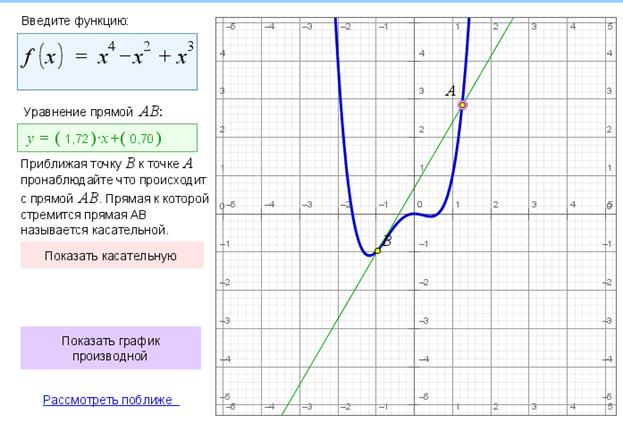
Рис. 2. Интерактивная модель «Геометрический смысл производной»
Кроме приведенных примеров по теме «Производная и ее приложения» можно составить алгоритмы нахождения:
–.производной функции по ее определению;
– точек перегиба функции;
– наибольшего и наименьшего значений функций на промежутке и др.
II. Второй аспект логико-алгоритмического метода состоит в построении алгоритмов обучения с использованием НИТ, т.е. в описании обучающей деятельности учителя с помощью предписаний, алгоритмического типа. Реальный процесс обучения состоит из определенных действий, с помощью которых, преподаватель традиционно решает определенные дидактические задачи. Например, постановка вопросов, приведение примеров, показ наглядного материала, решение упражнений и т. д. Этот процесс можно проанализировать и выявить составляющие его действия; тогда определённая часть процесса обучения определённых учащихся определенному содержанию может быть представлена в виде так называемого "алгоритма обучения" (в нашем курсе - "методическая схема").
Для построения алгоритма нужно проанализировать содержание и цели обучения, деятельность учащихся по его усвоению, деятельность учителя по организации этого усвоения с использованием компьютерной среды обучения. Построенный алгоритм обучения должен быть осуществим не только теоретически, но и практически, учитывать особенности студентов данной группы. Примерами алгоритмов обучения математике могут служить: обучение доказательству теорем, обучение решению задач и другие.
Литература:
1. Саранцев, Г.И. Методика обучения математике в средней школе: учеб. пособ. для пед. инстит. / Г.И. Саранцев, – М.: Просвещение, 2002. – 224 с.
2. Темербекова, А. А. Методика преподавания математике : учеб. пособ. для студентов высш. учеб. завед. / А. А. Темербекова. – М.: ВЛАДОС, 2003. 176 с.







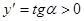
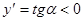

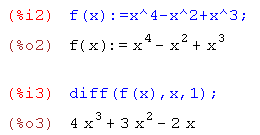
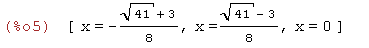
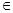 (-∞;-
(-∞;-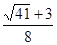 )
)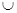 (0;
(0; 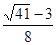 ).
).