Современные информационные системы требуют особого подхода к передаче электронных документов по открытым каналам связи, что обеспечивается с использованием систем безопасности.
Эффективная система безопасности информации должна обеспечивать:
§ секретность информации или наиболее важной ее части;
§ аутентичность субъектов и объектов информационного взаимодействия;
§ защиту от несанкционированного доступа;
§ защиту прав собственников информации;
§ оперативный контроль процессов управления, обработки и передачи информации.
Все перечисленные пункты, которым должна удовлетворять эффективная система безопасности информации, решаются с использованием генератора псевдослучайных последовательностей. Такие генераторы являются детерминированными алгоритмами и применяют в качестве входных данных начальное значение, а на выходе порождают последовательность значений, которая очень похожи на случайную. Определенность алгоритма является причиной приставки «псевдо» – выработанная последовательность подчиняется соответствующей алгоритму закономерности, то есть не является случайной.
По Мизесу последовательность бывает случайной и неслучайной [1]
Теорема 1. (Необходимый признак для последовательности из нулей и единиц) Если последовательность 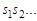 случайна, то существует средняя частота единиц, т.е. предел
случайна, то существует средняя частота единиц, т.е. предел 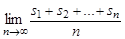 .
.
Предложенное необходимое условие Р. Мизесом было уточнено в дальнейшем А. Вальдом [2], А. Чёрчем [3].
Определение 1. Последовательность 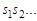 называется случайной по Мизесу-Чёрчу если выполняются два условия:
называется случайной по Мизесу-Чёрчу если выполняются два условия:
1. Существует предел 
2. Для любого разрешимого множество 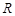 конечных последовательностей нулей и единиц либо подпоследовательность
конечных последовательностей нулей и единиц либо подпоследовательность 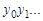 , полученная из исходной выбором тех членов
, полученная из исходной выбором тех членов 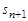 , для которых
, для которых 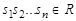 , конечна, либо предел
, конечна, либо предел 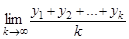 существует и равен
существует и равен 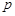
В дальнейшем вопрос о случайных последовательностях исследовался А.Н. Колмогоровым в работе [4] предложил на базе определения Мизеса-Чёрча усовершенствованное определение случайной последовательности. Для ввода этого определения потребуется правило выбора в терминах переворачивания карточек.
Правило выбора. Задается две вычислимые функции 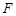 и
и 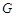 .
.
Функция 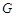 определяет, в каком порядке мы будем переворачивать карточки. Её аргументами является конечные последовательности нулей и единиц, а значениями – натуральные числа.
определяет, в каком порядке мы будем переворачивать карточки. Её аргументами является конечные последовательности нулей и единиц, а значениями – натуральные числа.
1. Переворачиваем карточку с номером 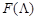 , где
, где 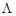 ‑ пустая последовательность. Обозначим написанное на ней число
‑ пустая последовательность. Обозначим написанное на ней число  или
или 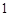 через
через 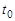 .
.
2. Переворачиваем карточку с номером 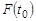 , обозначаем написанное на ней число
, обозначаем написанное на ней число 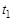 .
.
3. Переворачивается карточка с номером 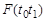 , написанное на ней число обозначается
, написанное на ней число обозначается 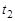 .
.
4. Переворачивается карточка с номером 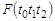 и т.д.
и т.д.
Функция 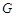 имеет аргументами конечную последовательность нулей и единиц, а значениями
имеет аргументами конечную последовательность нулей и единиц, а значениями  и
и 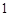 . Она определяет будет ли определен член в подпоследовательность или нет. Член с номером
. Она определяет будет ли определен член в подпоследовательность или нет. Член с номером 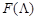 будет включен в подпоследовательность, если и только если
будет включен в подпоследовательность, если и только если 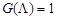 , член с номером
, член с номером 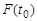 будет включен в последовательность, если и только если
будет включен в последовательность, если и только если 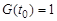 , член с номером
, член с номером 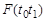 ‑ если и только если
‑ если и только если 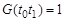 и т.д.
и т.д.
Порядок членов в последовательности определяется порядком их выбора с помощью функции 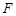 . Если в некоторый момент описанного процесса значения функции
. Если в некоторый момент описанного процесса значения функции 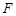 или
или 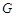 оказывается неопределенными, то процесс выбора обрывается и подпоследовательность оказывается конечной. То же самое происходит, если очередное значение функции
оказывается неопределенными, то процесс выбора обрывается и подпоследовательность оказывается конечной. То же самое происходит, если очередное значение функции 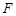 совпадает с одним из предыдущих.
совпадает с одним из предыдущих.
Приведем определение случайной последовательности, которое было сформулировано А.Н. Колмогоровым.
Определение 2. Последовательность 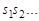 называется случайным по Мизесу-Колмогорову-Ловеланду если выполняется следующие два условия:
называется случайным по Мизесу-Колмогорову-Ловеланду если выполняется следующие два условия:
1. Существует предел 
2. Существует предел равный 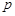 , для любой бесконечной последовательности полученной из
, для любой бесконечной последовательности полученной из 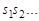 с помощью допустимого правила выбора.
с помощью допустимого правила выбора.
Определение случайной последовательности Мизесу-Колмогорову-Ловеланду называется так потому, что Ловеланд предложил аналогичное определение позже в своих работах.
В работе [3, 5] показано, что если последовательно случайна по Мизесу-Колмогорову-Ловеланду, то она случайна и по Мизесу-Чёрчу обратное не верно.
Позднее А.Н. Колмогоровым и его последователями были развиты другие, отличные от мизесовского, подходы к определению понятия случайной последовательности [6]. Подход в [6] называется теоретикомерный, аналогичный ему ‑ сложностный. Эти подходы приводят к одному и тому же классу случайных последовательностей; этот класс назваться классом случайных по Мартин – Лёфу названного в честь Мартина – Лёфа, который в 1965 г. в работе [6] дал одно из определений этого класса случайности. В след за Мартин -Лёфом дал определение в 1969 г. [7] Г. Чайтин используя сложностный подход.
Вычислительные последовательности оказываются не случайными по любому из выше приведенных определений. Мы будем опираться на идею А.Н. Колмогорова, которая состоит в том, чтобы «не случайными» считать последовательности, которых наблюдается достаточно много закономерностей, где под закономерностью подразумевается любое проверяемое свойство последовательности присущее лишь узкому их классу.
Проверку на принадлежность одному из классов последовательностей будем проводить с использованием тестов. Тесты, использующиеся для исследования псевдослучайных последовательностей, делят на две группы:
1. Графические тесты. Статистические свойства последовательности отображаются в виде графических зависимостей, по виду которых делаю выводы о свойствах исследуемой последовательности.
2. Оценочные тесты. Статистические свойства последовательности определяются числовым характеристиками. На основе оценочных критериев делаются заключения о степени близости свойств анализируемой и истинно случайной последовательностей.
Рассмотрим графический тест «Гистограмма распределения элементов». Этот тест позволяет оценить равномерное распределение символов в исследуемой последовательности, а также определить частоту появления каждого символа. Строиться гистограмма следующим образом. В исследуемой последовательности 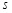 подсчитывается, сколько раз встречается каждый элемент, после чего строиться зависимость числа появлений элементов от их численного представления ASCII-значения для байтов.
подсчитывается, сколько раз встречается каждый элемент, после чего строиться зависимость числа появлений элементов от их численного представления ASCII-значения для байтов.
Алгоритм 1. Гистограмма распределения элементов
Вход. 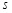 -последовательность байт.
-последовательность байт.
Выход. Возвращает гистограмму и значение истина-тест пройден, и ложь-тест не пройден.
1. Для 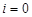 до
до 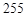 выполнять:
выполнять: 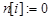
2. Для 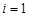 до
до 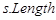 выполнять:
выполнять: 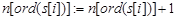
3. 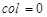
4. Для 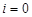 до
до 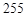 выполнять:
выполнять:
5. Если ( ) тогда
) тогда 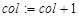
6. 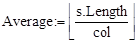
7. 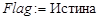
8. Для 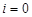 до
до 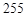 выполнять:
выполнять:
9. Если ( ) и ((
) и ((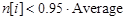 )или(
)или(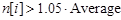 )) то
)) то 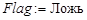
10. Вывод 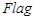 и
и 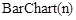
Рассмотрим следующий графический тест «Распределение на плоскости»
Данный тест предназначен для определения зависимостей между элементами исследуемой последовательности.
Построение распределения на плоскости осуществляется следующим образом. На поле размером 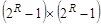 , где
, где 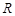 -разрядность чисел исследуемой последовательности, наноситься точки с координатами
-разрядность чисел исследуемой последовательности, наноситься точки с координатами 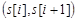 , где
, где 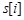 -элементы исследуемой последовательности
-элементы исследуемой последовательности 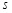 ,
, 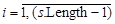 .
.
Если между элементами последовательности отсутствуют зависимости, то точки на плоскости располагаются хаотически, значит данная последовательность этот тест прошла, иначе нет. Для последовательности большой длины хорошим результатом является абсолютно черное поле.
Рассмотрим определение 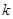 -распределенной последовательности данное Д. Кнутом в работе [8].
-распределенной последовательности данное Д. Кнутом в работе [8].
Определение 3 [8]. 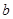 -ичная последовательность называется
-ичная последовательность называется 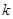 -распределенной, если
-распределенной, если 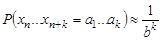 для всех
для всех 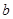 -ичных чисел
-ичных чисел 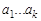 , где
, где 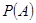 -вероятность события
-вероятность события 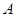 .
.
На базе понятия 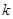 -распределенности в работе [8] вводится определение псевдослучайной последовательности.
-распределенности в работе [8] вводится определение псевдослучайной последовательности.
Определение 4. [8]. 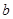 -ичная последовательность длины
-ичная последовательность длины 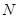 псевдослучайна, если она
псевдослучайна, если она 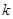 -распределена для всех положительных целых
-распределена для всех положительных целых 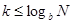
Одним из ярких представителей оценочных тестов является тест «Проверкай несцепленных серий» которая позволяет оценить равномерность распределения символов в исследуемой последовательности на основе анализа частоты появления нулей и единиц и серий, состоявших из 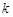 бит.
бит.
Построение осуществляется следующим образом. Подсчитывается, сколько раз встречаются нули, единицы, серии-двойки (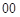 ,
, 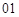 ,
, 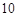 ,
, 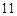 ), серии ‑ тройки (
), серии ‑ тройки (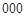 ,
, 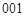 ,
, 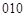 ,
, 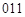 ,
, 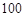 ,
,  ,
,  ,
, 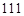 ) и т.д. в битовом представлении исследуемой последовательности
) и т.д. в битовом представлении исследуемой последовательности 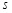 . Полученный результат представляется в графическом виде.
. Полученный результат представляется в графическом виде.
Алгоритм 2. Тест «Проверка несцепленных серий»
Вход. 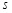 -последовательность бит
-последовательность бит
Выход. Возвращает истина, если тест пройден, иначе ‑ ложь
1. 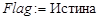
2. Для 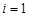 до
до 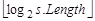 выполнять:
выполнять:
2.1. Для 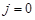 до
до 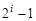 выполнять:
выполнять: 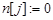
2.2. 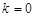
2.3. Пока 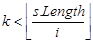 выполнять:
выполнять:
2.3.1. 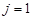
2.3.2. 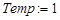
2.3.3. 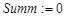
2.3.4. Пока 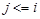 выполнять:
выполнять:
2.3.4.1. 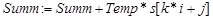
2.3.4.2. 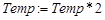
2.3.4.3. 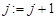
2.3.5. 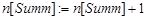
2.3.6. 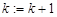
2.4. 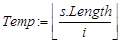
2.5. Для 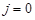 до
до 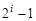 выполнять:
выполнять:
2.5.1. Если (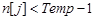 ) или (
) или (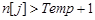 ) то
) то 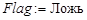
3. Вывод 
Данный критерий можно усовершенствовать, используя критерий 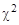 . Пусть результат испытаний таковы, что их можно разделить на
. Пусть результат испытаний таковы, что их можно разделить на 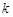 категорий. Проводится
категорий. Проводится 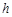 независимых испытаний, где
независимых испытаний, где 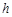 - достаточно большое число. Пусть
- достаточно большое число. Пусть 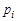 ‑ вероятность того, что результат испытаний попадает в
‑ вероятность того, что результат испытаний попадает в 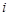 категорию, а
категорию, а 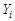 - число испытания, которые попали в
- число испытания, которые попали в 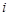 -ю категорию при проведении испытаний. Тогда
-ю категорию при проведении испытаний. Тогда 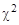 вычисляется по формуле:
вычисляется по формуле:
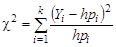
Для оценки полученных результатов используют таблицу 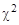 .
.
Применяя критерий 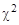 к проверки несцепленных серий, получим:
к проверки несцепленных серий, получим:
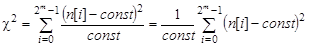 , где
, где 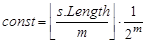
Полученный результат анализируется при помощи критерия 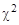 с числом степеней свободы равным
с числом степеней свободы равным 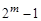
Покажем применение двух алгоритмов к псевдослучайной, последовательности полученной при использование пакета PARI/GP. Для программирования воспользуемся средой разработки FreePascal.
Результат прохождения графического теста при 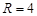 и
и 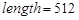 .
.

Рисунок 1. Распределения на плоскости для последовательности полученной с помощью PARI/GP.
Из рисунка 1 следует, что последовательность, генерируемая PARI/GP, не является псевдослучайной, так как имеет решетчатую структуру..
Тест на несцеплинные серии данный генератор тоже не прошел.
В статье показано, что генератор псевдослучайных чисел, построенный с использованием программы PARI/GP, является статистически не безопасным, и поэтому его лучше не применять на практике для построения псевдослучайных последовательностей.
Литература:
1. Мизес Р., Вероятность и статистика, М.-Л., 1930, 16 с.
2. Wаld A., Die Wiederschpruchsfreiheit des Kollektivbegriffs der Wahrscheinlichkeitsrechnung, Ergebnisse eines mathemathishen Kolloquiums 8, 1937, P. 38-72.
3. Church A., On the concept of random sequence, Bull. Amer. Math. Soc. 46, 1940, P. 254-260.
4. Kolmogoroff A., On the tables of random numbers, Sankhya Indian Jorn. Statist., ser. A 25 1963, P. 369-376.
5. Звонкин А.К., Левин Л.А., Сложность конечных объектов и обоснование понятий информации и случайности с помощью теории алгоритмов, Успехи математических наук, 25:6(156), 1970, С. 85-127
6. Per Martin-Lof. The Definition of Random Sequences. //Information and Control, 9(6): 1966, P. 602-619.
7. Chaitin G.J. On the length of programs for computing finite binary sequences: statistical considerations.// Journal of the ACM 16 (1969), P. 145-159.
8. Кнут Д. Искусство программирования. – Т. 2. Получисленные алгоритмы, 3-е изд. – М.: Издательский дом «Вильямс», 2000 – 832 с.







