The application of a definite integral to solving the problem of the economy

In this article we consider the importance of a definite integral in the construction of economic problems for research and modeling processes in the economy.

Keywords: integral calculus, definite integral, forecasting of economic processes, mathematical analysis.

Elements of mathematical analysis occupy a significant place in the field of mathematics. The language of the derivative and integral allows us to formulate many laws of nature. In the course of mathematics with the help of differential and integral calculus, the properties of functions are investigated, their graphs are constructed, the problems for the largest and smallest values are solved, the lengths, areas and volumes of geometric figures are calculated. However, the possibilities of mathematical analysis methods by such problems are not exhausted. In physics, the integral is used to calculate the work of the variable force, the path traveled by the body, finding the fluid pressure on the vertical plate, calculating the static moments and the coordinates of the center of gravity of the plane curve; biology of populations, average length of flight of birds. The above examples do not exhaust the possible applications of a definite integral. We can also give a lot of examples of the application of a definite integral. We were interested in the use of a certain integral for solving various economic problems. The integral appeared as a response to the need to find volumes and areas.

For the first time such calculi were asked by mathematicians of ancient Greece. In our time, the integral is applied in various spheres, in the work the authors examined the application of a definite integral for solving economic problems on finding the productivity of labor, the volume of output and depreciation charges.

Integration is the opposite of differentiation. I. Barrow first saw the connection between integration and differentiation. Later, Newton and Leibniz, independently of each other, derived a formula that we know as Newton-Leibniz:

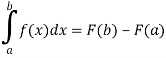
This event marked the emergence of a general method of integral and differential calculus. The Russian scientist P. L. Chebyshev proved that there exist integrals which can not be expressed in terms of elementary functions. A rigorous presentation of the theory of integrals was due to the work of O. Cauchy.

The symbol of the integral — ∫ was introduced by Leibniz in 1675. It is a modified Latin letter S, which is the first letter in the word sum. Termin integral was invented by J. Bernoulli in 1690. Most likely, it comes from the Latin word «integero», which in translation means «to restore, restore», because the integration operation as if «restores» the function, from which the integrand was obtained by differentiation.

The integral is the result of the addition of an infinite large number of infinitely small summands, in other words, we mean the partition of the domain of integration that is a segment into a set of infinitesimal segments, and also the sum of the products of the value of the argument function that belongs to each segment, and the length of the corresponding infinitesimal segment of the integration domain, in the limit, infinitely small partition:

An indefinite integral of f(x) is the collection of all antiderivatives for a function f (x) on the interval X

The definite integral, in the geometric sense, is numerically equal to the area of ​​the figure, which is bounded by the abscissa axis, the lines x = a and x = b and the graph of the function f (x), formula definite integral:

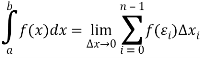
In the modeling of economic processes, the role of the integral is not considered so often, but, despite this integral calculus, a rich mathematical apparatus provides the modeling and research of the processes taking place in the economy. The calculation of the areas of different figures, the determination of the volumes of geometric bodies, and certain applications in physics and technology are illustrated by an application of the integral.

Let us dwell on some examples of the use of integral calculus in the economy. To begin with, consider the concept of consumer surplus in a market economy. And therefore we will consider some economic concepts and notation. Application of a definite integral in modeling and solving economic problems.

Average time of product manufacturing

Let the function t=t(x) be known, describing the change in the time spent t on the manufacture of the product, depending on the degree of production mastering, where x is the serial number of the product of the batch. Then the average time t_av spent on making one product in the period from to products is calculated by the mean value theorem:

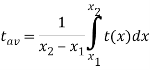(1)

The function of changing the time spent on manufacturing products t=t(x) often has the form: t=, where a is the time spent on the first product, and b is the production process indicator.

Solution: Using formula (1), we obtain

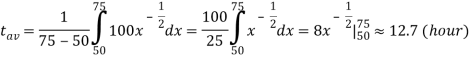
When using the integral method, the condition of continuous differentiability of the function must be observed, where as an argument any economic coefficient is taken. Regardless of the number of components that are included in the model, and in addition, regardless of the form of communication between these components, integral calculus determines the cumulative approach to solving models of different types. With its use, there is a way to obtain more reasoned results of calculating the effects of individual factors, rather than using other methods. It is difficult to name a scientific field in which mathematical methods of studying real objects and processes were not applied. One of the most important branches of mathematics used to describe and solve applied problems is integral calculus. The examples of practical problems considered in this paper give us a clear idea of the significance of a definite integral. So in the process of implementation, examples of practical problems in the field of economics solved using a definite integral were considered. Of course, this is far from an exhaustive list of problems that use the integral method, but even they show a wide application of this method in solving real applied problems. Of course, the economy is by no means the only sphere of application of integrals, but the solution of economic problems with the help of a definite integral helped us to realize importance of the method of integral calculus. The examples given are only emphasize the need to use a mathematical tool to solve problems with economic content.

References:

1. Mathematical analysis. T. Azlarov., X. Mansurov. Tashkent “Teacher” — 1994.
2. S. M. Krass, P. B. Chuprinov. The foundations of mathematics and its application in economic education. 2003.
3. M. R. Nureev. Microeconomics course: textbook for high schools. -М.: Norm, 2005.