Приводятся интервальные алгоритмы настройки адаптивных регуляторов с неопределенными параметрами. Освящена разработка адаптивно-интервальных алгоритмов синтеза систем управления технологическими объектами. Рассмотрена возможность применения апериодическую регулятора при интервальной неопределенности параметров для адаптивных систем управления с неявной эталонной моделью.
Ключевые слова: интервальный анализ, идентификация, регулятор, адаптивно-интервальная система управления, вектор управления.
Главной современной проблемой развития науки, техники и технологии являются фундаментальные исследования в области моделирования, управления, качественного и количественного анализа динамики сложных систем. Необходимость разработки новых качественных и количественных методов исследования динамики систем, построения программных управлений связана с поиском условий устойчивого, надежного и безопасного функционирования сложных динамических систем, имеющих различные особенности.
Интервальный анализ и его специфичные методы имеют, таким образом, наивысшую ценность в задачах, где неопределённости и неоднозначности возникают с самого начала и являются неотъемлемой частью постановки задачи. Хотя это никоим образом не исключает других плодотворных применений интервального анализа, в частности, в задачах, формулируемых вообще без привлечения понятия интервала. Например, в последние десятилетия интервальный анализ получил широчайшее распространение в качестве основы для так называемых доказательных (достоверных, надёжных) вычислений на ЭВМ, вычислений с гарантированной точностью и т. п., несмотря на то, что в этих приложениях интервальные методы являются всего лишь вспомогательным средством для решения задач, неинтервальных по своей природе.
Интервальное представление неопределённости стало привлекать всё большее внимание математиков и практиков потому, что оно является наименее ограничительным и отвечает широкому классу прикладных задач, в которых часто нет оснований или недостаточно информации для того, чтобы рассматривать эту неопределённость как случайную, т. е. подчиняющуюся теоретико-вероятностным моделям. Интервальный анализ и возникшая практически одновременно с ним теория нечётких множеств явились ответом на вызов бурно развивающейся практики, которая требовала развития аппарата для учёта неопределённостей нестатистической (или, в общем случае, неизвестной) природы. При этом интервальный анализ оказался способным исследовать содержательные модели, которые основываются на наиболее скудных априорных допущениях о характере неопределённости, когда относительно рассматриваемых величин ничего не известно, кроме их свойства принимать значения из некоторых ограниченных множеств [1].
Во многих работах, касающихся синтеза алгоритмов идентификации объекта и настройки управляющего устройства, является предположение о том, что оценки параметров объекта совпадают с их истинными значениями. С практической точки зрения такое предположение является чрезмерно ограничительным. Вместе с тем для многих практических ситуаций вполне достаточным оказывается предположение о принадлежности оценок некоторым фиксированным числовым интервалам, что делает вполне оправданным подход к решению задачи синтеза алгоритмов настройки регулятора с помощью аппарата интервального анализа [2–3].
Данная работа посвящена разработке адаптивно-интервальных алгоритмов синтеза систем управления технологическими объектами. Сформулируем постановку задачи синтеза адаптивно-интервальных систем управления технологическими объектами в терминах интервального анализа. Пусть задан полностью управляемый и идентифицируемый объект управления вида
(1)
где:
=
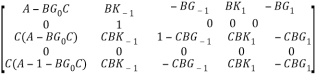
где 
-вектор состояния, 
вектор управления, A,B,C — матрицы параметров объекта управления, 
матрицы входов прямой и обратной связи, определяющие параметры дискретного адаптивного регулятора, 
— вектор уставок регулятора, 
векторный случайный процесс типа белого шума. Примем, что эталонная модель задается уравнениями вида (1), в которых вместо матриц 
представлены их значения на номинальном режиме, а все переменные, кроме входных воздействий g, f отмечены индексом «м».
Естественно, что коэффициенты реального управляемого объекта будут отличаться от расчетных (идентифицированных) в силу неизбежной погрешности измерений, неточности вычислений, изменения параметров с течением времени и ряда других факторов. Поэтому более реальным будет предположение, что при синтезе адаптивных регуляторов мы имеем дело с интервальной неопределенностью параметров объектов управления.
Будем полагать, что параметры объекта управления принадлежат некоторому априори заданному числовому диапазону:
(2)
где 
являются, соответственно, элементами матриц многосвязного объекта управления.
Цель адаптивно-интервального управления формулируется в терминах подцелей управления следующим образом:
(3)
(4)
и (или)
(5)
при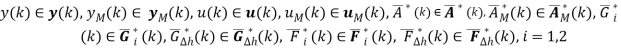 
Если выходным вектором является y, а входными q и f, то цели интервально-адаптивного управления в z — плоскости определяются интервальными тождествами:
(6)
(7)
Прямое применение интервальных методов (использование естественного интервального расширения в классической интервальной арифметике) не представляется возможным. Это объясняется некоторыми недостатками классической интервальной арифметики [2] (интервальной арифметики Каухера) и представления интервальных функций двумя граничными вещественными функциями позволяют, в определенном смысле упросить реализацию интервальных алгоритмов настройки.
В терминах интервального анализа определены понятия полной, слабой и частичной адаптируемости основного контура адаптивной системы управления. На основе цели адаптивно-интервального управления предлагаются интервальные статические адаптивные алгоритмы настройки регуляторов.
Bведены интервальные матрицы адаптируемости 
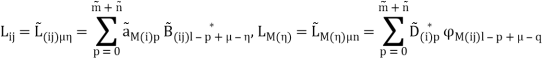
где: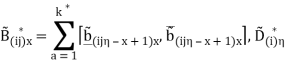 
=
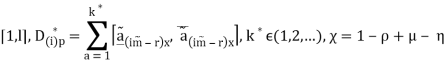
Зададим интервальные вектора 
в виде:
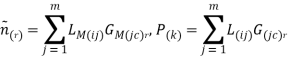
где:
, 
Показано, что искомые интервальные параметрыадаптивного регулятора определяются как решение матричного интервального линейного алгебраического уравнения:
(8)
где есть, в общем случае, прямоугольная интервальная матрица, блочными элементами которой являются интервальные матрицы адаптируемости L.
Далее, выше предложенный подход распространен на синтез адаптивных структурно-оптимизируемых регуляторов (на примере адаптивного апериодического регулятора) в случае, когда вместо канонического представления многомерных систем в пространстве состояний используется запись многомерной системы в пространстве передаточных функций. Рассмотрена возможность применения апериодическую регулятора при интервальной неопределенности параметров для адаптивных систем управления с неявной эталонной моделью.
Литература:
- Шарый С. П. Конечномерный интервальный анализ. — Новосибирск: Изд.: «XYZ» СО РАН. -2018. [Электрон. ресурс]. URL: http://interval.ict.nsc.ru /Library/InteBooks/SharyBook.pdf
- Алефельд Г., Херцбергер Ю. Введение в интервальные вычисления. — М.: Мир. — 1987. -262 с.
- Ядыкин И. Б. Оптимальная настройка линейных регуляторов // Докл. АН СССР. 1985 т. 285, № 3, с 574–577
