Известно, что софизмом называется умышленно ложное умозаключение, которое кажется правильным. Каков бы не был софизм, он обязательно содержит одну или несколько замаскированных ошибок. Особенно часто в математических софизмах скрыто выполняются запрещённые действия или не учитываются условия применимости теорем, формул и правил. Иногда рассуждения ведутся с использованием ошибочного чертежа или опираются на приводящие к ошибочным заключениям «очевидности». Встречаются софизм, содержащие и другие ошибки.
В истории развития математики софизмы играли существенную роль. Они способствовали повышению строгости в математических рассуждениях и содействовали более глубокому уяснению понятий и методов математики. Роль софизмов в развитии математики сходна с той ролью, какую играли непреднамеренные ошибки в математических доказательствах, допускаемые даже выдающимися математиками. Уяснение ошибок в математических рассуждениях часто содействовало развитию математики. Особенно поучительна в этом отношении история аксиома Евклида о параллельных прямых. Формулируется эта аксиома, так: «Через данную точку, лежащую вне данной прямой, можно провести только одну прямую, параллельную данной». Эту аксиому на протяжении более чем двух тысяч лет пытались доказать, т. е. вывести из остальных аксиом геометрии, многие выдающиеся математики разных времён и разных народов. Все эти попытки не увенчались успехом. Многочисленные «доказательства», какие были найдены, оказались ошибочными [3]. «Строгого доказательства сей истины», — писал великий русский математик Н. И. Лобачевский в 1823 году в своем учебнике геометрии, до сих пор не смогли сыскать; какие были даны, могут назваться только пояснением, но не заслуживают быть почтены в полном смысле математическими доказательствами» [1]. И всё же, несмотря на ошибочность этих доказательств, они принести пользу развитию геометрии. Были основательно выяснены связи между различными теоремами геометрии. Можно сказать, что эти «доказательства» подготовили одно из величайших открытий в области геометрии и всей математики- открытие новой неевклидовой геометрии. Честь этого открытия и разработка новой геометрии принадлежит великому русскому математику Н. И. Лобачевскому.
Н. И. Лобачевский и сам сначала пытался доказать аксиому о параллельных, но скоро понял, что этого сделать нельзя. В 1826 году он установил, что утверждение, выражаемое аксиомой о параллельных, при помощи остальных аксиом геометрии доказать нельзя. Путь, идя которым Лобачевский установил невозможность доказательства аксиомы параллельных, и привёл его к открытию новой геометрии. Это открытие прославило русскую математику [1].
Примеров подобного рода можно было бы привести несколько. Они убеждают в том, что преодоление ошибок в математических рассуждениях содействует развитию математики.
Чем же полезны софизмы для излучающихся математику? Что могут они дать?
Разбор софизмов, прежде всего развивает логическое мышление, т. е. прививает необходимых в жизни навыки правильного мышления.
Обнаружить ошибку в софизме это значит осознать ее, а осознание ошибки предупреждает повторение ее в дальнейшем в других математических рассуждениях.
Особенно важно, что разбор софизмов помогает сознательному усвоению изучаемого математического материала, развивает наблюдательность, вдумчивость и критическое отношение к тому, что изучается. Значит, математические софизм заставляют внимательно и настороженно продвигаться вперед, тщательно следить за точностью формулировок, правильностью записей за допустимостью обобщений, за законностью выполняемых операций. Всё это нужно и полезно. Как приятно бывает обнаружить ошибку в математическом софизме и тем как бы восстановить истину в её правах. И чем труднее софизм, тем больше удовлетворение доставляет разбор его. В этой статье приведены несколько софизмов. При разборе этих софизмов надо постараться самостоятельно найти содержащиеся в них ошибки и отчётливо понять их. Очень важно добиться отчётливого понимания ошибок, иначе софизмы будут бесполезны, и может быть даже вредны.
Задача: Всякий треугольник — равнобедренный [2].
Пусть АВС (рис. 1) — произвольный треугольник. Проведём биссектрису угла А и перпендикуляр к стороне ВС, проходящей через её середину D. Может оказаться так, что точке пересечения биссектрисы и перпендикуляра (К) будет лежать внутри треугольника АВС.
Опустим из точки К перпендикуляры КЕ и КF на стороны АС и АВ. Имеем ∆АЕК=∆ АFК, а значит КЕ = КFи АЕ=АF. Треугольники ВКD и СКD также равны, а поэтому КВ=КС. Остаётся рассмотреть прямоугольные треугольники ВКF и СКЕ. Они равны, так как КЕ = КF и АЕ=АF. Из равенства этих треугольников вытекает, что ЕС=FВ. Возьмём два равенства АЕ=АF и СЕ=ВF. Сложив их по частям, получаем АС=АВ. Аналогично можно провести рассуждения в случае, если точка К будет лежать вне треугольника АВС (рис.2).
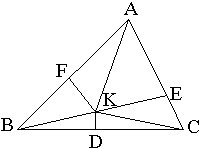
Рис. 1.
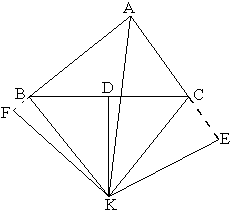
Рис. 2.
Рассуждения в случае, если точка К будет лежать на стороне ВС (совпадает с D), также не сложны. Во всех случаях, приходим к выводу, что треугольник АВС–равнобедренный. Значит, любой треугольник равнобедренный. Где ошибка?
Ответ: Единственный возможный случай, если треугольник АВС не является равнобедренным, иллюстрируется рисунком 3.
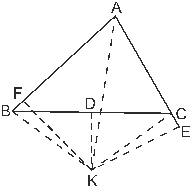
Рис. 3.
Также можно привести много различных примеров “например решения рациональных и иррациональных уравнений и неравенств”, при решении которых способствуют повышению строгости в математических рассуждениях и уяснениям понятий и методов математики.
Литература:
- Я. С. Дубнов «Ошибки геометрических доказательствах», Гостехиздать., 1953 г.
- В. И. Обреимов «Математические софизмы» Учпедгиз, Москва, 1957 г.
- В. Брадис и А. Харчева «Ошибки в математических рассуждениях», Учпедгиз, 1938 г.







