В этой работе приближенно решена смешанная задача для волнового уравнения методом разделения переменных, методом вариационных итераций и методом разложения Адомиана. Все эти методы обеспечивает последовательность функций, которая сходится к точному решению. Во всех случаях получены одинаковые результаты, но при этом метод разложения Адомиана являлся очень простим и удобным.
Ключевые слова: смешанная задача, волновое уравнение, метод разделения переменных, метод вариационных итераций, метод разложения Адомиана, начальное приближение, последовательность функций, точное решение.
Основной задачей строительной механики является разработка методов расчёта и получения данных для надёжного и экономичного проектирования зданий и сооружений. Надёжные методы расчётов таких зданий и сооружений позволяют возводить достаточно лёгкие и надёжные конструкции. Определённые математические модели и расчёты некоторых объектов строительной механики приводятся к решению линейных или нелинейных уравнений математической физики. В данной работе предложены применения современных более простых и точных методов решения таких уравнений [1–9].
Требуется точно решать следующую смешанную задачу для волнового уравнения методом разделения переменных (МРП), методом вариационных итераций (МВИ) и методом разложения Адомиана (МРА) [2, 7]:
, 
, (1)
, (2) 
. (3)
Для решения задачи примем обозначение 
. Из задачи (1)-(3) получим следующую задачу:
, (4)
, (5) 
. (6)
1) По идею МРП имеем:
. Подставляя это выражение к уравнению (4) имеем две уравнения вида [7]
.
Отсюда получим спектральную задачу: 
, 
.
При 
имеем
, 
и 
,
; а вторая 
.
Общее решение уравнение (4) и (5): 
,
a из условия (6) имеем 
,
k=2,3,4,…;
.
Точное решение задачи (4)-(6): 
.
2) Теперь уравнение (4) будем решать сначала по начальным условиям (6), а затем с граничными условиями (5) методом разложения Адомиана (МРА).
Для МРА имеем формулу приближенного решения задачи (4) и (6) [2]:
.
По идею МРА:
; 
; 
;
;…;
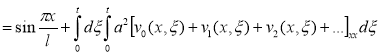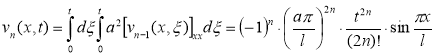и т. д.
Точное решение задачи (4) и (6): 
.
Для МРА имеем формулу приближенного решения задачи (4) и (5):
.
Здесь 
, (7)
По идею МРА:
;
; 
;
;…;
и т. д.
Общее решение уравнение (4), (5) и (7):
a из условия (6) имеем
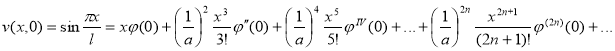
и т.д. 
.
Точное решение задачи (4)-(6): 
.
3) Уравнение (4) будем решать сначала по начальным условиям (6), а затем с граничными условиями (5) методом вариационных итераций (МВИ).
Для решения задачи (4)-(6) МВИ примем обозначение
(8)
Из уравнения (4) получим следующую интегро-дифференциальное уравнение:
, (9)
По идею МВИ имеем формулу приближенного решения задачи (9):
Здесь 
— множитель Лагранжа, а для стационарного случая 
, 
и отсюда имеем 
. Тогда имеем приближенную формулу
Применяя МВИ, получим следующие результаты:
; 
; 
и т. д.
Точное решение задачи (9):
a из обозначения (8) имеем 
Для решения задачи (4) и (5) МВИ примем обозначение 
(10).
Из уравнения (4) получим следующую интегро-дифференциальное уравнение:
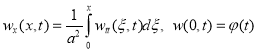, (11)
По идею МВИ имеем формулу приближенного решения задачи (11):
Здесь также . Тогда имеем приближенную формулу
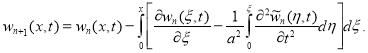
Применяя МВИ, получим следующие результаты:
; 
; 
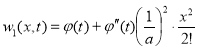и т. д.
Точное решение задачи (11):
a из обозначения (10) имеем 
a из условия (6) имеем
и т.д. .
Точное решение задачи (4)-(6): 
.
Точное решение задачи (1)-(3): 
.
Эти результаты проверены с помощью математического пакета Maple 17 [6].
Таким образом, МРП, МВИ и МРА дают одинаковые результаты, но МРА является более простим, точным и быстро приближающим к точному решению задачи. Поэтому в дальнейшем рекомендуется использование МРА при решении линейных и нелинейных задач математической физики [1–2, 8].
Литература:
- Adomian, G. Solving Frontier Problems of Physics: The Decomposition Method. Boston, MA: Kluwer, 1994.
- Wazwaz A. M. Partial Differential Equations and Solitary Waves Theory. Higher Education Press, Berlin Heidelberg, 2009. — 761 p.
- Абдурашидов А. А. Решения нелинейных волновых уравнений методом вариационных итераций // Международный научный журнал: Молодой ученый. — 2017. — № 6. — С. 4–8.
- Абдурашидов А. А. Точное решение некоторых нелинейных уравнений Гарднера упрощенным методом укороченных разложений // Международный сетевой научно-практический журнал: Наука среди нас. Выпуск № 2(6), 2018. — С. 35–46.
- Абдурашидов А. А., Касимова Ф. У., Рахимова Х. А. Приближенное решение волновых уравнений более высокого порядка методом вариационных итераций // Международный научный журнал: Развитие и актуальные вопросы современной науки, № 4 (4), 2017. — С. 4–9.
- Алексеев Е. Р., Чеснокова О. В. Решение задач вычислительной математики в пакетах Mathcad, Matlab, Maple (Самоучитель). — М.: НТ Пресс, 2006. — 496 с.
- Бицадзе А. В., Калиниченко Д. Ф. Сборник задач по уравнениям математической физики. Учеб. пособие для механико-математ. и физ. спец. вузов. — 2-е изд., доп. — М.: Наука, 1985. — 310 с.
- Кудряшов Н. А. Методы нелинейной математической физики: Учебное пособие. 2-е изд. — Долгопрудный: Интеллект, 2010. — 368 с.
- Полянин А. Д., Зайцев В. Ф., Журов А. И. Методы решения нелинейных уравнений математической физики и механики. — М.: ФИЗМАТЛИТ, 2005. — 256 с.
