В работе приведена математическая модель задачи Коши, основные идеи метода разложения Адомиана и метода вариационных итераций, а затем решены конкретные начальные задачи с уравнениями гиперболического типа.
Ключевые слова. задача Коши, волновое уравнение, метод вариационных итераций, метод разложения Адомиана, начальное приближение, последовательность функций, точное решение.
В настоящее время для решения практических задач механики активно используются различные современные аналитические и приближенные методы с применением вычислительной техники, в частности, наибольшее распространение получили приближенные методы: метод гомотопического анализа (HAM), метод гомотопического разложения (HPM), метод разложения Адомиана (ADM), метод вариационных итераций (VIM) и др., а также их различные модифицированные варианты [1–9]. В данной работе показаны возможности нахождения приближенных решений некоторых начальных задач. Сначала описывается математическая модель задачи Коши, основная идея метода разложения Адомиана и метода вариационных итераций [5], а затем рассмотрены решения конкретных начальных задач для уравнения гиперболического типа.
Требуется точно решать задачи Коши для n-мерного волнового уравнения методом вариационных итераций (VIM) и методом разложения Адомиана (ADM) [5].
Математическая модель задачи имеет вид
, (1) 
, (2)
где 
— точка в n-мерном пространстве; 
— оператор Лапласа; 
— неизвестная функция (функция волны); 
— заданные функции (форма и скорость волны при 
соответственно).
а) Для решения задачи (1) и (2) ADM воспользуемся соотношениями [5]:
.
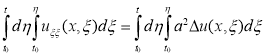
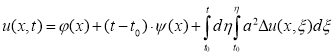По идею ADM:
; 
; 
;
;…;
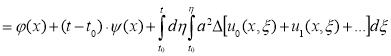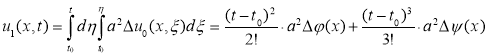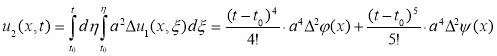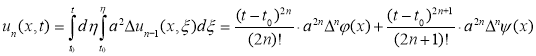и т. д.
Решение задачи (1) и (2) имеет вид:
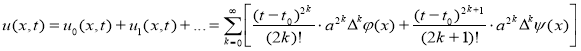. (3)
б) Для решения задачи (1) и (2) VIM воспользуемся следующей заменой:
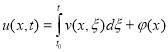. (4)
Тогда уравнение (1) приводится к следующему интегро-дифференциальному уравнению:
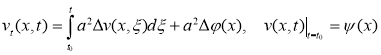. (5)
Для уравнения (5) приближенная формула VIM имеет вид [4]:
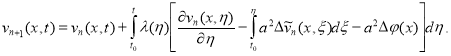
Здесь 
— множитель Лагранжа, а для стационарного случая 
, 
и отсюда имеем 
. Тогда имеем приближенную формулу вида
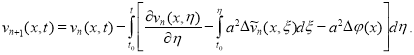
Применяя МВИ, получим следующие результаты:
; 
;
и т. д. Тогда решение уравнение (5) пишутся в виде
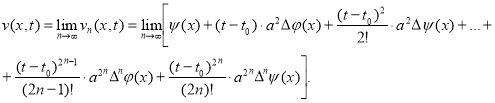
Учитывая замену (4) имеем
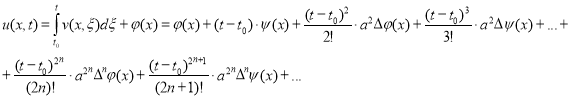
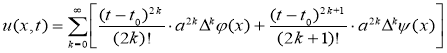. (3)
Для того чтобы проверят на равномерную сходимость этого ряда воспользуемся теоремой Вейерштрасса.
Теорема (Признак Вейерштрасса). Если каждый член функционального рядя
. (6)
удовлетворяет неравенства 
(n=1,2, …) в множестве 
и численный ряд 
сходящиеся, то функциональный ряд (6) будет равномерно сходящимся в множестве M [6].
Будем оценивать ряда (3):
.
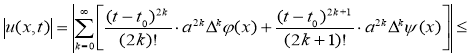
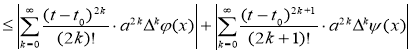Если функции 
в 
непрерывно и имеют производные достаточного порядка, то в момент 
времени t справедлива следующая оценка:
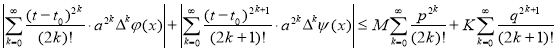, (7)
где M, K, p, q = const. Теперь будем проверять на равномерную сходимость рядов 
и 
. По признаку Даламбера о сходимости ряда с положительными членами имеем 
, аналогично имеем 
. Тогда числовые ряди и также будет сходящимся. Отсюда по справедливости оценки (7) и по признаку Даламбера ряд (3) будет сходящимся. Исходя из этого функция 
является решением волнового уравнения (1) задачи Коши. Теперь будем применят формулу (3) в следующих примерах.
Пример 1. Найти решение следующего однородного трехмерного волнового уравнения задачи Коши [7]: 
.
Решение. Для решения данной задачи воспользуемся формулой (3):
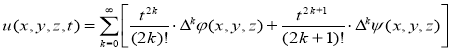
Тогда решение заданной задачи имеет вид:
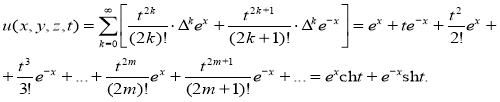
Пример 2. Найти решение неоднородного трехмерного волнового уравнения задачи Коши: 
, 
.
Решение. Для решения данной задачи введем обозначение вида:
Тогда получим следующую начальную задачу:
, 
, 
Для решения данной задачи воспользуемся формулой (3):
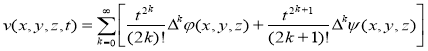
Тогда решение вспомогательной задачи имеет вид:
.
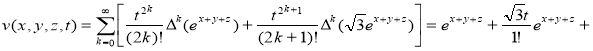
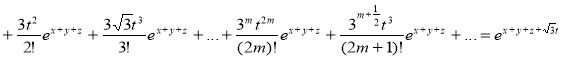Окончательно имеем решение вида 
.
Таким образом, в данной работе рассмотрена начальная задача для уравнения гиперболического типа. Решения задач Коши строились с помощью метода разложения Адомиана и метода вариационных итераций.
Литература:
- Abdirashidov A., Kadirov N. X., Ortikov B. B., Abdurashidov A. A. Exact solution of fractional diffusion equations using the variational iteration method and Adomian decomposition method // International Scientific Journal «Theoretical & Applied Science», № 5, 2018. P.101–107.
- Abdurashidov A. A., Ortiqov B. B., Qadirov N. X., Abdirashidov A. Exact solution of nonlinear equations Burgers-Huxley, Korteweg-de Vries-Burgers and Klein-Gordon using the modified simple equation method // International Scientific Journal «Theoretical & Applied Science», № 3, 2018. P.101–107.
- Adomian, G. Solving Frontier Problems of Physics: The Decomposition Method. Boston, MA: Kluwer, 1994.
- Wazwaz A. M. Linear and Nonlinear Integral Equations. Higher Education Press, Berlin Heidelberg, 2011. — 658 p.
- Wazwaz A. M. Partial Differential Equations and Solitary Waves Theory. Higher Education Press, Berlin Heidelberg, 2009. — 761 p.
- Азларов Т. А., Мансуров Х. Математический анализ. II часть. — Ташкент: “Ўқитувчи”, 1989. — 424 с.
- Бицадзе А. В., Калиниченко Д. Ф. Сборник задач по уравнениям математической физики. Учебное пособие. — 2-е изд., доп. — М.: Наука, 1985. — 310 с.
- Ибрагимов Н. Х. Практический курс дифференциальных уравнений и математического моделирования.- Нижний Новгород: Изд-во Нижегородского госунив.-та, 2007.-421 с.
- Кудряшов Н. А. Методы нелинейной математической физики: Учебное пособие. 2-е изд. — Долгопрудный: Интеллект, 2010. — 368 с.
