В основе криптографических систем с открытым ключом лежит теория необратимых (односторонних) функций.
Определение. Функция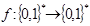 
называется односторонней, если, во-первых, она вычисляется за полиномиальное время, а, во-вторых, для любого полиномиального вероятностного алгоритма 
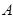существует исчезающе малая функция 
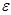такая, что 
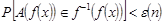, где вероятность берется равномерному выбору 
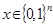и броскам монетки при выполнении .
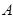Приведем основные свойства, которыми обладают односторонние функции:
1) Если известно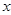 
, то вычисление 
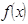однозначная задача;
2) Если известно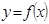 
, то сложность 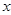неопределенно возрастает.
В основу криптографической системы с открытым ключом RSA находится задача умножения и разложения составных чисел на простые множители, которая является вычислительно однонаправленной задачей.
В криптографической системе с открытым ключом каждый участник имеет в своем распоряжении как открытым ключ (англ. publickey), так и секретным ключ (англ. secretkey). Каждый ключ — это часть информации. В состав ключа, используемого в криптографической системе RSA, входит пара, принадлежащая множеству целых чисел. Каждый участник создаёт свой открытый и секретный ключ самостоятельно. Секретный ключ каждый из них держит в секрете, а открытые ключи можно сообщать, кому угодно или даже публиковать их. Открытый и секретный ключи каждого участника обмена сообщениями образуют «согласованную пару», которая относительно друг друга взаимообратная.
На состояние 2009 года система шифрования RSA считается надежной уже с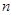 
равной 1024 бита. Исследовательские группы из Европы, Азии и Америки успешно решили задачу по расшифровке данных при помощи криптографического ключа RSA длинной 768 бит. По словам исследователей, после их работы в качестве надежной системы шифрования можно рассматривать только RSA-ключи длиной 1024 бита и более. Причём от шифрования ключом длиной в 1024 бит стоит отказаться в ближайшие три-четыре года.[1] На первый шаг (выбор пары полиномов степени 6 и 1) было потрачено около полугода вычислений на 80 процессорах, что составило около 3 % времени, потраченного на главный этап алгоритма (просеивание), который выполнялся на сотнях компьютеров в течение почти двух лет. Если интерполировать это время на работу одного процессора AMD Opteron 2.2ГГц с 2Гб памяти, то получилось бы порядка 1500 лет. Обработка данных после просеивания для следующего ресурсоёмкого шага (линейной алгебры) потребовалось несколько недель на малом количестве процессоров. Заключительный шаг после нахождения нетривиальных решений ОСЛУ занял не более 12 часов.
Решение ОСЛУ проводилось методом Видемана на нескольких раздельных кластерах и длилось чуть менее 4 месяцев. Размерность матрицы при этом оказалась 192 796 550х192 795 550 при наличии 27 795 115 920 ненулевых элементов (то есть в среднем 144 ненулевых элементов на строку). Для хранения матрицы на жёстком диске понадобилось около 105 гигабайт. В то же время понадобилось около 5 терабайт сжатых данных для построения данной матрицы.
Группе ученых удалось вычислить 232-цифровой ключ, открывающий доступ к зашифрованным данным. Исследователи уверены, что используя их метод факторизации, взломать 1024-битный RSA-ключ будет возможно.
Зная разложение 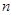на произведение двух простых чисел, злоумышленник сможет определить секретную экспоненту 
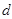и взломать RSA.
Далее рассмотрим несколько элементарных атак и проиллюстрируем возможные проблемы при не корректном использовании алгоритма шифрования RSA. [2].
Прежде всего, на случайные числа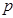 
и 
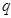необходимо наложить следующие ограничения:
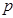· и 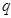не должны быть слишком близки друг к другу, т.к. они в таком случае могут себя скомпрометировать;
· Необходимо вибирать «сильные» простые числа, чтобы нельзя было воспользоваться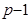 
методом Полларда.
Схема с общим модулем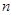
Для предотвращения генерации модулей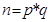 
для каждого пользователя, сервер использует один 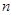для шифрования информации. Сторона 
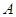использует этот сервер для получения сообщения 
.
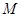Злоумышленник хочет расшифровать сообщение стороны 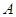. Шифротекст 
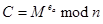, отправленный стороне 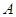, не может быть расшифрован стороной 
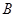, если она не обладает секретным ключом 
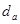. Однако сторона 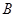может использовать свои экспоненты 
, 
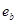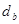, чтобы разложить модуль 
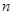, и после этого, зная 
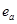, вычислить секретную экспоненту .
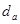Для каждого пользователя должен использоваться свой модуль .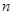
Атака на подпись RSA в схеме с нотариусом
Пусть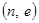 
- открытый ключ нотариуса. Злоумышленник получает отказ при попытке подписаться у нотариуса сообщения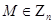 
Злоумышленник стремится определить подпись нотариуса на сообщении 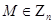. Противник выбирает случайное 
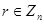и находит 
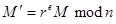. После чего он посылает это сообщение на подпись к нотариусу. Если данная схема оканчивается успехом, то 
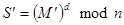и злоумышленник (вычислив 
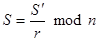) получает подпись сообщения .
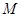В процессе подписи можно добавлять некоторое случайное число в сообщение.
Малые значения секретной экспоненты
Чтобы увеличить скорость расшифрования (или создания цифровой подписи) было уменьшено число ненулевых битов двоичного представления секретной экспоненты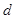 
.
Вычислить секретную экспоненту 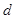. В 1990 году Михаэль Винер (Michael J. Wiener) показал, что в случае малого значения 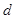возможен взлом системы RSA.
Теорема (Винера). Пусть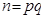 
, где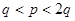 
=> 
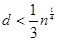. Тогда, если известно 
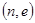, где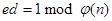 
, то существует эффективный способ нахождения .
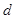Таким образом, если n имеет размер 1024 бита, необходимо чтобы d был не менее 256 бит длиной.
Малые значения открытой экспоненты
Для увеличения скорости шифрования и проверки цифровой подписи, используют малые значения открытой экспоненты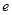 
. Но для повышения криптостойкости RSA, рекомендовано брать 
.
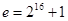Атака Хастада
Сторона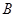посылает зашифрованное сообщение 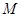нескольким пользователям (допустим 
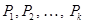). Каждый пользователь имеет свой открытый ключ 
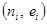, причем 
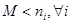. Сторона 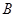шифрует сообщения с применением очередного открытого ключа каждого пользователя. После чего сообщения посылаются соответствующему адресату. Злоумышленник подключается к каналу передачи данных и собирает 
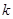зашифрованных сообщений.
Противник стремится восстановить сообщение М. Действительно, предположим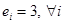 
, тогда противник может восстановить 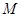, если 
.
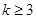Приведем доказательство данного утверждения.
Если злоумышленник определил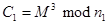 
, 
, 
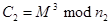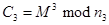и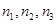 
взаимно просты (иначе система RSA не выполнялась бы). Применяя китайскую теорему об остатках к 
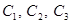можно получить 
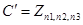. Поскольку 
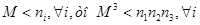и 
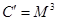. Следовательно злоумышленник может восстановить сообщение вычислив кубический корень из 
.
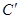Данная атака возможна только при малых значениях секретной экспоненты 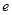. Мерой защиты в данной ситуации может служить, применение произвольной перестановки.
Атака Франклина-Рейтера
Имеются два сообщения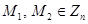 
, причем 
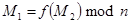, где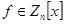 
- открытый многочлен. Сторона 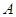с открытым ключом 
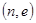получает эти сообщения от стороны 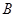, которая зашифровывает сообщения и передает полученную зашифрованную информацию 
.
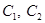Рассмотрим следующее. Злоумышленник имеет параметры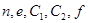 
и стремится найти 
.
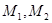Имеет место, следующее утверждение: Пусть 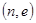– это открытый ключ системы RSA, а 
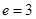. Так же 
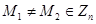и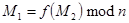 
, имея линейный многочлен следующего вида 
, 
.
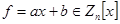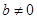Отсюда следует что, имея набор параметров 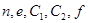, можно определить 
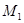и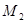 
.
Докажем данное утверждение. Действительно для любого :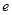 
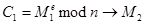существуют корни многочлена 
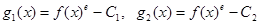. Таким образом оба многочлена делятся на 
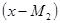. Злоумышленник может использовать алгоритм Евклида для нахождение НОД 
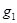и
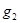. Следовательно при 
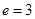и если НОД
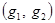есть линейный многочлен, то можно эффективно определить 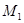и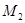 
.
Мерой противодействия атаке Франклина-Рейтера может служить увеличение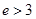 
. В данном случае время взлома системы становится пропорциональным 
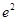, следовательно, эта атака может быть использована только при малых значениях открытой экспоненты.
Так же данные атаки возможны при нарушении процедуры аутентификации [3]. Чтобы переслать секретную информацию, зашифрованную открытым ключом, отправитель, прежде всего, должен убедиться, что информация дойдет до адресата. Так же существует необходимость создания защищенных каналов связи для передачи ключей. Однако в криптографии с открытым ключом выполняется условие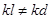 
. Следовательно, в общем случае организация секретного канала передачи ключей шифрования сводится к задаче аутентификации.
Литература:
1. Cryptology ePrint Archive: Report 2010/006 [Электронный ресурс]: ресурс содержит разнообразную информацию в области криптографии – Электрон. дан.– Режим доступа: http://eprint.iacr.org/2010/006.pdf, свободный. – Factorization of a 768-bit RSA modulus.– Яз. англ.
2. Смарт Н. Криптография М: Техносфера, 2003 – 528 с.
3. Венбо Мао Современная криптография. Теория и практика = Modern Cryptography: Theory and Practice. — М.: Вильямс, 2005. — 768 c.
