Методика работы с сюжетной задачей: смысловое чтение и этапы решения



В статье уточнён смысл этапов работы с текстом, выделенных в программе «Основы смыслового чтения и работа с текстом»; указано соответствие этапов смыслового чтения с этапами решения математических задач согласно Д. Пойа; перечислены некоторые приёмы работы над условием сюжетной задачи, приведены соответствующие примеры.

Ключевые слова: УУД, смысловое чтение, математическая задача, сюжетная задача.

В Федеральном государственном образовательном стандарте основного общего образования (ФГОС ООО) подчеркивается важность реализации одной из междисциплинарных учебных программ обучения учащихся — «Основы смыслового чтения и работа с текстом». Цель смыслового чтения состоит в максимально точном и полном понимании содержания текста, улавливания всех его деталей и практическом осмыслении извлеченной информации.

В концепции формирования универсальных учебных действий обучающихся основной школы (авторов А. Г. Асмолова, Г. В. Бурменской и др. [1]) наряду со многими универсальными действиями выделены действия смыслового чтения. Смысловое чтение включает в себя умение осмысливать цели и задачи чтения, умение находить и извлекать информацию из различных текстов, работать с разными видами текста, понимать и адекватно оценивать информацию из текста. Одним из результатов изучения математики является умение работать с математическим текстом, в частности с текстом математической задачи.

Интерпретируем суть этапов работы с текстом, выделенные в программе «Основы смыслового чтения и работа с текстом» [4], относительно текста математической задачи:

1) поиск информации и понимание прочитанного (ориентирование в содержании текста задачи и понимание её смысла) включает в себя следующие действия:

– определять тип задачи, основную проблему задачи;

– формулировать тезис, выражающий смысл текста задачи (выделять основные ситуации, рассматриваемые в задаче);

– находить в тексте известные и неизвестные величины (данные);

– выполнять смысловое свёртывание выделенных фактов, действий;

– формировать на основе анализа текста задачи систему аргументов для обоснования ее решения;

– организовывать поиск информации, необходимой для решения задачи;

– выполнять чтение задачи, представленной в наглядно-символической форме (рисунка, таблицы, диаграммы, схемы).

2) преобразование и интерпретация информации включает в себя следующие действия: преобразовывать текст, используя новые формы представления информации: формулы, графики, диаграммы, таблицы (в том числе динамические, электронные, в частности в практических задачах), переходить от одного представления данных к другому.

3)оценка информации включает в себя следующие действия:

– связывать информацию, обнаруженную в тексте задачи с раннее известными знаниями и решёнными задачами;

– оценивать способы и методы решения задачи;

– на основе имеющихся знаний, жизненного опыта подвергать сомнению достоверность имеющейся информации в задаче, обнаруживать недостоверную информацию, недостаток информации и находить пути его восполнения;

– в процессе работы с задачей выявлять содержащуюся в ней противоречивую, конфликтную информацию;

– находить способы проверки противоречивой информации, определять достоверную информацию.

При работе с математической задачей, согласно Д. Пойа [2] выделяют 4 этапа:

1) работа с условием задачи;

2) составление плана решения задачи;

3) реализация плана решения задачи;

4) «взгляд назад» — этап изучения найденного решения задачи.

Сопоставим данные этапы с этапами смыслового чтения (Табл. 1).

Таблица 1

Соответствие этапов смыслового чтения сэтапами решения математических задач

Этапы смыслового чтения	Этапы решения математических задач
Поиск информации и понимание прочитанного	I. Работа с условием задачи: запись условия и требования задачи (таблица, рисунок, схема); формулирование проблемы и цели решения задачи.
	II. Составление плана решения задачи: анализ данных задачи; составление плана решения задачи; рассмотрение различных ситуаций; выдвижение гипотезы решения; выявление, сопоставление и оценка способов решения задачи; построение цепочки умозаключений, рассуждений.
Преобразование и интерпретация информации	III. Осуществление плана решения задачи: выбор способа записи решения задачи, корректировка его правильности; оформление решения задачи.
Оценка информации	IV. Этап изучения найденного решения: соотнесение действий с условием и требованием задачи; обобщение, конкретизация полученных результатов; оценка возможности использования полученных данных при решении других задач.

Работа по обучению учащихся решению сюжетных задач начинается с выделения структуры задачи: условия и требования. При этом в условии определяются объекты предметной области, а после этого — отношения между объектами.

Можно выделить следующие приёмы работы над условием:

– краткая запись с обозначением наименований и постановкой вопроса;

– запись таблицей;

– графическая иллюстрация;

– запись-перечень (при решении задачи методом уравнений).

Основным затруднением, которое может возникнуть у обучающихся при работе над условием задачи — невозможность выделить в условии величины, связанные зависимостями. Этому могут служить две причины: 1) у учеников не сформировано представление о нужной зависимости; 2) представление сформировано, но нужные зависимости не определены в условии.

В методике обучения решению сюжетных задач предлагаются различные пути преодоления указанного затруднения. Один из них — выполнение упражнений, которые можно условно разбить на 2 группы. Покажем, как можно построить работу над условием задачи и приведём примеры таких упражнений на основе следующей задачи:

Задача 1. Первая труба пропускает на 10 литров воды в минуту меньше, чем вторая труба. Сколько литров воды в минуту пропускает первая труба, если резервуар объёмом 60 литров она заполняет на 3 минуты дольше, чем вторая труба? [3]

I группа упражнений.

1. Прочтите условие задачи и ответьте на вопросы.

Первая труба пропускает на 10 литров воды в минуту меньше, чем вторая труба.

Сколько литров воды в минуту пропускает первая труба, если резервуар объёмом 60 литров она заполняет на 3 минуты дольше, чем вторая труба?

а) Назовите величины, которые связаны зависимостями:

– одна больше другой на 10

– одна меньше другой на 10

б) Если первая труба пропускает x литров воды в минуту, то как можно истолковать выражения: x + 10; 60/x; 60/(x + 10)?

2. Используя справочный материал, заполните пропуски в тексте задачи.

Первая труба пропускает___________________________, чем вторая труба. Сколько литров воды в минуту пропускает первая труба, если резервуар объёмом _____________ она заполняет ______________ __________, чем ____________?

Справочный материал: 60 литров, вторая труба, на 10 литров воды в минуту меньше, на 3 минуты дольше.

II группа упражнений.

1. Прочтите условие задачи и определите, какие из следующих выражений имеют смысл, если первая труба пропускает 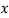литров воды в минуту.

Выражения: 60/10; 60/(x + 10); 10 + 3; 60/x.

2. Заполните пропуски в тексте задачи, если известно, что её решение сводится к уравнению: 60/x — 60/(x + 10) =3.

Первая труба пропускает _______________________ меньше, чем вторая труба. Сколько литров воды в минуту пропускает первая труба, если резервуар ________________ она заполняет на _________________, чем вторая труба?

На уроках такие упражнения целесообразно предлагать систематически.

Кроме указанных приёмов работы над условием задачи, можно выделить приёмы работы после решения задачи, а именно:

1. составление аналогичной задачи (со сменой сюжета);
2. составление обратной задачи;
3. решение задачи другим способом.

На примере Задачи 1 покажем, как можно реализовать 1 и 2 из перечисленных выше приёмов работы после решения.

1. Составление аналогичной задачи

В 307 году до нашей эры Эпикур создал свою школу в Афинах и в день её открытия пригласил на торжество много гостей. На пиру вино лилось из двух труб. Среди множества гостей, приглашённых Эпикуром, был математик. Он заметил, что первая труба пропускает на 10 литров вина в минуту меньше, чем вторая труба, и задался вопросом: сколько литров вина в минуту пропускает первая труба, если 60 карасов по 1 литру она заполняет на 3 минуты дольше, чем вторая труба? После двух выпитых кубков вина математик посчитал, что первая труба пропускает 19 литров вина в минуту. Правильно ли он посчитал? Если нет, давайте ему поможем.

2. Составление обратной задачи

Первая труба, пропуская 10 литров воды в минуту, заполняет резервуар объёмом 60 литров на 3 минуты дольше, чем вторая труба. На сколько литров воды в минуту больше пропускает вторая труба, чем первая?

Таким образом, о достаточно полном понимании содержания сюжетной задачи могут свидетельствовать следующие умения:

– общая ориентация в содержании текста задачи и понимание его целостного смысла (определение типа задачи; выделение ситуаций, рассматривающихся в задаче; формулирование проблемы, цели задачи и т. д.);

– нахождение информации (умение выделять условие и требование задачи, известные и неизвестные величины, избыточные и недостающие данные задачи; умение находить способ решения задачи и т. д.);

– интерпретация текста (умение представлять сюжетную задачу в виде табличной модели, в виде рисунка, схемы и др.; делать выводы, выводить следствия из условия задачи, строить аргументированные выводы; правильно оформлять решение сюжетной задачи и т. д.);

– рефлексия содержания текста задачи и ее решения (умение связывать информацию, обнаруженную в тексте задачи с имеющимися знаниями; оценить рациональность решения задачи и т. д.).

Литература:

1. Асмолов А. Г. Формирование универсальных учебных действий в основной школе: от действия к мысли. Система заданий. Пособие для учителя // Асмолов А. Г., Бурменская Г. В., Володарская И. А. — М.: Просвещение, 2013. — 159 с.
2. Высоцкий И. Р. Математика. 3 модуля. Основной государственный экзамен. 50 вариантов типовых заданий / И. Р. Высоцкий, Л. О. Рослова, Л. В Кузнецова и др.; под ред. И. В. Ященко. — М.: Издательство «Экзамен», 2016. — 295 с.
3. Пойа Д. Как решать задачу? — Львов: Квантор,1991. — 216 с.
4. «Примерная основная образовательная программа основного общего образования» (одобрена решением федерального учебно-методического объединения по общему образованию, протокол от 08.05.2015 № 1/15) (ред. От 28.10.2015)
5. Заир Бек С. И., Муштавинская И. В. — М.: Просвещение, 2011. — 223 с.