Рассматривается влияние факторов производства на оптимальный выпуск продукции. Анализ проводится в условиях, когда наблюдается влияние одного из двух факторов и ресурсы расходуются полностью в условиях предпочтения выпуска продукции второго вида.
Ключевые слова: задача об использовании ресурсов, минимальная норма выпуска продукции, минимальная относительная норма выпуска продукции двух видов, относительный расход ресурса в продукции, относительный расход одного ресурсов данного вида продукции, оценка влияния фактора на доход предприятия, предпочтение выпуска продукции одного вида к другому.
Анализ производства является одной из важных составляющих в выработке решений по эффективной деятельности предприятия. Его можно проводить, используя математические модели. В статье [1] была представлена одна из таких математических моделей предприятия, выпускающего два вида продукции и использующего три вида ресурсов [1, стр. 9, 13]. В статье [2] рассматривается модель производства продукции двух видов с использованием двух ресурсов. В этой статье даётся решение задачи оптимального выпуска продукции и эффективного использования ресурсов как решения пары двойственных задач линейного программирования. В работах [3–9] рассматривается влияние различных факторов производства: минимальной нормы выпуска продукции различных видов, спроса на продукцию разных видов. В частности, в работах [3, 4, 6, 7 и 9] рассматривается влияние минимальных относительной и абсолютной норм выпуска продукции, в работах [5 и 8] — относительного и абсолютного спроса на выпускаемую продукцию. На основе решения двойственных задач в статье [3] и в статьях [4, 6, 7 и 9] находятся возможные переходы решений в зависимости от направленности производственной деятельности по признаку предпочтения выпуска продукции какого-нибудь вида ([3, стр. 26]).
Постановка проблемы. Целью данной статьи является поиск перехода решения задачи, в которой предполагается влияние одного из двух факторов, рассмотренных в статьях [3, 4, 6, 7 и 9] и полного потребления обоих ресурсов при оптимальном плане. Условия, при которых анализируется проблема, предполагают, что есть предпочтение выпуска продукции второго вида.
В статье [3, стр. 25] были определены вспомогательные коэффициенты математической модели k1, k2, k, β1, β2, β, с помощью которых проводится анализ решения поставленной задачи. Эти коэффициенты также использовались в работах [4–9]. При определении коэффициентов полагается, что k1<k2 и β1<β2.
Предполагаем, что мы находимся в условиях производства, которые были определены в работе [3], а также производство предполагает предпочтение второго вида продукции по отношению к первому виду. Это означает, что коэффициент k>k2.
Методы проведения эксперимента. Висследовании поставленной задачи будем использовать методологию математического моделирования и методы анализа решения задач линейного программирования с помощью теории двойственности.
Описание результатов. В [3] было показано, что решение пары двойственных задач, в которых наблюдается влияние минимальной нормы n и полностью расходуются два ресурса, удовлетворяют системам следующих условий [3, стр. 35].
В прямой задаче [3, стр. 35] В двойственной задаче [3, стр. 35]:
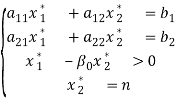 .(1)
.(1)
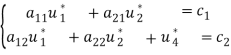 .(2)
.(2)
Решением будут значения: u1*=![]() , u2*=
, u2*=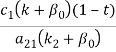 , u3*=0, u4*=
, u3*=0, u4*=![]() , где 0≤t≤1 и
, где 0≤t≤1 и ![]() 0 [3, стр. 35–36].
0 [3, стр. 35–36].
Найдём условия на параметр t, когда k>k2. Тогда ![]() <
< ![]() =0. Для последнего условия получаем:
=0. Для последнего условия получаем: ![]() <
< ![]() . Это противоречит условию
. Это противоречит условию ![]() . При k>k2 двойственная задача решения не имеет. Влияния минимальной нормы n на оптимальное решение пары двойственных задач нет.
. При k>k2 двойственная задача решения не имеет. Влияния минимальной нормы n на оптимальное решение пары двойственных задач нет.
Из [3] для решения задачи с влиянием минимальной относительной нормы β0 и полным расходом обоих ресурса выполняется [3, стр. 31]:
в прямой задаче [3, стр. 31] в двойственной задаче [3, стр. 31]:
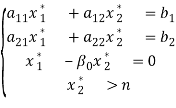 ,(3)
,(3)
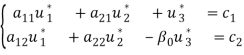 .(4)
.(4)
Решением двойственной задачи: u1*=![]() , u2*=
, u2*=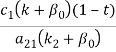 , u3*=
, u3*=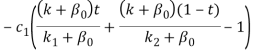 , u4*=0, где 0≤t≤1 и
, u4*=0, где 0≤t≤1 и ![]() [3, стр. 31–32].
[3, стр. 31–32].
При k>k2: ![]() >
>![]() = 1,
= 1, ![]() >
>![]() =1. Получаем:
=1. Получаем: ![]() >1. Неравенство автоматически выполняется при k>k2. При k>k2 решение двойственной задачи: u1*=
>1. Неравенство автоматически выполняется при k>k2. При k>k2 решение двойственной задачи: u1*=![]() , u2*=
, u2*=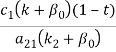 , u3*=
, u3*=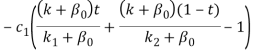 , u4*=0, где 0≤t≤1. Если t=0, то u1*=
, u4*=0, где 0≤t≤1. Если t=0, то u1*=![]() u2*=
u2*=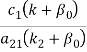 >
>![]() , u3*=
, u3*=![]() , u4*=0. Решение совпадает с решением задачи, в которой наблюдается влияние минимальной относительной нормы β0 и полностью расходуются второй ресурс. Если t=1, то u1*=
, u4*=0. Решение совпадает с решением задачи, в которой наблюдается влияние минимальной относительной нормы β0 и полностью расходуются второй ресурс. Если t=1, то u1*=![]() >
>![]() ,
,![]() u2*=0, u3*=
u2*=0, u3*=![]() , u4*=0. Решение совпадает с задачей, в которой есть влияние минимальной относительной нормы β0 и полностью расходуются первый ресурс.
, u4*=0. Решение совпадает с задачей, в которой есть влияние минимальной относительной нормы β0 и полностью расходуются первый ресурс.
Выводы. Приприоритетном выпуске второго вида продукции минимальная норма n не влияет на оптимальное решение задачи. Решение двойственной задачи, когда наблюдается влияние минимальной относительной нормы β0 и полностью расходуются оба ресурса, переходит в решение одной из двойственных задач. В первой задаче есть влияние минимальной относительной нормы β0 и полностью расходуется второй ресурс (t=0), а во второй задаче наблюдается влияние минимальной относительной нормы β0 и полностью расходуется первый ресурс (t=1).
Литература:
- О. В. Мамонов. Анализ использования двух ресурсов предприятия с двумя видами продукции с помощью графического способа решения задачи линейного программирования// Агропродовольственная экономика: научно-практический электронный журнал. Нижний Новгород: НОО «Профессиональная наука» — No10–2016. — 7–42 с.
- О. В. Мамонов. Анализ использования двух ресурсов предприятия с двумя видами продукции с помощью графического способа решения задачи линейного программирования// Агропродовольственная экономика: научно-практический электронный журнал. Нижний Новгород: НОО «Профессиональная наука» — No12–2016. — 30–62 с.
- О. В. Мамонов. Бикеева М. В. Решение задачи об использовании двух ресурсов для предприятия, выпускающего два вида продукции, с учётом влияния минимальной относительной нормы производства одного вида продукции к другому и минимальной нормы выпуска продукции второго вида// Агропродовольственная экономика: научно-практический электронный журнал. Нижний Новгород: НОО «Профессиональная наука» — No3–2018. — 22–41 с.
- О. В. Мамонов, А. В. Конюхова. Определение зависимости предельной полезности ресурса и оценок влияния факторов производства от минимальной нормы производства второго вида продукции/ Актуальные проблемы агропромышленного комплекса: сб. трудов научно-практической конференции преподавателей, студентов, магистрантов и аспирантов Новосибирского государственного аграрного университета (г. Новосибирск, 16–17 октября 2017 г.), выпуск 2. / Новосиб. гос. аграр. ун-т. — Новосибирск: ИЦ «Золотой колос», 2017. — с. 244–246
- О. В. Мамонов, Р. В. Луцик. Пример расчёта оценки влияния спроса на доход предприятия с двумя ресурсами: сб. трудов научно-практической конференции преподавателей, студентов, магистрантов и аспирантов Новосибирского государственного аграрного университета (г. Новосибирск, 16–17 октября 2017 г.), выпуск 2. / Новосиб. гос. аграр. ун-т. — Новосибирск: ИЦ «Золотой колос», 2017. — с. 246–249.
- О. В. Мамонов, А. В. Конюхова. Влияния технологических факторов производства в случае использования двух ресурсов/ Теория и практика современной аграрной науки: сб. национальной (всероссийской) научной конференции (г. Новосибирск, 20 февраля 2018 г.) / Новосиб. гос. аграр. ун-т. — Новосибирск: ИЦ «Золотой колос», 2017. — с. 546–550.
- О. В. Мамонов, А. В. Конюхова. Карта влияния факторов производства для предприятия, использующего один ресурс/ Роль аграрной науки в устойчивом развитии сельских территорий: Сб. II Всероссийской (национальной) научной конференции (г. Новосибирск, 25 декабря 2017 г.) / Новосиб. гос. аграр. ун-т. — Новосибирск: ИЦ «Золотой колос», 2017. — 817–822 с.
- О. В. Мамонов, С. В. Егорова, А. А. Пугачёва. Влияние спроса продукции двух видов и запаса ресурса на эффективность производства/Теория и практика современной аграрной науки: сб. национальной (всероссийской) научной конференции (г. Новосибирск, 20 февраля 2018 г.) / Новосиб. гос. аграр. ун-т. — Новосибирск: ИЦ «Золотой колос», 2017. — с. 542–546.
- А. В. Конюхова О. В., Мамонов. Анализ решения задачи о влиянии минимальной относительной нормы одного вида продукции к другому виду продукции, минимальной нормы второго вида продукции в случае баланса влияния обоих факторов, использования обоих ресурсов при приоритете выпуска второго вида продукции/ Актуальные направления развития аграрной науки в работах молодых учёных: сборник научных статей молодых ученых, посвященный 190-летию опытного дела в Сибири, 100-летию сельскохозяйственной науки в Омском Прииртышье и 85-летию образования Сибирского НИИ сельского хозяйства. ФГБНУ «Омский АНЦ». — Омск: ЛИТЕРА, 2018. — 194–198 с.







