В статье закон фильтрации берется в более общем виде. Для этого в формуле ![]() от
от ![]() нужно использовать кубическое слагаемое. При этом увеличивается точность при обработке индикаторных линий. Однако это необходимо также и для учета неравновесных свойств фильтрационного потока и влияния инерционных сил.
нужно использовать кубическое слагаемое. При этом увеличивается точность при обработке индикаторных линий. Однако это необходимо также и для учета неравновесных свойств фильтрационного потока и влияния инерционных сил.
Полученная таким образом формула, с одной стороны, будет содержать в себе закон Дарси, закон Форхгеймера а, с другой стороны, — позволит учесть неравновесность фильтрационного потока. [1–4]
При решении этих уравнений получаются формулы, подобные формулам закона Дарси и Дюпюи, которые учитывают влияние начального градиента и инерционных сил.
Ключевые слова: скорость, инерционные силы, начальный градиент, неравновесность.
In the article, the law of filtration is taken in a more general form. To this end, we must use the cubic summand in the formula ![]() of
of ![]() . This increases the accuracy when processing the indicator lines. However, this is also necessary to take into account the nonequilibrium properties of the filtration flow and the influence of inertial forces.
. This increases the accuracy when processing the indicator lines. However, this is also necessary to take into account the nonequilibrium properties of the filtration flow and the influence of inertial forces.
Thus obtained formula, on the one hand, will contain the law of Darcy, the law of Forchheimer, on the other hand, will allow to take into account the nonequilibrium filtration flow. [1–4]
Solving this equation, we obtain a formula similar to the Dupuis formula, which takes into account the influence of the initial gradient and inertial forces.
In the article, a graph of the change in the rate of depletion form depression is obtained and a methodology for interpreting such indicator lines are shown.
Keywords: speed, inertial forces, initial gradient.
Во время фильтрации неравновесной жидкости преобладающую роль начинают играть упругие силы, так как вязкие силы, обуславливающие сопротивление, являются решающим фактором лишь в области малых скоростей фильтрации и заметно снижаются с ее увеличением. При этом жидкость не успевает релаксировать при переходе из одной поры в другую. Это приводит к увеличению эффективной вязкости, так как фактор сопротивления с увеличением скорости возрастает быстрее, чем скорость фильтрации.
Для количественного описания этого закон фильтрации записывается в форме Дарси, но с переменной вязкости (эффективной):
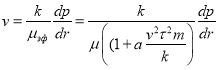 (1)
(1)
где ![]() — постоянная порядка десяти [].
— постоянная порядка десяти []. ![]() - скорость фильтрации,
- скорость фильтрации, ![]() -вязкость жидкости,
-вязкость жидкости, ![]() - время релаксации,
- время релаксации, ![]() — пористость,
— пористость, ![]() - проницаемость,
- проницаемость, ![]() - градиент давления. Последнее соотношения можно записать в виде
- градиент давления. Последнее соотношения можно записать в виде
![]() (2)
(2)
где
![]() ,
, ![]() (3)
(3)
С другой стороны, формулу (3) можно написать в виде:
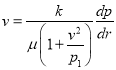 (4)
(4)
Обозначая ![]() , можно получить
, можно получить
![]() (5)
(5)
В формуле (2) подставляя ![]() , получаем
, получаем 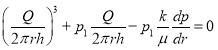 или
или
Интегрируя левую часть этого равенства от ![]() , до
, до ![]() , при
, при![]() получаем:
получаем:
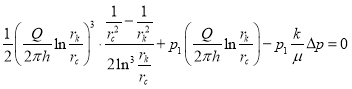 (7)
(7)
где ![]() - радиус призабойной зоны,
- радиус призабойной зоны, ![]() -радиус контура питания,
-радиус контура питания, ![]() - толщина пропластка,
- толщина пропластка, ![]() ,
, ![]() - давление призабойной зоне,
- давление призабойной зоне, ![]() - давление на контуре.
- давление на контуре.
Сделав подстановку
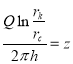 (8)
(8)
и разделив обе части равенства на 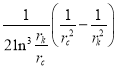 , мы получаем уравнение в виде:
, мы получаем уравнение в виде:
![]() (9)
(9)
где
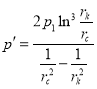 ,
, ![]() (10)
(10)
Формулу (8) можно записать в виде:
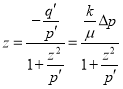 (11)
(11)
Если введем обозначения
![]() (12)
(12)
то получим из (10)
![]() (13)
(13)
Подставляя (8) и (12) в уравнение (13) получаем формулу
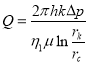 (14)
(14)
С другой стороны из формулы (12) получаются выражение
![]() (15)
(15)
или
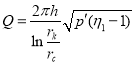 (16)
(16)
Так же сравнивая формулы (1) и (4) можно для времени релаксации получить формулу в виде:
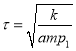 (17)
(17)
где ![]() находится из формулы (7)
находится из формулы (7)
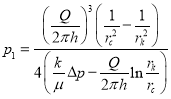 (18)
(18)
А теперь формулу (12) напишем в следующем виде:
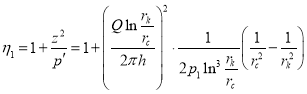
Так как ![]() то его можно отбросить. Тогда получаем
то его можно отбросить. Тогда получаем
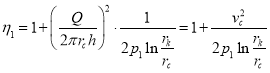
или
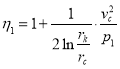 (19)
(19)
здесь ![]() - скорость фильтрации жидкости в при забойной зоне.
- скорость фильтрации жидкости в при забойной зоне.
Формулу можно также записать в виде:
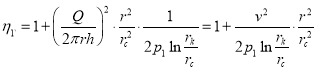 (20)
(20)
Используя (5) в (2) получаем
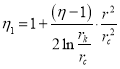 или
или
![]() (21)
(21)
При забойной зоне при![]() имеем:
имеем:
![]() (22)
(22)
Таким образом для определения эффективной вязкости поступаем следующим образом.
Сначала используя метод установившихся отборов строим зависимость ![]() . Тогда
. Тогда
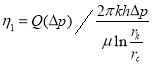 (23)
(23)
Так как ![]() то используя формулу (22) мы получаем расчетную формулу для определения эффективной вязкости.
то используя формулу (22) мы получаем расчетную формулу для определения эффективной вязкости.
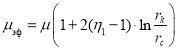 (24)
(24)
А теперь представим, что закон фильтрации имеет более общий вид:
![]() (25)
(25)
Для решения этого кубического уравнения используя подстановку ![]() получаем уравнение в виде:
получаем уравнение в виде:
![]() (26)
(26)
Здесь ![]() ,
, ![]() ,
, ![]()
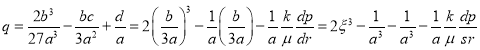 (27)
(27)
Формулу (26) можно представить в виде:
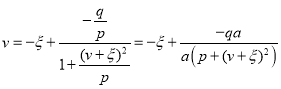 (28)
(28)
Следует отметить, что при ![]() получается предыдущая задача. Подставляя (27) в (28) мы получаем:
получается предыдущая задача. Подставляя (27) в (28) мы получаем:
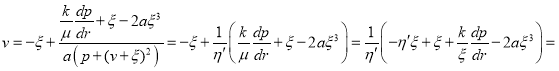
здесь ![]() ,
,
![]() (30)
(30)
Обозначая ![]() мы из (29) получаем
мы из (29) получаем
![]() (31)
(31)
Подставляя (27) в (30) мы получаем ![]() .
.
Таким образом
![]() (32)
(32)
В формуле (25) подставляя![]() получаем:
получаем:
![]() (33)
(33)
Интегрируя левую часть этого равенства от![]() до
до ![]() , а правую часть от
, а правую часть от ![]() до
до ![]() (при
(при ![]() ) получаем:
) получаем:
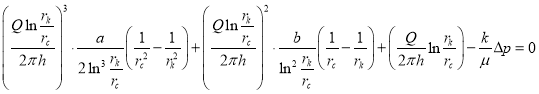 (34)
(34)
Сделав подстановку 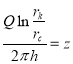 ,
, 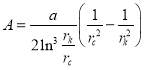 ,
, 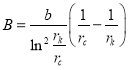 ,
,
![]() (35)
(35)
мы получаем кубическое уравнение в виде:
![]() (36)
(36)
Для решения этого уравнения так же используем подстановку ![]() ,
,
![]() . Тогда данное кубическое уравнение представится в виде:
. Тогда данное кубическое уравнение представится в виде:
![]() (37)
(37)
здесь ![]() ,
, ![]() ,
, 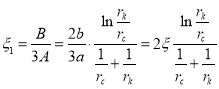 ,
,
![]() (38)
(38)
Уравнение (36) можно представить в виде:
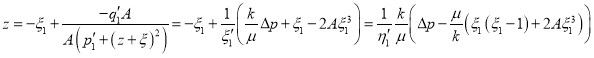 или
или
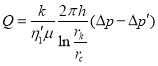 (39)
(39)
где ![]() ,
,
![]() (40)
(40)
Подставляя (38) в (40) получаем:
![]() (41)
(41)
Решая уравнение ![]() относительно
относительно
![]() (42)
(42)
Подставляя из (35) 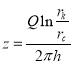 в (42) получаем
в (42) получаем
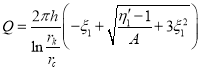 (43)
(43)
С другой стороны, решая уравнение (32) ![]() относительно
относительно ![]() получаем
получаем
Если решить уравнения (32) и (41) вместе, то получаем выражение
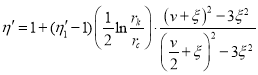 (45)
(45)
Если в (45) подставить ![]() , то получается формула (22), что и следовало ожидать. Следует так же отметить, что для определении времени релаксации можно использовать формулу (28). Тогда
, то получается формула (22), что и следовало ожидать. Следует так же отметить, что для определении времени релаксации можно использовать формулу (28). Тогда 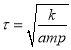 , (46), где по формуле (27)
, (46), где по формуле (27) ![]() . А теперь покажем, как можно найти
. А теперь покажем, как можно найти ![]() и
и ![]() в формуле (39).
в формуле (39).
По формуле (39) мы установили, что, 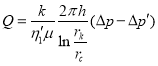
Преобразуем его в следующий вид
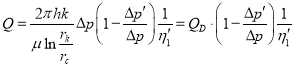 (48)
(48)
![]() (49)
(49)
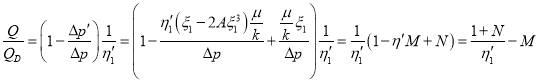 или
или
![]() (50)
(50)
где 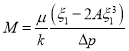 ,
, ![]() (51)
(51)
Следовательно, из (48), (49), (50), (51) мы получаем
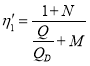 ,
,
![]() (52)
(52)
Для определения эффективной вязкости в случае, когда ![]() поступаем также, как и в случае
поступаем также, как и в случае ![]() . Строим зависимость
. Строим зависимость 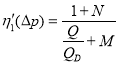 , где
, где 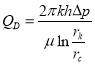 . Подставляя
. Подставляя ![]() и значение
и значение ![]() (
(![]() и
и ![]() можно получить из обработки исследования методом установившихся отборов) в (32) получаем
можно получить из обработки исследования методом установившихся отборов) в (32) получаем ![]() . Далее вычисляем
. Далее вычисляем
![]() (53)
(53)
А теперь покажем, как можно найти ![]() и а интерпретируя индикаторные линии скважин полученные при установившихся режимах фильтрации.
и а интерпретируя индикаторные линии скважин полученные при установившихся режимах фильтрации.
Для интерпретации индикаторных линий скважин при установившихся режимах фильтрации кубическое уравнение приведем в следующий вид:
![]() , (54)
, (54)
где 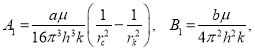 (55)
(55)
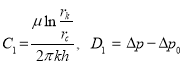
или ![]() (56)
(56)
Построим график зависимости ![]()
Как видно, графиком этой зависимости является парабола, которая пересекает ось ординат в точке, равной значению С1 (рис. 1). Откуда находим
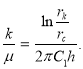 (57)
(57)
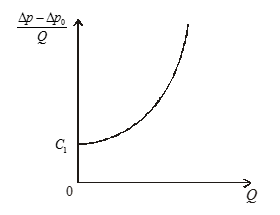
Рис. 1. График зависимости ![]() от Q
от Q
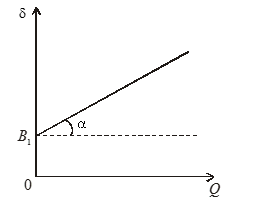
Рис. 2. График зависимости ![]() от Q.
от Q.
Если перестроим координаты и построим график зависимости  от Q, то получается прямая, которая пересекает ось ординат в точке, равной В1. Тангенс угла наклона этой прямой равен значению А1, т. е.
от Q, то получается прямая, которая пересекает ось ординат в точке, равной В1. Тангенс угла наклона этой прямой равен значению А1, т. е. ![]() (рис.2). Откуда для параметров а и b из (55) получаются зависимости для а и b
(рис.2). Откуда для параметров а и b из (55) получаются зависимости для а и b
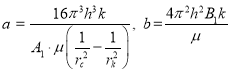 . (58)
. (58)
Эта задача актуальна, потому что увеличение градиента, направленное против движения, отрицательно влияет на количество извлекаемых запасов. Со временем актуальность этой задачи будет увеличиваться в связи с тем, что открываемые новые месторождения находятся на все более больших глубинах. А с увеличением глубины увеличивается и скорость, и градиент давления. Также необходимо иметь в виду, что в процессе длительной разработки имеет место трансформация легкоизвлекаемых запасов нефти в трудноизвлекаемые. Поэтому увеличиваются и сопротивления, связанные с влиянием инерционных сил.
Таким образом, в статье получены более общие формулы, учитывающие начальный градиент и влияние инерционных сил. В связи с этим их можно назвать соответственно обобщёнными формулами закона Дарси и Дюпюи. В работе также дана общая методика интерпретации соответствующих индикаторных линий.
Литература:
- А. Х. Мирзаджанзаде, О. Л. Кузнецов, К. С. Басниев, З. С. Алиев. Основа технологии добычи газа. — М.: Недра, 2003, 880 с.
- А. Х. Мирзаджанзаде, И. М. Аметов, А. Г. Ковалев. Физика нефтяного и газового пласта. — Москва-Ижевск: Институт компьютерных исследований, 2005. –280 с.
- А. Х. Мирзаджанзаде, А. Г. Ковалев, Ю. В. Зайцев. Особенности эксплуатации месторождений аномальных нефтей. –М.: Недра, 1972. – С.200.
- А. Т. Горбунов. Разработка аномальных месторождений. — М.: Недра, 1981. — 240 с.







