В статье предложены формулы для более простого определения скорости и дебита при двучленном законе фильтрации.
Получен аналитический вид формул для их определения, который в свою очередь позволяют количественно оценить влияние инерционных сил на скорость фильтрации и на дебит скважин.
Ключевые слова: градиент, давление, депрессия, фильтрация.
The article proposes formulas for a more simple determination of the rate and flow rate for a two-term filtering law.
An analytical form of the formulas for their determination is obtained, which in turn makes it possible to quantify the effect of inertial forces on the filtration rate and on well production.
Key words: gradient, pressure, depression, filtration.
При разработке залежей при больших градиентах давления на фильтрацию жидкости в пористой среде влияют инерционные силы, которые создают дополнительные сопротивления, направленные против движения. Таким образом, при больших скоростях течения природа нелинейности закона фильтрации иная, чем при малых скоростях фильтрации [1–3].
Как известно, при установившемся режиме двучленный закон фильтрации можно написать в следующем виде:
![]() (1)
(1)
Здесь
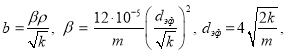
в котором значение b определяется по данным Е. М. Минского [4].
В выражении (2) ![]() – плотность жидкости, m — пористость породы, d — диаметр зерен, составляющий породу. Определение d, как правило, требует предварительного анализа исследуемой среды и довольно трудоемких экспериментов. В. Н. Щелкачев предложил в качестве линейного параметра d брать величину, пропорциональную корню квадратному из проницаемости.
– плотность жидкости, m — пористость породы, d — диаметр зерен, составляющий породу. Определение d, как правило, требует предварительного анализа исследуемой среды и довольно трудоемких экспериментов. В. Н. Щелкачев предложил в качестве линейного параметра d брать величину, пропорциональную корню квадратному из проницаемости.
В зависимости от скорости фильтрации значение b изменяется в широком диапазоне. С увеличением скорости значение в формуле (1) члена ![]() не только становится соизмеримо с членом
не только становится соизмеримо с членом ![]() но и становится намного больше. В связи с чем полученное значение скорости фильтрации оказывается меньше, чем по закону Дарси.
но и становится намного больше. В связи с чем полученное значение скорости фильтрации оказывается меньше, чем по закону Дарси.
После несложных преобразований уравнение (1) можно представить в виде:
![]()
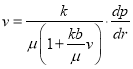 (2)
(2)
Как известно, с увеличением градиента давления увеличивается скорость и углеводороды не успевают пройти через поры, поэтому образуется дополнительное сопротивление.
Пусть ![]() и
и ![]() (3)
(3)
Тогда уравнение (2) представиться в виде:
![]() (4)
(4)
Для нахождения
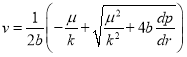 (5)
(5)
Из уравнений (4) и (5) можно получить
 (6)
(6)
Как известно, в уравнении (1) подставляя ![]() и интегрируя уравнение, взяв для
и интегрируя уравнение, взяв для ![]() пределы интегрирования от
пределы интегрирования от ![]() до
до ![]() для р от
для р от ![]() до
до ![]() , получим квадратное уравнение относительно
, получим квадратное уравнение относительно ![]() в следующем виде:
в следующем виде:
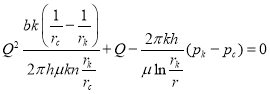 (7)
(7)
Это уравнение можно представить в виде:
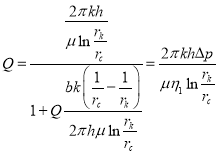 (8)
(8)
где
![]() ,
,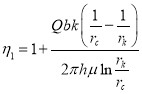 (9)
(9)
Так как ![]() то
то
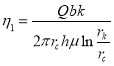 (10)
(10)
Учитывая, что ![]() то получаем
то получаем 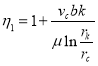 или
или
![]() (11)
(11)
Здесь ![]() .
.
С другой стороны, из (3) имеем
![]() (12)
(12)
Из (11) и (12) получаем
![]() (13)
(13)
С другой стороны
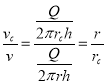 (14)
(14)
Приравнивая (13) и (14) получаем ![]() или
или
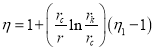 (15)
(15)
В призабойной зоне так как ![]() то
то
![]() (16)
(16)
Для получения ![]() и
и ![]() поступаем следующим образом. Решив квадратное уравнение относительно
поступаем следующим образом. Решив квадратное уравнение относительно ![]() получаем:
получаем:
 (17)
(17)
Тогда
 (18)
(18)
Проводя исследования методом установившихся отборов, можно найти зависимость ![]() . Далее, подставляя эту зависимость в (16), можно получить
. Далее, подставляя эту зависимость в (16), можно получить ![]() . Эту формулу можно сопоставить с формулой (12). Если исследования проведены правильно, то значения
. Эту формулу можно сопоставить с формулой (12). Если исследования проведены правильно, то значения ![]() , полученные по формулам (12) и (16), должны совпадать.
, полученные по формулам (12) и (16), должны совпадать.
Следует отметить, что при ![]() для нахождения скорости и дебита используются закон Дарси и формула Дюпюи.
для нахождения скорости и дебита используются закон Дарси и формула Дюпюи.
Следует также отметить, что правильно найденные значения ![]() и
и ![]() позволяют легко найти
позволяют легко найти ![]() и
и ![]() .
.
![]() и
и ![]() ,
, ![]() (19)
(19)
Мы видим, что последняя формула значительно проще, чем формула (17).
Литература:
- А. Х. Мирзаджанзаде, О. Л. Кузнецов, Х. С. Басниев, З. С. Алиев. Основа технологии добычи газа. — М.: Недра, 2003. –880 с.
- А. Х. Мирзаджанзаде, И. М. Аметов, А. Г. Ковалев. Физика нефтяного и газового пласта. –Москва-Ижевск: Институт компьютерных исследований. —2005. –280 с.
- К. С. Басниев, А. М. Власов, И. Н. Кочина, В. М. Максимов. Подземная гидравлика. –М.: Недра, 1986. — 303 с.
- Минский Е. М. О турбулентной фильтрации газа в пористых средах // Тр.ВНИИгаза. –М.: Гостоптехиздат, 1951. –С.64–71.







