Анализ зарубежной и отечественной теории и практики показывает, что наиболее предпочтительным для использования в системе управления развитием предприятия является показатель стоимости бизнеса, или стоимости предприятия. По мере развития рыночных отношений потребность в управлении стоимостью промышленных предприятий возрастает. Определение рыночной стоимости есть необходимое условие при приватизации, передаче в доверительное управление либо в аренду, продаже, национализации, выкупе. Определить стоимость организации также необходимо для выбора направления его реструктуризации. Процесс оценки стоимости предприятия включает выявление альтернативных подходов к управлению хозяйствующего субъекта и выбор того из них, обеспечивающий предприятию наибольшую эффективность, а, отсюда, и более высокую рыночную цену, что и выступает как основная цель собственников и главная задача топ-менеджеров организации.
Под управлением стоимостью предприятия понимается процесс целенаправленного воздействия со стороны топ-менеджеров и собственников предприятия на величину стоимости предприятия, которое осуществляется с целью максимизации ее величины. Реализация функции управления стоимостью предприятия в форме учета и контроля проходит через оценку стоимости организации. [6]
Основные цели и критерии успеха хозяйствующего субъекта, традиционно — это прибыль, рентабельность, доход. Получение дохода — это цель и конечный результат деятельности во многих отраслях экономики, т. е. цель и результат бизнеса. Вместе с этими показателями деятельности хозяйствующего субъекта выделяют такие показатели, как доля рынка, объем продаж, доля рынка относительно конкурента, доля отдельных товаров (услуг) в общем объеме продаж. Однако таким подходом для оценки деятельности компаний не дается адекватный ответ на вопрос успешна ли их деятельность. В связи с этим, перечень указанных и подобных им показателей подразумевает прямое использование данных бухгалтерского учета, которыми может скрываться реальное положение. Помимо этого, в роли недостатков выступает и то, что традиционные показатели игнорируют временную стоимость денег, что является очень актуальным, когда рассматривается долгосрочный период.
В связи со сменой парадигмы управления, выдвижением вперед стратегического подхода происходит диктование и новых принципов оценки успешности деятельности предприятия. В научной литературе называются разные отличительные черты стратегического и тактического подходов к управлению. [1] Обычно считается, что главное отличие тактического от стратегического подхода заключается во временной составляющей: стратегическое — долгосрочное, тактическое — краткосрочное планирование. Краткосрочными целями определяется отражение те непосредственных результатов, которых руководство намерено получить в ближайшее время. Долгосрочными целями определяется, что необходимо делать сейчас, чтобы предприятием занималось такое положение, позволяющее ему эффективно работать в течение длительного времени.
Показатель стоимости предприятия, во-первых, носит комплексный характер (его значение определяется воздействием большого числа как внутренних факторов, характеризующих имеющиеся у предприятия ресурсы и эффективность их использования, так и внешних, отражающих отношение к предприятию со стороны потребителей и акционеров), а во-вторых, в отличие от наиболее распространенного оценочного показателя — прибыли — он достаточно тесно связан с ожидаемой перспективой развития предприятия (любое предположение о замедлении темпов роста достаточно быстро приводит к снижению показателя стоимости предприятия).
Таким образом, стоимость проявляется как ключевой момент системы стратегического управления развитием предприятия и используется как при формировании конкретных целей и задач, так и в роли критерия для оценки успешности реализации той или иной стратегии. [3]
Сущность оценки эффективности управления развитием заключается в изучении возможности применения математических методов и моделей, а именно корреляционно-регрессионного анализа, в оценке бизнеса, а также разработка моделей зависимости стоимости компании от ряда показателей ее хозяйственной деятельности. [7]
Для целей дальнейшего исследования возьмем данные промышленного предприятия ООО «Стойторг». В качестве результативной переменной возьмем величину стоимости оцениваемой компании. Регрессионную модель построим, проанализировав зависимость рыночной стоимости от различных ценообразующих показателей деятельности компаний. В качестве таких показателей выступили опыт руководителя в годах, величина чистой прибыли и активы предприятия.
Имеются данные по предприятию ООО «Стройторг» за 2011–2017 гг.:
1) Стоимость компании (трлн. руб.) — (
2) Опыт руководителя (в гг.) — ![]() )
)
3) Величина чистой прибыли (млрд руб.) — (![]() ).
).
4) Активы предприятия (трлн руб.)
Для характеристики зависимости рыночной стоимости компании от опыта руководителя, величины чистой прибыли и суммы активов, то есть ![]() от
от ![]() ,
, ![]() и
и ![]() выполним следующие пункты: [2]
выполним следующие пункты: [2]
1) Рассчитать параметры линейной функции.
2) Определить теоретическое уравнение множественной регрессии.
3) Найти коэффициенты парной корреляции.
4) Провести проверку значимости уравнения множественной регрессии с помощью F критерия Фишера.
5) Оценить статистическую значимость коэффициента множественной корреляции и детерминации.
6) Оценить модель через среднюю ошибку аппроксимации.
Таблица 1
|
Период |
Стоимость компании, трлн руб. |
Опыт руководителя,гг. |
Чистая прибыль, млрд руб. |
Активы, трлн руб. |
|
2011 |
1,2418 |
30 |
392,10 |
1,8608 |
|
2012 |
1,7970 |
31 |
377,66 |
2,3222 |
|
2013 |
2,0498 |
32 |
346,62 |
2,5072 |
|
2014 |
2,1760 |
33 |
126,21 |
2,7296 |
|
2015 |
2,4049 |
34 |
228,89 |
3,3556 |
|
2016 |
5,2621 |
35 |
322,98 |
6,2597 |
|
2017 |
5,9347 |
36 |
797,82 |
6,4350 |
Уравнение множественной регрессии.
Для оценки параметров уравнения множественной регрессии применяют метод наименьших квадратов (МНК).
Определим вектор оценок коэффициентов регрессии. Согласно методу наименьших квадратов, вектор s получается из выражения: s = (XTX)-1XTY.
К матрице с переменными Xj добавляем единичный столбец:
|
Х1 |
Х2 |
Х3 |
|
|
1 |
30 |
392.1 |
1.8608 |
|
1 |
31 |
377.66 |
2.3222 |
|
1 |
32 |
346.62 |
2.5072 |
|
1 |
33 |
126.21 |
2.7296 |
|
1 |
34 |
228.89 |
3.3556 |
|
1 |
35 |
322.98 |
6.2597 |
|
1 |
36 |
797.82 |
6.435 |
Матрица Y:
|
Y |
|
1.2418 |
|
1.797 |
|
2.0498 |
|
2.176 |
|
2.4049 |
|
5.2621 |
|
5.9347 |
Матрица XT:
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
30 |
31 |
32 |
33 |
34 |
35 |
36 |
|
392.1 |
377.66 |
346.62 |
126.21 |
228.89 |
322.98 |
797.82 |
|
1.8608 |
2.3222 |
2.5072 |
2.7296 |
3.3556 |
6.2597 |
6.435 |
Умножаем матрицы, (XTX):
|
7 |
231 |
2592.28 |
25.4701 |
|
231 |
7651 |
86535.31 |
862.9593 |
|
2592.28 |
86535.31 |
1225667.339 |
10743.963 |
|
25.4701 |
862.9593 |
10743.963 |
114.445 |
В матрице, (XTX) число 7, лежащее на пересечении 1-й строки и 1-го столбца, получено как сумма произведений элементов 1-й строки матрицы XT и 1-го столбца матрицы X.
Умножаем матрицы, (XTY):
|
20.8663 |
|
709.9519 |
|
9135.532 |
|
96.7614 |
Находим обратную матрицу (XTX)-1:
|
(XT X) -1 = |
211 |
-7,113 |
-0,0146 |
8,048 |
|
-7,113 |
0,241 |
0,000467 |
-0,276 |
|
|
-0,0146 |
0,000467 |
6,0E-6 |
-0,00086 |
|
|
8,048 |
-0,276 |
-0,00086 |
0,383 |
Вектор оценок коэффициентов регрессии равен:
|
Y(X) = |
211 |
-7,113 |
-0,0146 |
8,048 |
* |
20,866 |
= |
-1,875 |
|
-7,113 |
0,241 |
0,000467 |
-0,276 |
709,952 |
0,0423 |
|||
|
-0,0146 |
0,000467 |
6,0E-6 |
-0,00086 |
9135,532 |
0,000853 |
|||
|
8,048 |
-0,276 |
-0,00086 |
0,383 |
96,761 |
0,859 |
Отсюда, уравнение регрессии (оценка уравнения регрессии) представится следующим образом:
![]()
Найдем парные коэффициенты корреляции по следующей формуле:
![]()
![]()
Т. к. парный коэффициент корреляции ![]() , то связь между y и x1 сильная.
, то связь между y и x1 сильная.
![]()
Т. к. парный коэффициент корреляции ![]() , то связь между y и x2 умеренная.
, то связь между y и x2 умеренная.
Т. к. парный коэффициент корреляции ![]() , то связь между y и x3 сильная.
, то связь между y и x3 сильная.
|
Признаки x и y |
∑xi |
|
∑yi |
|
∑xiyi |
|
|
Для y и x1 |
231 |
33 |
20.866 |
2.981 |
709.952 |
101.422 |
|
Для y и x2 |
2592.28 |
370.326 |
20.866 |
2.981 |
9135.532 |
1305.076 |
|
Для y и x3 |
25.47 |
3.639 |
20.866 |
2.981 |
96.761 |
13.823 |
|
Для x1 и x2 |
2592.28 |
370.326 |
231 |
33 |
86535.31 |
12362.187 |
|
Для x1 и x3 |
25.47 |
3.639 |
231 |
33 |
862.959 |
123.28 |
|
Для x2 и x3 |
25.47 |
3.639 |
2592.28 |
370.326 |
10743.963 |
1534.852 |
Дисперсии и среднеквадратические отклонения.
|
Признаки x и y |
|
|
|
|
|
Для y и x1 |
4 |
2.886 |
2 |
1.699 |
|
Для y и x2 |
37954.199 |
2.886 |
194.818 |
1.699 |
|
Для y и x3 |
3.11 |
2.886 |
1.764 |
1.699 |
|
Для x1 и x2 |
37954.199 |
4 |
194.818 |
2 |
|
Для x1 и x3 |
3.11 |
4 |
1.764 |
2 |
|
Для x2 и x3 |
3.11 |
37954.199 |
1.764 |
194.818 |
Матрица парных коэффициентов корреляции R:
|
- |
y |
x1 |
x2 |
x3 |
|
y |
1 |
0.8983 |
0.6078 |
0.9936 |
|
x1 |
0.8983 |
1 |
0.363 |
0.9091 |
|
x2 |
0.6078 |
0.363 |
1 |
0.5454 |
|
x3 |
0.9936 |
0.9091 |
0.5454 |
1 |
Анализ параметров уравнения регрессии.
Проведем статистический анализ полученного нами уравнения регрессии: проверку значимости уравнения и его коэффициентов, исследование средней ошибки аппроксимации. [4]
Несмещенная ошибка ε = Y — Y(x) = Y — X*s (абсолютная ошибка аппроксимации)
|
Y |
Y(x) |
ε = Y — Y(x) |
ε2 |
(Y-Yср)2 |
|ε: Y| |
|
1.242 |
1.327 |
-0.0856 |
0.00733 |
3.024 |
0.0689 |
|
1.797 |
1.754 |
0.0431 |
0.00186 |
1.402 |
0.024 |
|
2.05 |
1.929 |
0.121 |
0.0147 |
0.867 |
0.0591 |
|
2.176 |
1.974 |
0.202 |
0.0408 |
0.648 |
0.0928 |
|
2.405 |
2.642 |
-0.237 |
0.0562 |
0.332 |
0.0986 |
|
5.262 |
5.26 |
0.00187 |
3.0E-6 |
5.204 |
0.000355 |
|
5.935 |
5.858 |
0.0765 |
0.00586 |
8.725 |
0.0129 |
|
0.127 |
20.201 |
0.357 |
Отсюда, средняя ошибка аппроксимации равна:
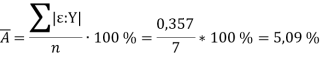
Поскольку ошибка аппроксимации не превышает 8–10 %, то данная модель адекватна и применима для анализа.
Множественный коэффициент корреляции.
Тесноту совместного влияния факторов на результат оценивает коэффициент множественной корреляции:
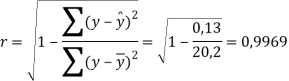
Поскольку коэффициент корреляции равен 0,997, значит, совместное влияние ![]() и
и ![]() на
на ![]() сильное.
сильное.
Найдем квадрат множественного коэффициента корреляции — коэффициент детерминации, который чаще всего выражают в процентах. [5]
Коэффициент детерминации равен:
R2= 0.99692 = 0.9937
Чем ближе этот коэффициент к единице, тем больше уравнение регрессии объясняет поведение Y. В нашем случае, мы видим, что в 99,4 % случаев изменения ![]() ,
, ![]() и
и ![]() влекут за собой изменение
влекут за собой изменение ![]() . Иначе говоря- точность подбора уравнения регрессии — высокая. Прочие 0,6 % изменения
. Иначе говоря- точность подбора уравнения регрессии — высокая. Прочие 0,6 % изменения ![]() объясняются факторами, которые не учтены в модели.
объясняются факторами, которые не учтены в модели.
Проверка общего качества уравнения множественной регрессии.
Проведем проверку значимости уравнения множественной регрессии по ![]() распределению Фишера.
распределению Фишера.
Табличное значение критерия со степенями свободы ![]() и
и ![]()
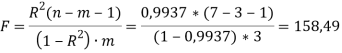
Поскольку ![]() , т. е.
, т. е. ![]() , принимается гипотеза о значимости уравнения регрессии и статистически надежно.
, принимается гипотеза о значимости уравнения регрессии и статистически надежно.
Таким образом, для оценки эффективности развитием предприятия для ООО «Стройторг» была изучена зависимость стоимости компании от ценообразующих факторов: опыта руководителя, величины чистой прибыли и активов предприятия.
В результате проведенных нами расчетов по предприятию ООО «Стройторг» было получено следующее уравнение множественной регрессии:
Y = -1.8749 + 0.04229X1 + 0.000853X2 + 0.8594X3.
Отсюда, можно представить экономическую интерпретацию параметров модели:
– увеличение опыта руководителя (X1) на 1 единицу измерения приводит к увеличению величины стоимости предприятия (Y) в среднем на 0.0423 единиц измерения;
– увеличение чистой прибыли (X2) на 1 единицу измерения приводит к увеличению величины стоимости предприятия (Y) в среднем на 0.000853 единиц измерения;
– увеличение активов предприятия (X3) на 1 единицу измерения приводит к увеличению величины стоимости предприятия (Y) в среднем на 0.859 единиц измерения.
Статистическая значимость и надежность уравнения проверена с помощью коэффициента детерминации и критерия Фишера.
Установлено, что в исследуемой ситуации 99.37 % общей вариабельности Y объясняется изменением факторов Xj. Установлено также, что параметры модели статистически значимы.
Поскольку ошибка аппроксимации
Литература:
- Богатко А. Н. Система управления развитием предприятия. — М.: Финансы и статистика, 2013. –240 с.
- Карев, В. П. Математическое моделирование бизнеса. Оценка, инвестиционное проектирование, управление предприятием. — М.: «Маросейка», 2010.- 168с.
- Кечеджиян Марина. Разработка стратегии развития производственного предприятия. — М.: LAP Lambert Academic Publishing, 2012. — 826 c.
- Кубланов М. С. Математическое моделирование. Методология и методы разработки математических моделей механических систем и процессов. Часть I. Моделирование систем и процессов. Издание третье, переработанное и дополненное: Учебное пособие.– М.: МГТУ ГА, 2004. — 108 с.
- Кузнецов В. Л. Математическое моделирование: Учебное пособие.- М.: МГТУГА, 2003. — 78 с.
- Спиридонова Е. А. Оценка стоимости бизнеса. Учебник и практикум для бакалавриата и магистратуры. — Гриф УМО ВО, 2018. — 299 с.
- Щербаков В. А., Щербакова Н. А. Оценка стоимости предприятия (бизнеса) — «Омега-Л», 2012, — 288 с.







