В данной статье представлен фрагмент дополнительного занятия по математике по теме «Принцип Дирихле» в 6 классе. Рассматриваются различные формулировки принципа Дирихле, а также приводятся примеры применения принципа Дирихле при решении геометрических задач.
Ключевые слова: геометрические задачи, концепции математического образования, дополнительное математическое образование (ДМО), математический кружок, принцип Дирихле.
Согласно Концепции математического образования значительную роль играет воспитательная составляющая деятельности школы. В наше время, как установлено, креативный подход приобретает наиболее пристальное внимание изучающего интереса, так как общество нуждается в массовом совершенствование ранее известного, в отказе от устойчивых и привычных, но пришедших в противоречие с имеющимися потребностями и возможностями форм. А это в свою очередь значит возрастание роли внеурочной деятельности. Проделанная работа П. М. Гурева и его собственная практика обучение школьников математике в ДМО обосновала то, что важные формой организации работы в дополнительном математическом образовании являются занятия математического кружка [2].
Вопросы, которые решают на занятиях математического кружка, выходят за пределы объема обязательных заданий, но они взаимосвязаны с основными вопросами программного материала в данном классе. В данной статье предлагается создание дополнительного занятия по математике в шестом классе на рассмотрение «Принципа Дирихле».
Рассмотрение принципа Дирихле на дополнительном задании преследует следующие цели:
Объяснить учащимся новый математический метод решения задачи, не рассматриваемый в школьной программе, научить на конкретных примерах применение данного принципа при решении геометрических задач.
Принцип Дирихле выражает отношение между двумя множествами. Есть много формулировок этого принципа.
Применяя данный принцип для решение определенной задачи, нужно разобраться, что будем выражать за «клетки», а что за «зайцев».
Одна из самых распространённых формулировок принципа Дирихле трактуется так: «Если в n клеток посадить n+1 зайцев, то найдется хотя бы одна клетка, в которой находится не менее чем 2 зайца» [1].
Обобщенный принцип Дирихле: «Если в n клеток посадить kn+1 зайцев, то найдётся хотя бы одна клетка, в которой находятся не менее чем k+1 заяц».
Рассмотрим геометрические задачи, которые опираются на дискретный принцип Дирихле.
Задача № 1. В равносторонний треугольник со стороной равной 2 см поместили 5 точек. Докажите, что найдутся такие две точки, расстояние между которыми меньше 1 см.
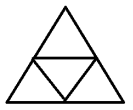
Рис. 1
Решение.
Нарисуем чертеж. Разделим наш треугольник на 4 равных треугольника (рис. 1). Стороны новых треугольников будут равны 1 см. Так как помещают 5 точек, то в один из полученных треугольников попадет хотя бы 2 точки, расстояние между которыми будет меньше стороны треугольника, т. е. меньше 1 см.
Задача № 2. Докажите, что если прямая M, расположенная в плоскости треугольника ABC, не проходит ни через одну из его вершин, то она не может пересечь все три стороны треугольника [3].
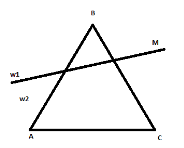
Рис. 2
Решение. Полуплоскости, на которые прямая M разбивает плоскость треугольника ABC, обозначим через
Пусть, точки A и B находятся в одной полуплоскости, то есть лежат по одну сторону от прямой M. Тогда отрезок AB не пересекается с М. Итак, в треугольнике ABC нашлась сторона, которая не пересекается с прямой M.
При изучении «Принципа Дирихле» на дополнительном занятии выделим следующие:
Принцип Дирихле является эффективным методом решения задач. Но для его применения на первых этапах изучения темы надо научиться определять какой объекты считать зайцем, а какой клеткой, при этом следить за тем, чтобы зайцев всегда было больше, чем клеток. А затем научиться пользоваться фактом наличия в одной клетке двух зайцев, и делать необходимые выводы.
Литература:
- Андреев, А. А. Принцип Дирихле: учеб. для вузов / Г. Н. Горелов, А. Н. Люлев. — Самара: Пифагор, 2016. — 84 с.
- Горелов, П. М. Система внеклассной работы по математике в средней школе № 21 города Кирова / П. М. Горелов. — Киров: ВСЭИ, 2014. — 233 с.
- Летчиков, А. В. Принцип Дирихле. Задачи с указаниями и решениями: Учебное пособие / А. В. Летчиков. — Ижевск: Издательство Удм. ун-та, 2015. — 108 с.







