If concerning initial investments the investor has enough exact information it is impossible to tell concerning other streams. These streams are connected with many неопределенностями concerning the future condition of the market, economy as a whole etc. In many cases these of uncertainty appear ineradicable and involve ineradicable risks of the made decision. Therefore struggle against risk and management of it is the primary goal of the investor, both at a working out stage, and at a stage of realization of the project.
Keywords: the investment project, management of risk, risk estimation.
Ключевые слова: инвестиционный проект, управление риском, оценка риска.
Введение. Известно, что каждый инвестиционный проект предполагает планирование и управление в основном трёх денежных потоков:
а) инвестиционный поток;
б) текущий поток (текущие расходы);
в) входящий поток (прибыли).
Если относительно начальных инвестиций инвестор располагает довольно точной информацией, то этого нельзя сказать относительно других потоков. Эти потоки связаны со многими неопределенностями, относительно будущего состояния рынка, экономики в целом и т.д. Во многих случаях эти неопределённости оказываются неустранимыми и влекут за собой неустранимые риски принятого решения. Поэтому борьба с риском и управление им является основной задачей инвестора, как на стадии разработки, так и на стадии реализации проекта.
С другой стороны, борьба и управление риском проходит через его количественную оценку.
Успешное управление риском зависит от того в какой степени количественная оценка риска оказывается адекватной к реальной жизни.
В финансовом анализе существуют, в основном три направления для оценки риска:
а) вероятностно-статистические методы;
б) минимально-максимальные методы;
в) нечёткомножественные методы.
Не обсуждая преимущества и недостатки этих подходов (см. для этого [1]) отметим, что мы будем рассматривать случае, когда параметры инвестиционного проекта заданы как нечёткие треугольные числа.
Постановка задачи. Предложим, что некоторого показателя инвестиционного проекта 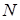 (например,
(например, 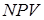 ) при условии, что
) при условии, что 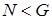 проект считается неэффективным.
проект считается неэффективным.
Предложим, что множества возможных значений показателя 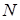 и критерия
и критерия 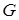 заданы как треугольные нечётные числа
заданы как треугольные нечётные числа
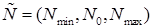 ,
, 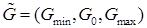 . Требуется используя заданные параметры нечётких чисел
. Требуется используя заданные параметры нечётких чисел 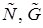 оценить риск заданного проекта.
оценить риск заданного проекта.
Решение задачи. Функция принадлежностей заданных треугольных чисел имеют вид:
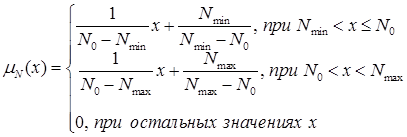
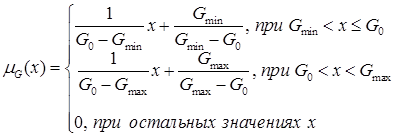
соответственно. Если начертить графики функций 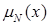
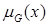 на одной координатной плоскости, то в зависимости от значений
на одной координатной плоскости, то в зависимости от значений 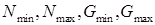 возможны различные расположения этих графиков относительно друг друга. Общая схема рассуждений используемых в данной работе не зависит от расположения треугольных числе
возможны различные расположения этих графиков относительно друг друга. Общая схема рассуждений используемых в данной работе не зависит от расположения треугольных числе 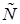 и
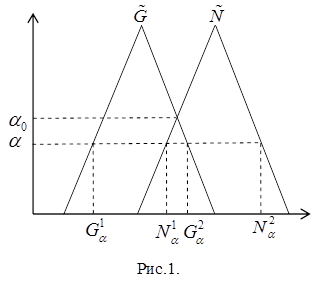
и 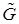 , и поэтому, мы будем рассматривать один из вариантов, показанный на рис.1 более подробно.
, и поэтому, мы будем рассматривать один из вариантов, показанный на рис.1 более подробно.
Следуя [2] рассмотрим 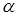 - уровневые множества нечётных чисел
- уровневые множества нечётных чисел 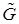 и
и 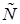 . Будем считать, что условие
. Будем считать, что условие 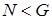 в
в 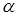 - уровневых множествах порождает риск неэффективности реализации инвестиционного проекта.
- уровневых множествах порождает риск неэффективности реализации инвестиционного проекта.
При 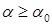 (см.рис.1) соответствующие
(см.рис.1) соответствующие 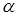 - уровневые интервалы не пересекаются и следовательно, рисковая зона отсутствует, а при
- уровневые интервалы не пересекаются и следовательно, рисковая зона отсутствует, а при 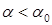 опасность того, что значения
опасность того, что значения 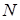 , входящие в пересечение интервалов.
, входящие в пересечение интервалов. 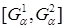 и
и 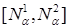 могут быть меньше, чем значения
могут быть меньше, чем значения 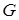 , то есть интервал
, то есть интервал 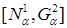 является рискованной зоной.
является рискованной зоной.
Перенося для выбранного 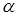 соответствующие интервалы на
соответствующие интервалы на 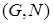 - плоскость получаем следующую картину (рис.2).
- плоскость получаем следующую картину (рис.2).
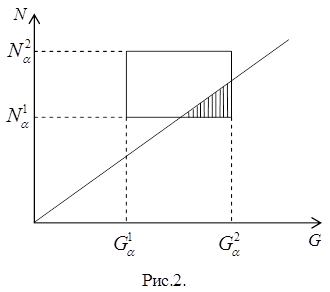
Здесь заштрихованная часть рисунка показывают зону риска, а весь прямоугольник - область всевозможных реализаций проекта.
Для выбранного 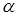 - уровня вероятности попадания точки
- уровня вероятности попадания точки 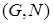 в заштрихованную область есть вероятность неэффективности проекта для этой пары значений параметров.
в заштрихованную область есть вероятность неэффективности проекта для этой пары значений параметров.
Обозначим через 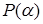 эту вероятность. Тогда
эту вероятность. Тогда 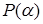 определится по формуле:
определится по формуле:
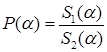
где 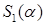 - площадь заштрихованной области,
- площадь заштрихованной области, 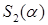 - площадь прямоугольной области.
- площадь прямоугольной области.
После того, как мы определили вероятности для всех 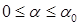 , можно оценить риск неэффективности реализации инвестиционного проекта с помощью этих вероятностей.
, можно оценить риск неэффективности реализации инвестиционного проекта с помощью этих вероятностей.
Прежде, чем перейти к оценке риска, отметим некоторые свойства функции 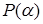 .
.
1. Если выразить площади 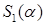 ,
, 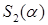 , через
, через 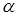 в явном виде, то после элементарных преобразований получим:
в явном виде, то после элементарных преобразований получим:
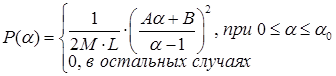
где 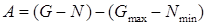 ,
, 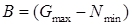 ,
, 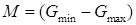 ,
,
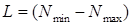
2. 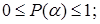
3. 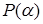 - убывающая на отрезке
- убывающая на отрезке 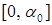 функция;
функция;
4. 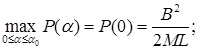
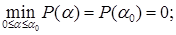
5. 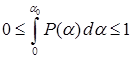 .
.
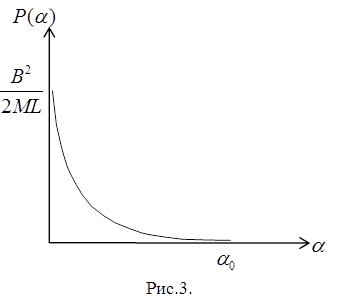
График этой функции показан на рис.3.
Оценка риска может осуществляется на основе различных подходов. рассмотрим некоторые из них.
Первый подход заключается в том, что в качестве оценки риска неэффективности реализации инвестиционного проекта берётся площадь области ограниченной кривой функции 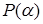 (рис.3) и координатными осями.
(рис.3) и координатными осями.
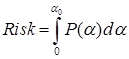 (1)
(1)
Такой подход достаточно обстоятельно рассмотрен в [2] и мы не будем приводить его здесь.
Во втором подходе, предлагаемом нами, в качестве оценке риска, соответствующему 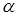 -уровню, берётся значение вероятности
-уровню, берётся значение вероятности 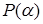 . Таким образом, для каждого
. Таким образом, для каждого 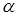 имеется свой риск. Однако, риск для отдельного
имеется свой риск. Однако, риск для отдельного 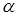 не может характеризовать весь проект в целом, так как
не может характеризовать весь проект в целом, так как 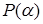 носит в некотором смысле локальный характер. Поэтому здесь уместно ввести величину максимального риска, то есть в качестве оценки риска всего проекта предлагается взять максимальное значение вероятности
носит в некотором смысле локальный характер. Поэтому здесь уместно ввести величину максимального риска, то есть в качестве оценки риска всего проекта предлагается взять максимальное значение вероятности 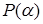 :
:
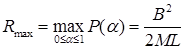 (2)
(2)
Отметим некоторые преимущества формулы (2) над формулой (1).
1) Максимальный риск не зависит от значений 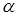 . Он только зависит от значений
. Он только зависит от значений 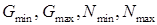 . Это значит, что при определении рисковой зоны (рис.2) нужно взять
. Это значит, что при определении рисковой зоны (рис.2) нужно взять 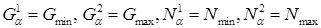 .
.
2) Сравнение формул (1) и (2) показывает, что оценка по формуле (2) оказывается искусственно завышенной, по сравнению с формулой (1). Другими словами, значение риска, вычисленное по формуле (2) больше, чем его реальное значение.
3) Оценка риска по формуле (2) даёт возможность оценить риск, в случае необходимости, лингвистически. Такая оценка может производиться с помощью различных шкал и уровней. При этом используются только величины 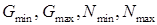 .
.
Например, в рассмотренном нами простом случае, если 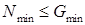 максимальный риск
максимальный риск
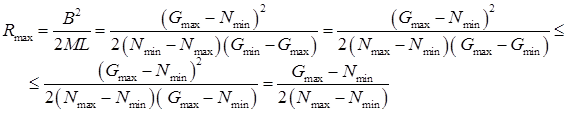
здесь мы воспользовались тем, что 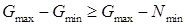 .
.
Соотношение (3) может быть использовано для классификации риска. К примеру, если 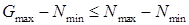 , то
, то 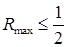 , что означает риск, находится между 0% и 50%.
, что означает риск, находится между 0% и 50%.
Лингвистическая оценка риска оказывается полезным, когда рассматриваемая задача является составной частью задач более высокого уровня, которые исследуются лингвистическими методами.
Заметим, что оценка риска по формуле (1) создают определенные трудности в оценке риска в зависимости от соотношений между параметрами нечётких чисел 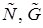 . В этом случае, чтобы классифицировать риск может быть использован только значения
. В этом случае, чтобы классифицировать риск может быть использован только значения 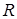 из формулы (1).
из формулы (1).
Литература:
1. Недосекин А.О. Финансовый менеджмент в условиях неопределенности: Вероятности или чёткие множества? SPb Ru/analytic/vm/Public5.htm
2. Недосекин А.О. Методологические основы моделирования финансовой деятельности с использованием нечёткомножественных описаний. Санкт-Петербург. 2003, 323 с.







