Общеизвестно, что для чистого среза стеблей необходимо, чтобы они не скользили по лезвию к меньшему основанию сегмента в процессе подвода стеблей к противорежущей пластине [1].
Боковые стороны сегмента наклонены к оси его симметрии под углом α (рисунок 1). В процессе среза стеблей скорость абсолютного движения любой точки сегмента (VАБ) переменна как по численному значению, так и по направлению. В зависимости от ее направления угол защемления стебля в режущей паре (δ) между линией вектора скорости сегмента (VАБ) и линией режущей кромки сегмента (линия ma), может быть как меньше 90º (рисунок 1 а), так и больше 90º (рисунок 1 б) [1].
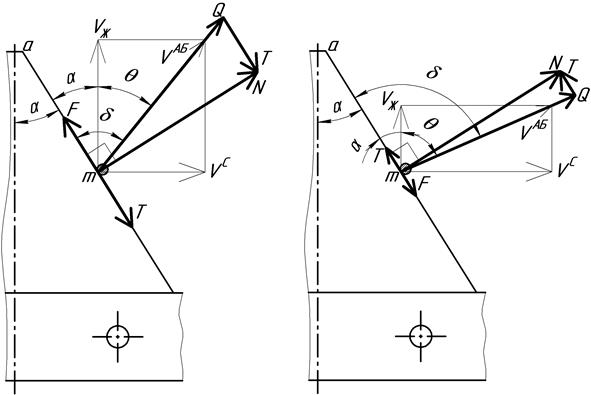
а б
а, б – с возможным проскальзыванием стебля к нижнему или верхнему основанию сегмента соответственно
Рисунок 1. – Схема действия сил сегмента на стебель в процессе подвода к линии резания
Математически два этих условия можно записать в виде следующих неравенств [1]
|
δ = α + θ < 90º, |
(1) |
|
δ = α + θ > 90º, |
(2) |
где δ – угол защемления стебля в режущей паре, град.;
α – угол наклона режущей кромки сегмента к оси его симметрии, град.;
θ – угол между вектором скорости жатвенного агрегата (VЖ) и вектором абсолютной скорости сегмента (VАБ), град.
Если угол защемления стебля в режущей паре (δ) менее 90º (неравенство (1)), то вектор силы трения (Т) направлен к нижнему основанию сегмента, если же угол защемления стебля в режущей паре (δ) более 90º (неравенство (2)), то вектор силы трения (Т) направлен к верхнему основанию сегмента. В первом случае не наблюдается выскальзывание стеблей из раствора режущих кромок сегментов при срезе. Во втором случае будет наблюдаться выскальзывание стеблей из раствора режущих кромок сегментов.
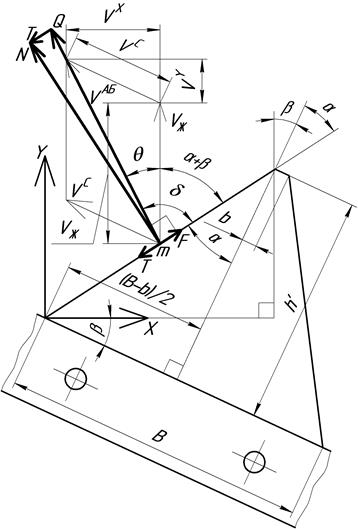
Рисунок 2. – Схема определения условия защемления стебля между сегментами режущего аппарата, развернутого на угол β относительно направления движения жатвенного агрегата при движении сегмента справа налево
В конструкции прицепной жатки-накопителя с прямоугольной формой платформы [2] режущий аппарат расположен под углом β относительно направления движения жатвенного агрегата. Определим при таком расположении режущего аппарата условие защемления стебля в режущей паре.
В случае, когда сегмент ножа движется справа налево (рисунок 2) и вектор силы трения (Т), проведенный из конца вектора результирующей силы (Q) в конец вектора силы нормальной реакции (N), направлен к нижнему основанию сегмента, обеспечивается выполнение условия защемления стебля.
Математически условие защемления стебля в режущей паре, как видно из схемы, приведенной на рисунке 2, будет описано следующим неравенством
|
δ = α + β + θ < 90º, |
(3) |
где β – угол поворота режущего аппарата относительно направления движения жатвенного агрегата, град.
Из представленной на рисунке 2 схемы видно, что угол (θ) между вектором скорости жатвенного агрегата (VЖ) и вектором абсолютной скорости сегмента (VАБ) определиться по выражению
|
θ = arc tan (VX / (VЖ + VY)), |
(4) |
где VX и VY – проекция вектора относительной скорости сегмента (VC) на оси Х и Y (ось Y направлена параллельно вектору движения жатвенного агрегата, ось Х направлена перпендикулярно оси Y), как видно из схемы, представленной на рисунке 2, данные составляющие выражения (4) определятся по следующим формулам
|
VX = VC cos β, |
(5) |
|
VY = VC sin β, |
(6) |
где VC – вектор относительной скорости сегмента, м/с;
VЖ – вектор скорости движения жатвенного агрегата.
Анализируя выражения (4), (5) и (6) можно прийти к следующему выводу. Величина угла θ зависит от значения скорости движения жатвенного агрегата (VЖ), значения относительной скорости сегмента ножа (VC) и величины угла поворота режущего аппарата (β) прицепной жатки накопителя с прямоугольной формой платформы.
Угол наклона режущей кромки сегмента к оси его симметрии (α), исходя из схемы представленной на рисунке 2, можно определить по следующему выражению
|
α = arc tan (((B – b) / 2) / h′), |
(7) |
где B и b – ширина нижнего и верхнего оснований сегмента соответственно; м;
h′ – высота режущей части сегмента, м.
Из выражения (7) видно, что угол наклона режущей кромки сегмента к оси его симметрии (α) при постоянном значении высоты режущей части сегмента (h′) может изменяться в зависимости от значений величин нижнего и верхнего оснований сегмента (В и b).
После всех преобразований составляющих неравенства (3) с учетом выражений (4)…(7) условие защемления стеблей в режущей паре при движении сегмента справа налево можно представить в виде следующего неравенства
|
δ = arc tan (((B – b) / 2) / h′) + β + + arc tan (VC ∙ cos β / (VЖ + VC ∙ sin β)) < 90º. |
(8) |
Далее рассмотрим случай, когда сегмент ножа движется слева направо (рисунок 3) и вектор силы трения (Т), проведенный из конца вектора результирующей силы (Q) в конец вектора силы нормальной реакции (N), направлен к нижнему основанию сегмента, при этом обеспечивается выполнение условия защемления стебля.
Из схемы, приведенной на рисунке 3 видно, что математически условие защемления стебля в режущей паре будет описано следующим неравенством
|
δ = α – β + θ < 90º. |
(9) |
Угол α определится также по выражению (7)
При рассмотрении схемы, представленной на рисунке 3 видно, что угол (θ) между вектором скорости жатвенного агрегата (VЖ) и вектором абсолютной скорости сегмента (VАБ) определится из следующего выражения
|
θ = arc tan (VX / (VЖ – VY)). |
(10) |
Проекции вектора относительной скорости сегмента (VC) на оси Х (VX) и Y (VY) определяться также по выражениям (5) и (6).
После всех преобразований неравенства (9) с учетом выражений (5)…(7) и (10) угол δ, при котором обеспечивается защемление стеблей в режущей паре при движении сегмента слева направо, можно вычислить следующим образом:
|
δ = arc tan (((B –b) / 2) / h′) – β + + arc tan (VC ∙ cos β / (VЖ – VC ∙ sin β)) < 90º. |
(11) |
Аналитические зависимости выражений (8) и (11) свидетельствуют о том, что угол защемления стеблей в режущей паре (δ) режущего аппарата, зависит от конструктивных параметров сегмента: нижнего (В) и верхнего (b) оснований, высоты режущей части (h′), а также угла поворота режущего аппарата относительно направления движения жатвенного агрегата (β), относительной скорости движения сегмента (VC) и скорости движения жатвенного агрегата (VЖ).
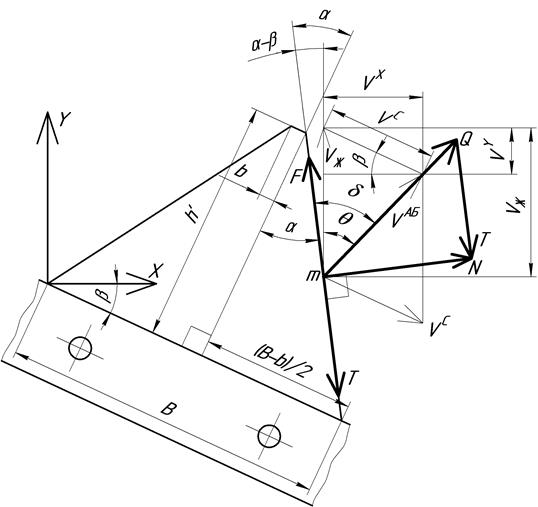
Рисунок 3. – Схема определения условия защемления стебля между сегментами режущего аппарата, развернутого на угол β относительно направления движения жатвенного агрегата при движении сегмента слева направо
При работе режущего аппарата, расположенного под углом (β) относительно направления движения жатвенного агрегата на условие защемления стебля в значительной степени будет влиять именно этот угол. Влияние угла (β) расположения режущего аппарата относительно направления движения жатвенного агрегата велико, так как помимо того, что значение этого угла в чистом виде входит в неравенства (3) и (9) он также опосредовано является составляющим в выражениях (4) и (10) при определении значения угла (θ) между вектором скорости жатвенного агрегата (VЖ) и вектором абсолютной скорости сегмента (VАБ), так как входит в состав выражений (5) и (6) при определении проекций вектора относительной скорости сегмента (VC) на оси Х (VX) и Y (VY).
Литература:
1. Кленин Н.И. Сельскохозяйственные и мелиоративные машины: Элементы теории рабочих процессов, расчет регулировочных параметров и режимов работы / Н.И. Кленин, В.А. Сакун. – М.: Колос, 1980. – 671 с.
2. Валковая жатка. Патент Р.Ф. № 2242858 2003 г. Воцкий З.И., Пермяков А.Ф., Боровинских Н.П., Грохотов А.С.







