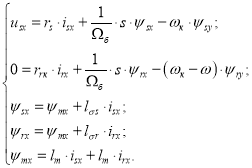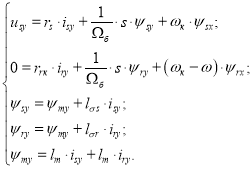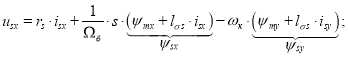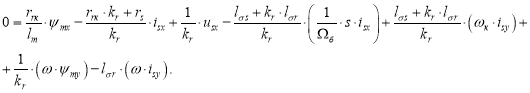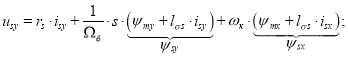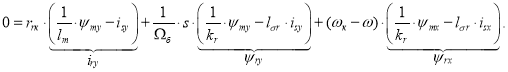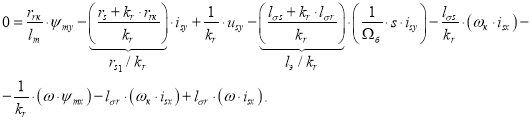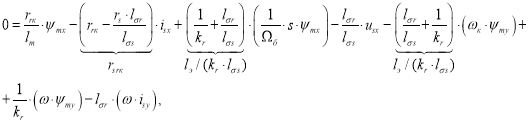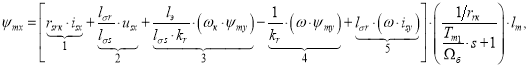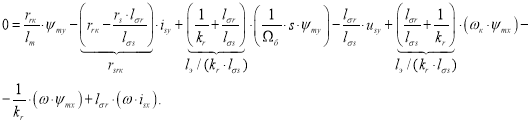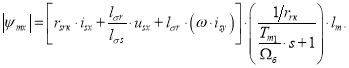Моделирование САР скорости системы «АИН ШИМ – АД» с переменными ψm – is с контуром потока в системе относительных единиц
Емельянов Александр Александрович, старший преподаватель;
Бесклеткин Виктор Викторович, старший преподаватель;
Соснин Александр Сергеевич, студент магистратуры;
Сучков Андрей Васильевич, студент
Российский государственный профессионально-педагогический университет (г. Екатеринбург)
Пестеров Дмитрий Ильич, студент магистратуры;
Забузов Евгений Игоревич, студент магистратуры;
Волков Егор Николаевич, студент магистратуры;
Камолов Икромиддин Иномидинович, студент магистратуры
Уральский государственный университет путей сообщения (г. Екатеринбург)
В этой статье рассмотрена САР скорости АД с контуром потока и синусоидальной ШИМ, являющаяся дальнейшим развитием работы [1].
В работе [1] приведены уравнения асинхронного двигателя по проекции x (+1):
|
|
(1) |
|
(2) |
|
|
(3) |
|
|
(4) |
|
|
(5) |
Из уравнения (5) выразим ![]() :
:
|
|
(6) |
Подставим ![]() в уравнение (4):
в уравнение (4):
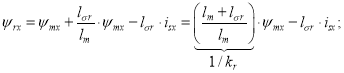
|
|
(7) |
Уравнения асинхронного двигателя по проекции y (+j):
|
|
(8) |
|
(9) |
|
|
(10) |
|
|
(11) |
|
|
(12) |
Аналогично выразим ![]() и
и ![]() :
:
|
|
(13) |
|
|
(14) |
Подставим уравнения (3) и (10) в (1):
|
|
(15) |
|
|
(16) |
Из уравнения (16) выразим ![]() :
:
|
|
(17) |
Подставим в уравнение (2) выражения ![]() ,
, ![]() и
и ![]() из уравнений (6), (7) и (14):
из уравнений (6), (7) и (14):
|
|
(18) |
Внесем в полученное уравнение выражение
|
|
(19) |
Обозначим ![]() и
и ![]() . Затем умножим уравнение (19) на
. Затем умножим уравнение (19) на ![]() и перенесем в левую часть слагаемые с переменной
и перенесем в левую часть слагаемые с переменной ![]() :
:
![]()
Обозначим ![]() и выразим
и выразим ![]() :
:
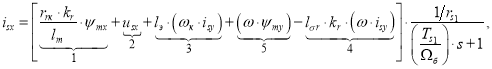
где ![]() - постоянная времени статорной обмотки в машинном (ЭВМ) времени;
- постоянная времени статорной обмотки в машинном (ЭВМ) времени;
![]() - постоянная времени статорной обмотки в реальном времени.
- постоянная времени статорной обмотки в реальном времени.
Структурная схема проекции статорного тока isx на ось +1 приведена на рис. 1.
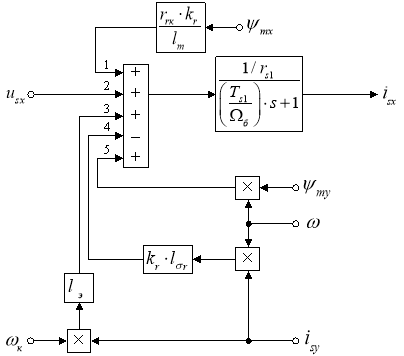
Рис. 1. Структурная схема проекции статорного тока isx на ось +1
Аналогично выразим ток isy по проекции y (+j).
Подставим уравнения (10) и (3) в (8):
|
|
(20) |
|
|
(21) |
Из уравнения (21) выразим ![]() :
:
|
|
(22) |
Подставим в уравнение (9) выражения ![]() ,
, ![]() и
и ![]() из уравнений (13), (14), (7):
из уравнений (13), (14), (7):
|
|
(23) |
Внесем в полученное уравнение выражение ![]() из (22):
из (22):
|
|
(24) |
Умножим обе части уравнения на ![]() и перенесем слагаемые с
и перенесем слагаемые с ![]() в левую часть:
в левую часть:
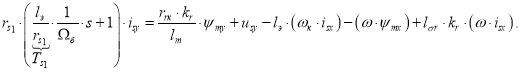
Отсюда ток ![]() :
:
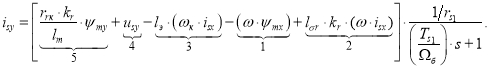
Структурная схема проекции статорного тока isy на ось +j приведена на рис. 2.
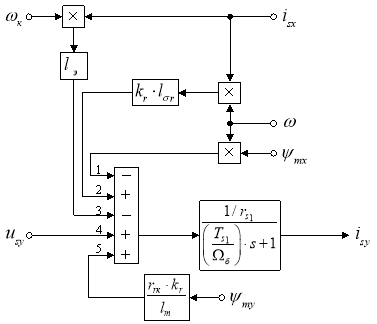
Рис. 2. Структурная схема проекции статорного тока isy на ось +j
Определим потокосцепление
Из уравнения (16) выразим ![]() :
:
|
|
(25) |
Подставим выражение (25) в уравнение (18):
|
|
(26) |
где ![]()
Перенесем в левую часть слагаемые с ![]() :
:
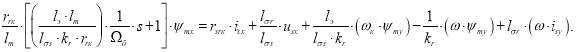
Обозначим ![]() и выразим
и выразим ![]() :
:
|
|
(27) |
где ![]() - постоянная времени потока в машинном (ЭВМ) времени;
- постоянная времени потока в машинном (ЭВМ) времени;
![]() - постоянная времени потока в реальном времени.
- постоянная времени потока в реальном времени.
Структурная схема проекции потокосцепления ψmx на ось +1 приведена на рис. 3.
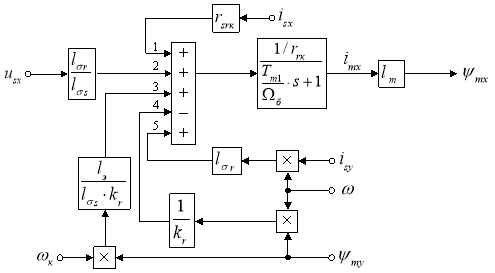
Рис. 3. Структурная схема проекции потокосцепления ψmx на ось +1
Аналогично определим потокосцепление ![]() по оси (+j).
по оси (+j).
Из уравнения (21) выразим ![]() :
:
|
|
(28) |
Подставим выражение (28) в уравнение (23):
|
|
(29) |
Перенесем в левую часть слагаемые с ![]() :
:
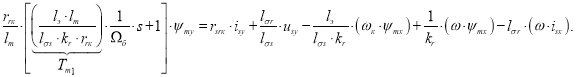
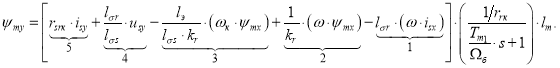
Структурная схема проекции потокосцепления ψmy на ось +j приведена на рис. 4.
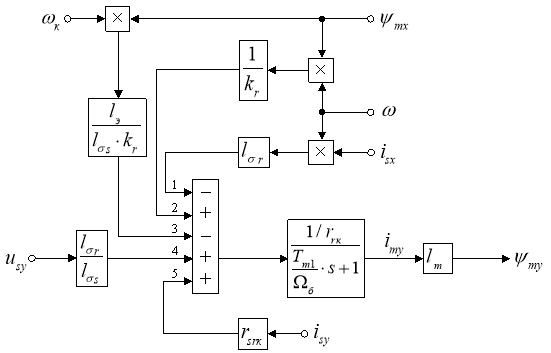
Рис. 4. Структурная схема проекции статорного тока ψmy на ось +j
На рис. 5 представлена структурная схема для реализации уравнения электромагнитного момента:

Рис. 5. Математическая модель определения электромагнитного момента m
Механическая угловая скорость вращения вала двигателя (рис. 6):
![]()
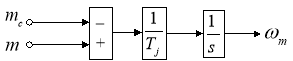
Рис. 6. Математическая модель определения механической угловой скорости вращения вала двигателя
Электрическая скорость вращения ротора (рис. 7):
![]()

Рис. 7. Математическая модель определения электрической скорости вращения ротора
Математическая модель асинхронного двигателя с короткозамкнутым ротором с переменными ψm – is на выходе апериодических звеньев приведена на рис. 8. Параметры асинхронного двигателя рассмотрены в работах [3] и [4].
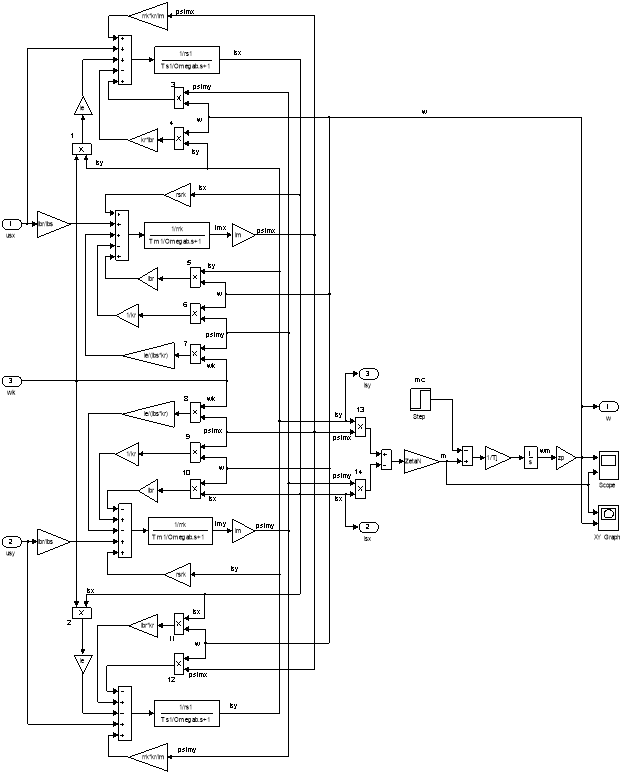
Рис. 8. Математическая модель асинхронного двигателя с переменными ψm – is на выходе апериодических звеньев
Развернутая схема САР скорости системы «АИН ШИМ – АД» приведена на рис. 9. Под каждым элементом схемы указаны его номер и название.
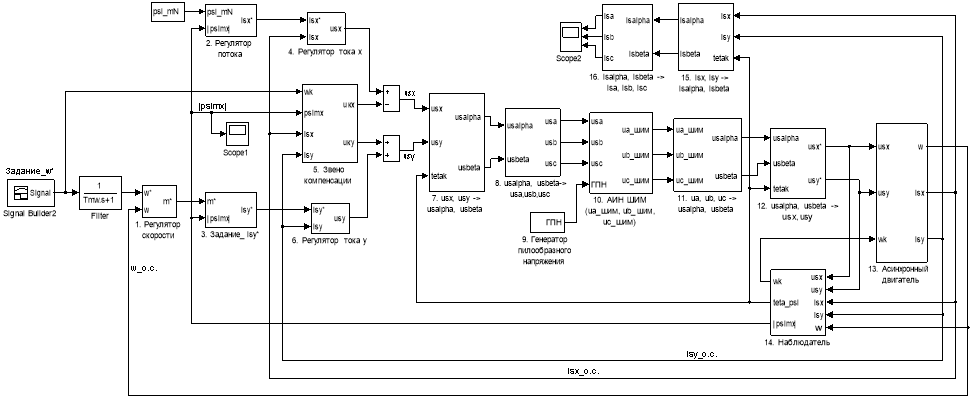
Рис. 9. Развернутая математическая модель САР скорости системы «АИН ШИМ – АД»
В контурах тока по проекциям x и y были получены одинаковые передаточные функции объектов управления:
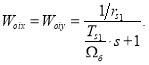
Синтез регуляторов тока производится по классической схеме [2]:
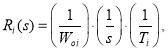
где ![]() - компенсация объекта;
- компенсация объекта;
![]() - введение новой постоянной времени контура тока.
- введение новой постоянной времени контура тока.
Передаточная функция фильтра:
![]()
Принимаем настройку на модульный оптимум ![]() , тогда передаточные функции регуляторов тока по проекциям x и y:
, тогда передаточные функции регуляторов тока по проекциям x и y:
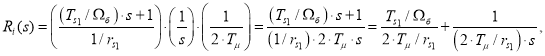
где Tμ - некомпенсируемая постоянная времени (примем Tμ = 0,0025 с).
Обозначим:
![]()
![]()
Математические модели ПИ-регуляторов тока по проекциям x и y под номерами 4 и 6 приведены на рис. 10 и 11.
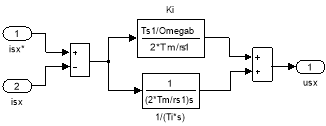
Рис. 10. ПИ-регулятор тока по проекции x
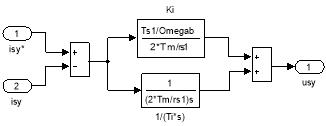
Рис. 11. ПИ-регулятор тока по проекции y
Важной частью структуры является наблюдатель, который служит для вычисления амплитуды и углового положения вектора потокосцепления. Поскольку в системе x, y поток ориентирован по оси x, определим модуль |ψmx|, исключив из уравнения (27) составляющую потока ψmy:
|
|
(30) |
Из уравнения (29) выразим ![]() при ψmy = 0:
при ψmy = 0:
![]()
![]()
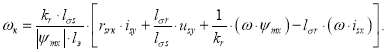
Интегрируя ![]() , можно получить угол потока ψmx [6].
, можно получить угол потока ψmx [6].
Математическая модель наблюдателя потокосцепления ψmx (номер 14) приведена на рис. 12.
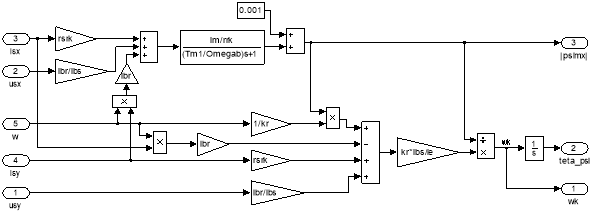
Рис. 12. Модель наблюдателя потокосцепления ψmx
При определении регулятора потокосцепления учтем следующее:
‒ до тех пор, пока поток ![]() не установится, нельзя включать сигнал задания на задатчик интенсивности, т.е. ω = 0;
не установится, нельзя включать сигнал задания на задатчик интенсивности, т.е. ω = 0;
‒ напряжение ![]() близко к нулю.
близко к нулю.
В этом случае уравнение (30) примет следующий вид:
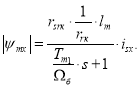
Следовательно, передаточной функцией потока является:
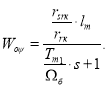
Синтез регулятора потока:
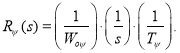
Примем
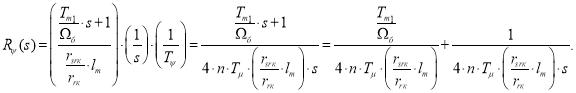
Выразим коэффициенты ПИ-регулятора потока:
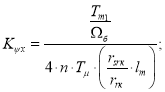
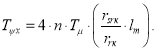
Модель ПИ-регулятора потока под номером 2 представлена на рис. 13.
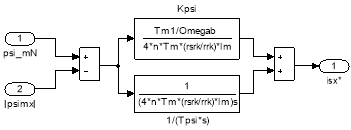
Рис. 13. ПИ-регулятор потока
Выполним синтез регулятора скорости.
С учетом наблюдателя (![]() ) уравнение момента примет вид:
) уравнение момента примет вид:
![]()
Причем к моменту включения задатчика интенсивности
Приведем структурную схему контура скорости (рис. 14).
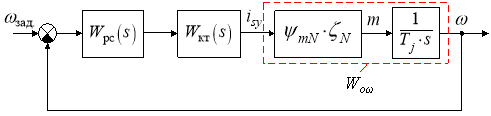
Рис. 14. Структурная схема контура скорости
В контуре скорости передаточная функция объекта имеет следующий вид:
![]()
Синтез регулятора скорости:
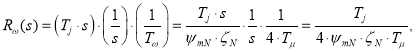
где![]()
Математическая модель П-регулятора скорости (номер 1) приведена на рис. 15.
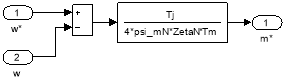
Рис. 15. Пропорциональный регулятор скорости
В системе управления предусмотрена компенсация внутренних перекрестных связей. Из уравнений (15) и (20) выразим компенсационные составляющие каналов управления:
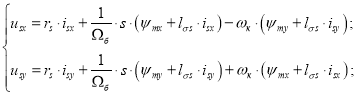
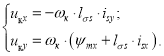
Математическая модель компенсации перекрестных связей (номер 5) представлена на рис. 16.
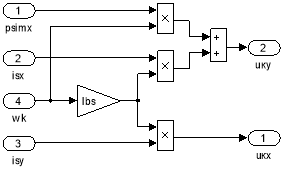
Рис. 16. Компенсация внутренних перекрестных связей
Задание на скорость ω* формируется в блоке Signal Builder (рис. 17).
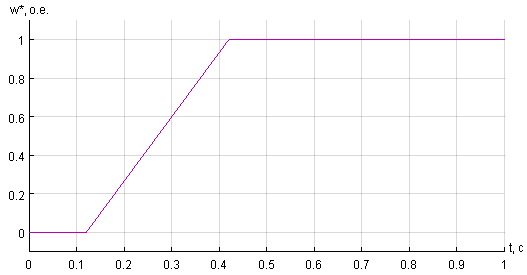
Рис. 17. Сигнал задания на скорость ω*
Задание на статорный ток по проекции y:
Отсюда ![]()
Математическая модель определения задания ![]() (номер 3) дана на рис. 18.
(номер 3) дана на рис. 18.
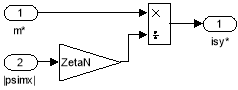
Рис. 18. Реализация задания статорного тока ![]() по проекции y
по проекции y
Преобразователи координат на развернутой схеме САР скорости под номерами 7 и 8 (![]() и
и ![]() ) приведены на рис. 19 и 20 [4].
) приведены на рис. 19 и 20 [4].
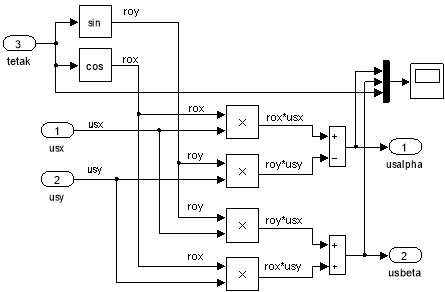
Рис. 19. Преобразователь координат: usx, usy → usα, usβ
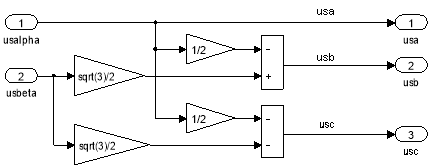
Рис. 20. Преобразователь координат: usα, usβ → usa, usb, usc
Математические модели АИН ШИМ (номер 10) и генератора пилообразного напряжения ГПН (номер 9) даны на рис. 21 и 22. Работа АИН ШИМ была рассмотрена нами в статьях за 2016 г.

Рис. 21. Генератор пилообразного напряжения (ГПН)
Преобразователи координат под номерами 11 и 12 (![]() и
и ![]() ) даны на рис. 23 и 24.
) даны на рис. 23 и 24.
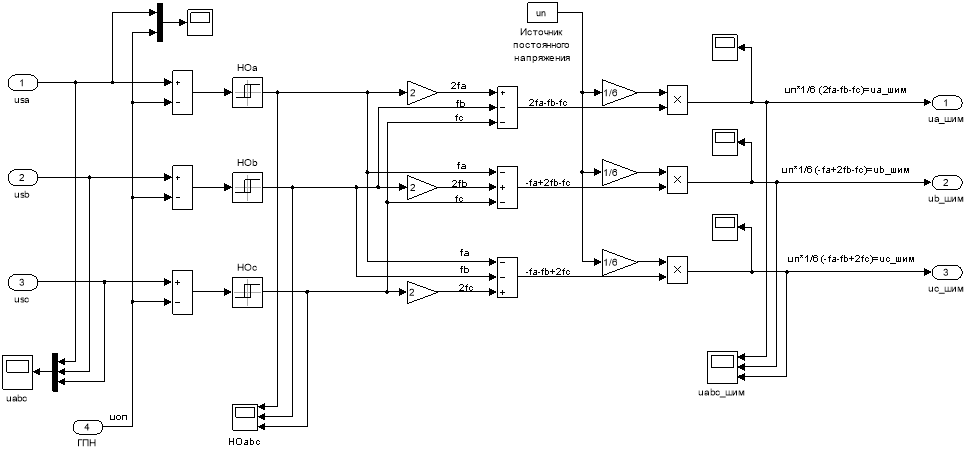
Рис. 22. Математическая модель АИН ШИМ
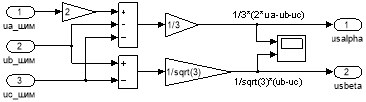
Рис. 23. Преобразователь координат: uа шим, ub шим, uc шим → usα, usβ
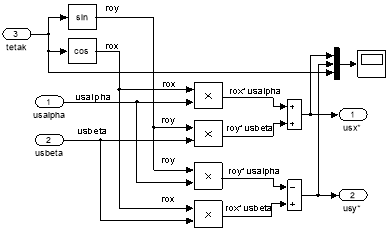
Рис. 24. Преобразователь координат: usα, usβ → usx, usy
Обратные преобразователи координат по статорным токам с номерами 15 и 16 на развернутой схеме САР скорости приведены на рис. 25 и 26 [4].
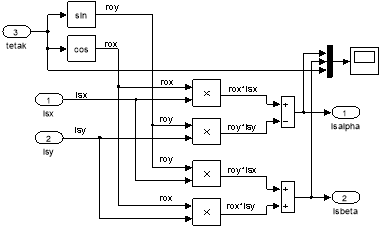
Рис. 25. Обратное преобразование (1-я ступень): isx, isy → isα, isβ
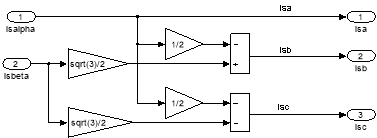
Рис. 26. Обратное преобразование (2-я ступень): isα, isβ → isa, isb, isc
Расчет параметров производим в Script:
|
PN=320000; UsN=380; IsN=324; fN=50; Omega0N=104.7; OmegaN=102.83; nN=0.944; cos_phiN=0.92; zp=3; Rs=0.0178; Xs=0.118; Rr=0.0194; Xr=0.123; Xm=4.552; J=28; |
Ub=sqrt(2)*UsN; Ib=sqrt(2)*IsN; OmegasN=2*pi*fN; Omegab=OmegasN; Omegarb=Omegab/zp; Zb=Ub/Ib; kd=1.0084; Mb=kd*PN/OmegaN; Pb=Mb*Omegarb; rs=Rs/Zb; lbs=Xs/Zb; lbr=Xr/Zb; lm=Xm/Zb; kr=lm/(lm+lbr); Tj=J*Omegarb/Mb; |
betaN=(Omega0N-OmegaN)/Omega0N; SsN=3*UsN*IsN; ZetaN=SsN/Pb; roN=0.9962; rrk=roN*betaN; Tm=0.0025; Tmw=0.005; psi_mN=0.9472; n=20; un=2.2; le=lbs+kr*lbr; rs1=kr*rrk+rs; rsrk=rrk-rs*lbr/lbs; Ts1=le/rs1; Tm1=lm*le/(rrk*kr*lbs); |
Числовые значения параметров выводятся в окне Workspace (рис. 27).
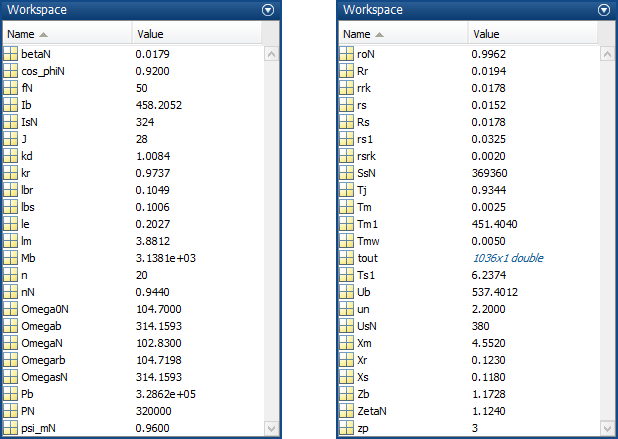
Рис. 27. Числовые значения параметров в окне Workspace
Результаты моделирования САР скорости системы «АИН ШИМ – АД» приведены на рис. 28, …, 31.
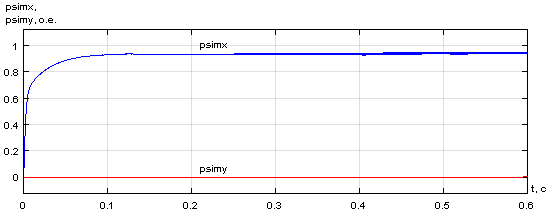
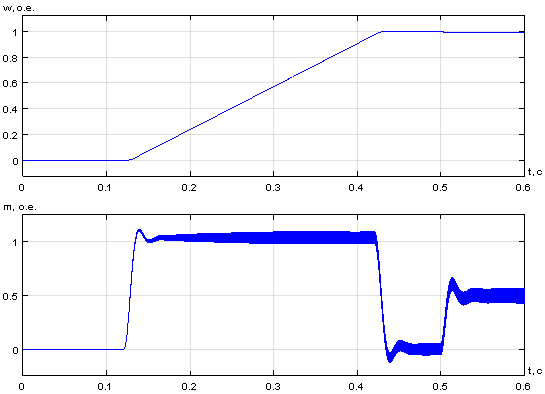
Рис. 28. Графики потокосцеплений, скорости и электромагнитного момента при ![]() и fоп = 10 кГц
и fоп = 10 кГц
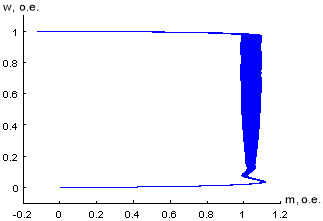
Рис. 29. Динамическая механическая характеристика при ![]() и fоп = 10 кГц
и fоп = 10 кГц
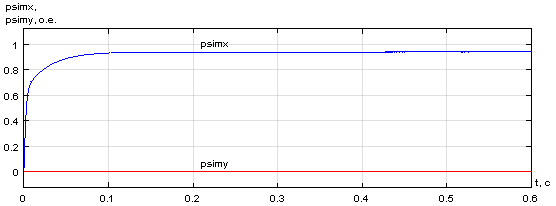
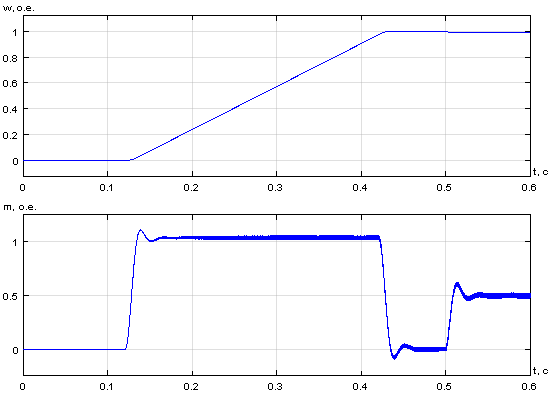
Рис. 30. Графики потокосцеплений, скорости и электромагнитного момента при ![]() и fоп = 30 кГц
и fоп = 30 кГц
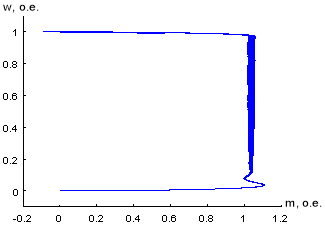
Рис. 31. Динамическая механическая характеристика при ![]() и fоп = 30 кГц
и fоп = 30 кГц
Литература:
- Емельянов А.А., Бесклеткин В.В., Корнильцев А.Г., Факеев Д.Г., Маклыгин К.А., Логинов А.В., Коновалов И.Д., Антоненко И.А., Пестеров Д.И. Моделирование САР скорости асинхронного двигателя с переменными ψm – is с контуром потока в системе относительных единиц // Молодой ученый. — 2018. — №40. — С. 6-25.
- Шрейнер Р.Т. Системы подчиненного регулирования электроприводов: учеб. пособие / Р.Т. Шрейнер. - Екатеринбург: Изд-во ГОУ ВПО «Рос. гос. проф.-пед. ун-т», 2008. – 279 с.
- Шрейнер Р.Т. Электромеханические и тепловые режимы асинхронных двигателей в системах частотного управления: учеб. пособие / Р.Т. Шрейнер, А.В. Костылев, В.К. Кривовяз, С.И. Шилин. Под ред. проф. д.т.н. Р.Т. Шрейнера. - Екатеринбург: ГОУ ВПО «Рос. гос. проф.-пед. ун-т», 2008. - 361 с.
- Шрейнер Р.Т. Математическое моделирование электроприводов переменного тока с полупроводниковыми преобразователями частоты. – Екатеринбург: УРО РАН, 2000. - 654 с.
- Шрейнер Р.Т. Электроприводы переменного тока на базе непосредственных преобразователей частоты с ШИМ: монография / Р.Т. Шрейнер, А.И. Калыгин, В.К. Кривовяз; под. ред. Р.Т. Шрейнера. - Екатеринбург: ФГАОУ ВПО «Рос. гос. проф.-пед. ун-т», 2012. – 223 с.
- Калачёв Ю.Н. Наблюдатели состояния в векторном электроприводе. - М.: Самиздат, 2015. - 80 с.