Целью работы является исследование планетарной передачи и кинематический анализ передачи.
Ключевые слова: зубчатое колесо (шестеренка), солнечная шестерня, кольцевая шестерня (корона), сателлит, водило, эпицикл, редуктор, коробка скоростей.
Планетарная передача – механическая передача вращательного движения, имеющая зубчатое колесо с подвижными геометрическими осями. Подвижность оси обеспечивает компактность механизма и уменьшает массу (или габариты) передачи. Можно получить систему с двумя и более степенями свободы, которая расширяет применение планетарной передачи в различных технологических и транспортных машинах.
Принцип действия планетарных передач основан на вращении зубчатых колес (шестеренок) и представляет собой несколько взаимосвязанных шестеренок (Рис.1).
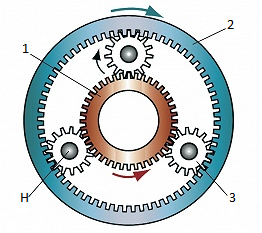
Рис. 1. 1 - солнечная шестерня, 2 - кольцевая шестерня (корона), 3 - сателлиты, Н - водило
- Солнечная (центральная) шестерня находится в центре;
- Кольцевая шестерня (корона): внешнее зубчатое колесо, имеющее внутреннее зацепление с планетарными шестернями. Также ее называют «эпициклом» планетарной передачи;
- Планетарная шестерня (сателлиты) одиночного размера, находящаяся в зацеплении с солнечной шестерней. Число сателлитов в планетарных передачах варьируется от 2 до 6, в зависимости от возможности размещения в механизме, чаще встречаются механизмы с тремя сателлитами, что обеспечивает более равномерное распределение нагрузок. Зубчатые колеса планетарной передачи могут быть любого известного типа из курса «Детали машин»: прямозубые, косозубые, червячные, шевронные. Тип зацепления не оказывает влияния на работу планетарной передачи.
- Одним из основных элементов планетарной передачи является водило – (Н) – подвижное звено, на котором жестко фиксированы друг относительно друга оси нескольких сателлитов.
После ознакомления с основными деталями планетарной передачи возникает вопрос: а почему подобные механизмы называют планетарными? Ответ простой: сателлиты вращаются вокруг своих осей и вместе с осью – вокруг солнечной шестерни, т. е. совершают движение, подобное движению планет. Отсюда название - планетарные передачи. В международных энциклопедиях встречаются синонимы подобных механизмов: планетарная, дифференциальная или эпициклическая передача.
Как все передаточные механизмы, планетарные передачи служат для преобразования кинематических параметров и передачи движения от двигателя другим механизмам машин. Планетарная передача способна в пределах одной оси изменять, складывать и раскладывать угловые скорости и крутящий момент.
Основной кинематической характеристикой планетарной передачи является передаточное отношение (u). Передаточное отношение такой передачи визуально определить очень сложно, потому что механизм может вращаться различными способами, и для кинематического исследования передачи существуют аналитический и графический методы.
Аналитический метод определения передаточного отношения основан на способе обращения движения, который впервые предложил английский ученый Виллис, поэтому аналитический метод больше всего известен под названием «метод Виллиса».
Суть метода заключается в следующем.
Всей планетарной передаче сообщается дополнительное вращение с угловой скоростью – 
, равной угловой скорости водила, но обратной направлению. Таким образом, водило Н останавливается, а другие колеса освобождаются; колесо 3 (корона) было неподвижно, а в преобразованном механизме начинается вращаться с угловой скоростью . Обычный планетарный механизм (рис.2,а) превратится в обращенный механизм (рис.2,б)
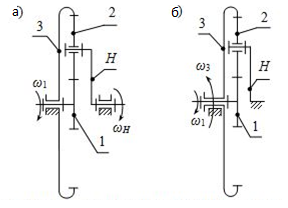
Рис. 2. 1 - ведущее центральное колесо; 2 - сателлит; 3 - неподвижное центральное колесо; Н - водило
Звенья обращенного механизма будут вращаться с угловыми скоростями:
; 
; 
Математическое описание передаточного отношения может быть выражено через отношение чисел зубьев (z), угловых скоростей (
), частот вращения (n).
Определим передаточное отношение:
а) через угловые скорости:
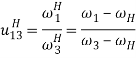
Но поскольку мы знаем, что 3-звено – это неподвижное центральное колесо (ω3 = 0), то получаем
Отсюда найдем аналогичную формулу для определения передаточного отношения планетарного механизма:
Эта формула справедлива для любой схемы планетарного механизма при наличии неподвижного центрального колеса. Значит, и передаточное отношение от любого планетарного колеса 
водилу Н при неподвижном опорном колесе j ровно единице минус передаточное отношение 
от этого же колеса к опорному (центральному) в обращенном механизме, т. е.
= 
,
или
+ 
= 1.
Таким образом, для планетарных механизмов с круглыми колесами сумма передаточных отношений при различных останавливаемых звеньях всегда равна единице.
б) через количество зубьев (z):
; 
;
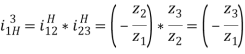
в) через частоты вращения (n):
Частоты вращения зубчатых колес обращенного механизма равны разности прежних частот вращения и частоты вращения водила. Допустим, 
, 
, 
- частоты вращения соответственно звеньев 1, 3, Н; а 
- означает передаточное отношение с направлением движения от 1 к 3 при неподвижном Н. Для обращенного механизма получаем следующую формулу:
= 
В реальной ситуации колесо 3 заторможено (= 0), тогда
= 
= 
Широкие кинематические возможности планетарной передачи позволяют использовать данную передачу как редуктор с постоянным передаточным отношением; как коробку скоростей или как дифференциальный механизм.
Литература:
- Иосилевич Г. Б., Строганов Г. Б., Маслов Г. С. Прикладная механика. — М.: Высшая школа, 1989.
- Иванов М. Н., Детали машин. — М.: Высшая школа, 1991.
- Фролов К. В., Попов С. А., Мусатов А. К. и др. Теория механизмов и машин. — М.: Высшая школа, 1987.
