В статье приводятся результаты конечно-элементного моделирования и оценки начального напряженно-деформированного состояния (НДС) гнутоклееной балки. Начальное НДС гнутоклееной балки возникает в процессе изготовления: изгиба отдельных слоев, их склеивания, запрессовки и распрессовки склеенной балки. В результате процесса изготовления в балке реализуются начальные радиальные, тангенциальные и касательные напряжения, которые необходимо учитывать в расчетах балки на эксплуатационные нагрузки. Конечно-элементное (КЭ) моделирование и анализ НДС балки выполняются в программном комплексе ANSYS. КЭ моделирование позволяет учесть все особенности и этапы изготовления, анизотропию физико-механических свойств древесины и, как следствие, исключить трудоемкие натурные испытания.
Ключевые слова: гнутоклееная деревянная балка, начальное НДС, радиальные, тангенциальные и касательные напряжения, метод конечных элементов, программный комплекс ANSYS.
Keywords: glulam curved wooden beam, initial stress-strain state, radial, tangential and shear stress, finite element method, software ANSYS.
Процесс изготовления деревянных гнутоклееных балок состоит из двух этапов:
– изгиба каждого отдельного слоя на расчетную кривизну с нанесением клея на поверхности и последующей запрессовки всех слоев пакета;
– распрессовка склеенного пакета после высыхания клея.
В результате процесса изготовления в балке реализуются начальное НДС, которое может оказывать существенное влияние на дальнейшую эксплуатацию всей конструкции. Современные нормативно-технические документы не дают рекомендаций по оценке начального НДС деревянных гнутоклееных балок [1], а проведение натурных испытаний является весьма трудоемким и дорогостоящим. В связи с этим применение численного моделирования процесса изготовления гнутоклееной балки с использованием современных КЭ комплексов является актуальным и позволяет оценить преднапряженное состояние с высокой точностью.
В качестве объекта исследования рассматривается пакет из десяти слоев. Каждый слой имеет толщину 30 мм, длину 3000 мм и ширину 100 мм. Геометрическая модель (CAD-модель) пакета в первоначальном состоянии приведена на рисунке 1. Под первоначальным состоянием пакета принимается состояние, в котором все слои прямые.

Рис. 1. Геометрическая модель пакета
Древесина является анизотропным материалом, физико-механические свойства которого отличаются для различных направлений (вдоль и поперек волокон). В современных методиках расчета деревянных конструкций в качестве материала принято использовать ортотропную модель — частный случай анизотропной модели, при котором учитывается неоднородность свойств по трем взаимно перпендикулярным направлениям. В настоящей работе используется ортотропная модель древесины с физико-механическими свойствами в соответствии с [1], [2], которые приведены в таблице 1.
Таблица 1
Ортотропные свойства древесины
|
|
|
|
|
|
|
|
|
|
|
12000 |
400 |
400 |
0,45 |
0,45 |
0,33 |
500 |
500 |
500 |
|
Примечания: |
||||||||
Индексы «1», «2», «3» в таблице 1 соответствуют осям локальной системы координат одного слоя, которая приведена на рисунке 2.
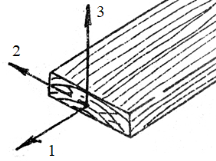
Рис. 2. Локальная система координат одного слоя
КЭ расчет состоит из двух шагов, соответствующих двум этапам изготовления деревянных гнутоклееных балок. Граничные условия для каждого шага расчета приведены в таблице 2.
Таблица 2
Граничные условия
|
Шаг расчета (этап изготовления) |
Граничные условия |
|
«1» (изгиб каждого слоя и их запрессовка между собой) |
Приложение к торцам каждого слоя кинематических условий — углов поворота ±14,5° (что соответствует радиусу кривизны слоя 6000 мм) Создание контактных пар между слоями, в которых учитывается только контактное давление (без трения) |
|
«2» (распрессовка склеенного пакета) |
Исключение из расчета кинематических условий и контактных пар на шаге расчета «1» Учет собственного веса конструкции Создание «идеальных» контактных пар между слоями, которые обеспечивают совместность деформаций слоев |
Для получения корректного НДС гнутоклееной балки большой кривизны в КЭ расчете учитывается влияние геометрической нелинейности, алгоритм которой в процессе решения позволяет учитывать изменение матрицы жесткости под влиянием изменения формы конструкции.
КЭ сетка модели выполнена с использованием 20-ти узловых гексаэдральных элементов и приведена на рисунке 3. Количество конечных элементов модели составляет 375000, количество узлов сетки — 1201050. Тип конечных элементов имеет квадратичную функцию формы, что совместно с принятым количеством узлов обеспечивает сходимость метода конечных элементов и высокую точность полученных результатов.

Рис. 3. КЭ сетка
В результате проведенного расчета получены распределения модуля вектора перемещений (суммарных перемещений, мм), радиальных и тангенциальных напряжений (МПа), которые приведены на рисунках 4 — 6 соответственно. На рисунках 5, 6 также указано характерное сечение балки, вдоль которого приводятся зависимости напряжений. Характерное сечение балки выбрано вдали от краевых эффектов, полученных в результате конечно-элементного решения.
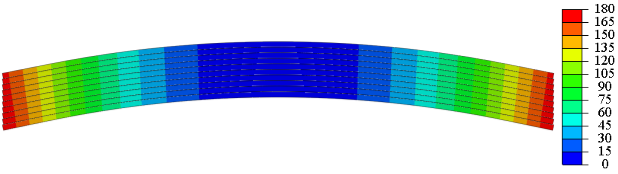
Рис. 4. Распределение модуля вектора перемещений, мм
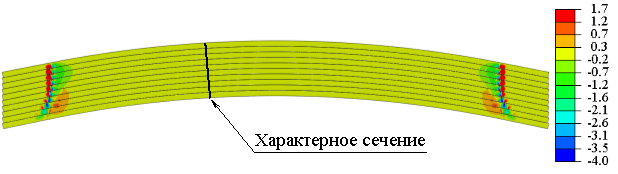
Рис. 5. Распределение радиальных напряжений, Мпа
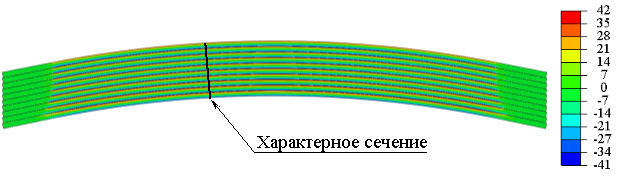
Рис. 6. Распределение тангенциальных напряжений, Мпа
Неоднородность распределения радиальных напряжений и отсутствие тангенциальных напряжений на краях балки вызваны краевым эффектом из-за особенностей численного моделирования контактного взаимодействия между слоями.
Зависимости радиальных и тангенциальных напряжений по высоте балки в характерном сечении приведены на рисунках 7, 8 соответственно. На графиках рисунков 7, 8 на осях ординат показаны толщины слоев балки в мм, на осях абсцисс — значения напряжений в МПа. Значение 0 мм соответствует нижней поверхности первого слоя, 300 мм — верхней поверхности десятого слоя.
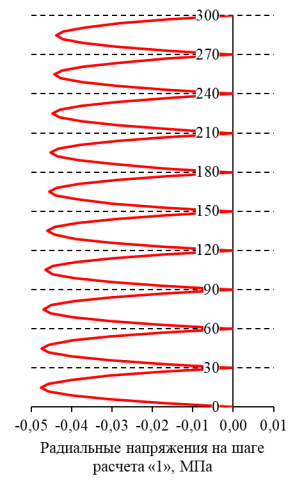
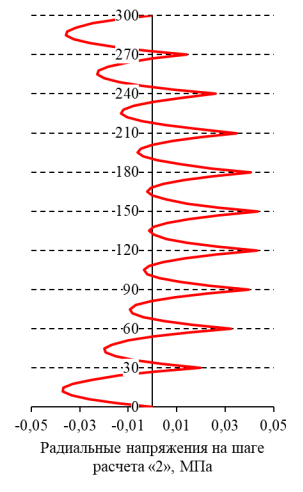
Рис. 7. Распределения радиальных напряжений по характерному сечению
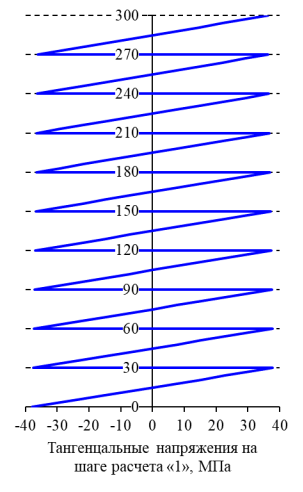
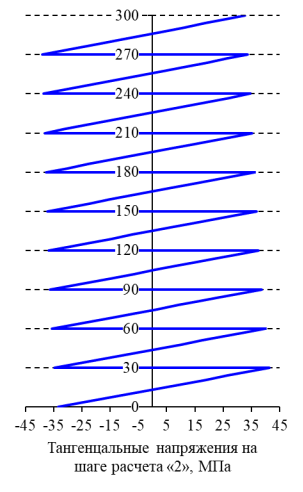
Рис. 8. Распределение тангенциальных напряжений по характерному сечению
Значения касательных напряжений на стыках слоев гнутоклееного балки приведено в таблице 3.
Таблица 3
Значения касательных напряжений
|
Стык между слоями |
1–2 |
2–3 |
3–4 |
4–5 |
5–6 |
6–7 |
7–8 |
8–9 |
9–10 |
|
Касательное напряжение, МПа |
0,159 |
0,162 |
0,164 |
0,165 |
0,167 |
0,168 |
0,170 |
0,172 |
0,173 |
Из графиков на рисунках 7, 8 и таблицы 3 видно, что в процессе изготовления гнутоклееной балки возникает преднапряженное состояние: радиальные, тангенциальные и касательные напряжения. Радиальные напряжения достигают максимальных значений на стыках центральных слоев. Максимальные тангенциальные растягивающие напряжения реализуются на выпуклых поверхностях слоев пакета, максимальные сжимающие — на вогнутых поверхностях слоев пакета. Полученное решение коррелирует с результатами работы [3].
Преднапряженное состояние гнутоклееной балки важно учитывать, т. к. оно будет оказывать влияние на дальнейшую её эксплуатацию. Например, в случае действия эксплуатационных нагрузок, которые вызывают разгибание балки, наиболее опасными будут радиальные растягивающие напряжения [4], которые в сумме с начальными напряжениями увеличивают опасность разрыва балки поперек волокон.
Литература:
- СП 64.13330.2017 Деревянные конструкции. Актуализированная редакция СНиП II-25–80 (с Изменением N 1): нормативно-технический материал. — Москва: Стандартинформ, 2017. — 97 с.
- Petra Steen. Structural Design of a Wooden Wind Tower Structure: Master’s thesis in Applied Mechanics, 2017. — Chalmers University of Technology, Gothenburg, Sweden — 67 p.
- Шмидт А. Б. О преднапряженном состоянии деревянного гнутоклееного элемента большой кривизны / А. Б. Шмидт // Материалы 9-й Международной научно-практической конференции «Инновации в деревянном строительстве». — Санкт-Петербург: СПбГАСУ, 2018. — С.81–86.
- Лехницкий С. Г. Теория упругости анизотропного тела / С. Г. Лехницкий. — Москва: Наука, 1977. — 416 с.







