Приведены исследования синхронного двигателя; даны рекомендации по моделированию процессов синхронного двигателя.
Ключевые слова: синхронные двигатели ротора управление закону Кирхгофа моделирование.
Введение. В настоящее время широко распространены различные синхронные двигатели Синхронные двигатели по конструктивному исполнению ротора делятся на два типа: с явно- и неявновыраженными полюсами, а по типу возбуждения ротора — с электромагнитным и магнитоэлектрическим возбуждением [1,2]. В последнем случае ротор выполняется неявнополюсным, а его возбуждение осуществляется от постоянного магнита. Двигатели с постоянными магнитами находят наибольшее применение в приводах систем автоматики мощностью до нескольких киловатт, как будет показано ниже, на основе таких машин строятся находящие все большее применение вентильные двигатели постоянного тока малой мощности. Рассмотрим построение математической модели двигателя. Управление электрической цепи фазы индукторного двигателя по второму закону Кирхгофа [3,4].
При составлении уравнений синхронной машины удобно описывать их в системе координат, связанных с обмотками ротора. В воздушном зазоре находится неподвижное относительно ротора магнитное поле, созданное переменными токами обмоток статора. Картина не изменится, если остановить ротор и магнитное поле. Чтобы в заторможенной машине токи остались теми же, что и во вращающейся, надо ввести ЭДС вращения в обмотки якоря, частоту токов сделать равной нулю [5,6].
Напряжение на двигателе описывается уравнением
![]() (1)
(1)
Здесь противоЭДС определяется по закону электромагнитной индукции:
![]() (2)
(2)
где ![]() - потокосцепление фазы индуктивного двигателя,
- потокосцепление фазы индуктивного двигателя, ![]() - индуктивность катушки,
- индуктивность катушки, ![]() - линейная скорость,
- линейная скорость, ![]() - частная производная потока сцепления по линейному перемещению при постоянном токе.
- частная производная потока сцепления по линейному перемещению при постоянном токе.
Подставим выражение (2) для противоЭДС в уравнение (1) и преобразуем его к виду Коши:
![]() (3)
(3)
Механическое управление движения якоря на основании второго закона Ньютона имеет вид:
![]() (4)
(4)
где ![]() - масса якоря,
- масса якоря, ![]() - электромагнитная сила,
- электромагнитная сила, ![]() - сила сопротивления.
- сила сопротивления.
Понизим порядок дифференциального уравнения (4), введя промежуточное уравнение:
![]()
![]() (5)
(5)
Общая математическая модель четырёхфазного двигателя, составленная по уравнениям (3) и (5), имеет вид:
![]()
![]() (6)
(6)
![]()
![]() (7)
(7)
![]()
![]() (8)
(8)
В уравнениях (6) и (7) используются величины частных производных потокосцеплений:
![]()
![]() (9)
(9)
Поскольку магнитные системы фаз между собой не связаны, их потокосцепления и электромагнитные силы являются функциями линейного перемещения и тока соответствующей фазы:
![]()
![]() (10)
(10)
Для определения функций (10) предлагается разложить их в гармонический ряд по координате линейного перемещения с послкдующей аппроксимацией амплитуд каждой гармоники полиномами Чебышева на множестве равноудалённых точек по координате тока фазы, используя результаты вычислительных Экспериментов как исходные данные. При этом аппроксимация потокосцепления фазы имеет вид:
![]()
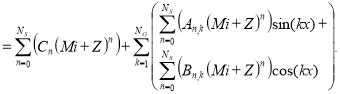 (11)
(11)
где ![]() ,
, ![]() и
и ![]() — полиномы Чебышева при синусной, косинусной и постоянной составляющих соответственно,
— полиномы Чебышева при синусной, косинусной и постоянной составляющих соответственно, ![]() — номер гармоники,
— номер гармоники, ![]() — число гармоник,
— число гармоник, ![]() и
и ![]() — коэффициенты регрессии полиномов при синусной, косинусной и постоянной составляющих соответственно,
— коэффициенты регрессии полиномов при синусной, косинусной и постоянной составляющих соответственно, ![]() — номер коэффициента регрессии,
— номер коэффициента регрессии, ![]() — степень полинома,
— степень полинома, ![]() и
и ![]() — масштабный коэффициент и смещение при токе фазы.
— масштабный коэффициент и смещение при токе фазы.
Аналогично потокосцеплению представим аппроксимацию электромагнитной силы:
![]()
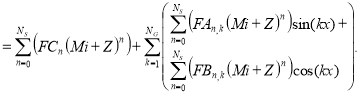 (12)
(12)
где
Выводы. Таким образом, синхронный двигатель представляет собой динамическую систему четвертого порядка. Установившаяся ошибка по скорости равна нулю, что согласуется с принципом действия двигателя. В большинстве случаев на роторе синхронного двигателя имеется короткозамкнутая пусковая или демпферная обмотка. Наличие их не изменит порядка системы, а повлияет только на значения некоторых коэффициентов передаточной функции. В частности, увеличится коэффициент передачи, что способствует повышению устойчивости двигателя. В общем случае о динамической устойчивости двигателя необходимо судить по характеристическому уравнению, исследуя его известными методами теории автоматического управления. В практике иногда встречаются сочетания параметров, при которых двигатель оказывается неустойчивым. Для обеспечения устойчивости вводят регулирование возбуждения или обратную связь по положению ротора.
Литература:
- Tony R. Kuphaldt. Lessons In Electric Circuits, Volume II — AC, Sixth Edition, 2007. — 561 с.
- Брускин Д. Э., Зорохович А. Е., Хвостов В. С. Электрические машины и микромашины: Учеб.для электротехн. спец. вузов. — 3-е изд., перераб. и доп. — М.: Высш. шк., 1990. — 528 с.
- Дискретный электропривод с шаговыми двигателями. Под общ.ред. М. Г. Чиликина. М., «Энергия», 1971. — 624 c.
- Ion Boldea. Electric drives. — Lexington, KY, USA — 2005, — 549 с.
- Чиликин М. Г., Сандлер А. С. Общий курс электропривода: Учебник для вузов. — 6-е изд., доп. и перераб. — М.: Энергоиздат, 1981. — 576 с.
- Теория электропривода, ч.1: учебное пособие / Сост.: А. Б. Зеленов — Алчевск, ДонГТУ, 2005. — 382 с.







