In the work, problem of object recognition by application of neural networks based on algorithm of backpropagation on the example of recognition of geometrical objects — triangles, rectangles and circles, was considered.
For the solution of the problem of recognition of geometrical shapes on multilayered perceptron network architecture it was used a backpropagation algorithm. Neural network is divided into input, hidden and output layers, which consist of 784, 300, 3 neurons respectively. Image 28x28 sized (matrix ![]() ) is used for the input. Neurons on the output layer provide the probability of the recognition. Learning the network is divided into several stages, which includes:
) is used for the input. Neurons on the output layer provide the probability of the recognition. Learning the network is divided into several stages, which includes:
‒ Data submission to the input layer and getting an output;
‒ Calculating and propagating an appropriate error;
‒ Correction of the weights;
Implementation of the neural network using backpropagation algorithm was realized on Python. For learning of the neural network Keras library was used. As a result, learning coefficient on the output — 0.90. Subsequently, recognition probability equals to 90 %.
Let us take ![]() — an input vector of the learning data,
— an input vector of the learning data, ![]() — weights vector, each element of which corresponds to the each neuron,
— weights vector, each element of which corresponds to the each neuron, ![]() — vector of hidden neurons,
— vector of hidden neurons, ![]() — vector of output neurons,
— vector of output neurons, ![]() error information,
error information, ![]() — weight correction component of
— weight correction component of![]() ,
, ![]() bias,
bias, ![]() — vector of target values.
— vector of target values.
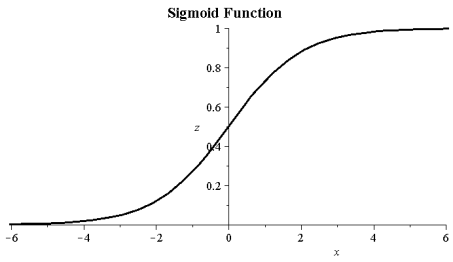
Activation function
Activation function should be continuous, differential and monotonously decreasing. Let us consider binary sigmoid activation function with (0, 1) range, which can be defined by following formula:
Learning algorithm
-
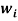 weights initialization between neurons
weights initialization between neurons
Weights initialization is set up stochastic and accepts discrete random variants from Normal distribution ![]()
![]()
![]() 1;
1;
- Data distribution from the input towards to the output.
Each input neuron gets input signal![]() . Firstly, signal quantity should be determined, which is the product of rows and cols of matrix I:
. Firstly, signal quantity should be determined, which is the product of rows and cols of matrix I:
![]()
![]()
-
Each input neuron
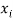 transmits obtained input data to the all neurons on the hidden layer. Input data is the sum of all signals multiplied to appropriate weights:
transmits obtained input data to the all neurons on the hidden layer. Input data is the sum of all signals multiplied to appropriate weights:
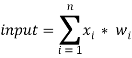
-
Each hidden neuron
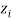 summarizes input signals and applies activation function:
summarizes input signals and applies activation function:
![]()
![]() (1)
(1)
![]() =
= ![]() (2)
(2)
-
Output neuron
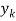 summarizes input signals, afterwards applies activation function. Once activation function is applied, output signal is calculated, which is get as following vector:
summarizes input signals, afterwards applies activation function. Once activation function is applied, output signal is calculated, which is get as following vector:
![]()
![]() (1)
(1)
During the learning of the neural network, each output neuron compares value of the output signal with the target value. Subsequently, error value is determined for each input neuron, which will be used for the weights correction.
Error backpropagation
-
Each output neuron
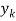 gets target value — correct value, which corresponds to the current input signal and calculates the coefficient of the error:
gets target value — correct value, which corresponds to the current input signal and calculates the coefficient of the error:
![]()
-
Hidden neuron
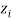 summarizes and calculates values of the error by calculating obtained value to derivative of activation function. Then calculates the value, which describes change of the weight:
summarizes and calculates values of the error by calculating obtained value to derivative of activation function. Then calculates the value, which describes change of the weight:
![]()
![]()
Weights correction
-
Each output neuron
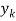 changes the values of its weights with hidden neurons;
changes the values of its weights with hidden neurons;
- Each hidden neuron changes the values of its weights with output neurons.
Condition of work termination of an algorithm can be defined as achievement of total square error of result on the output of network of the minimum preset in advance during training process, and performance of a certain number of iterations of an algorithm.
The choice of initial weights will have an impact on whether the network will manage to reach a local minimum of an error, and how fast this process will happen. Change of weights between two neurons is connected from derivative of activation function of a neuron from the subsequent layer and activation function of a neuron of previous layer. In this regard, it is important to avoid the choice of such initial weights, which will nullify activation function or its derivative. On the other hand, if initial weight are too small, then the entrance signal on the hidden or output neurons will be close to zero that will also lead to very low speed of training.
References:
- Simon O. Haykin, Neural Networks and Learning Machines. — Third Edition, Pearson, 2008. — p. 129–140
- Luis Pedro Coelho, Willi Richert, Building Machine Learning Systems with Python. — Second Edition. — PACKT Publishing, 2015. — p. 65–66







