В этой статье показано, что использование демонстративной модели потребления с функцией полезности Кобба-Дугласа может эндогенно привести к увеличению эластичности по доходу для демонстративного блага и к снижению эластичности по доходу для недемонстративного блага. Новизна работы заключается в том, что здесь подобно изложен математический аппарат, который использовал в своей работе Ори Хеффец.
Ключевые слова: эффект Веблена, эластичность, демонстративный товар.
Начнем с обычной модели потребления. Потребители идентичны во всем, но их доход y является экзогенным фактором. Они максимизируют свои функцию полезности Кобба-Дугласа по двум товарам v и w:
Решение классической задачи теории потребительского выбора:
![]()
![]()
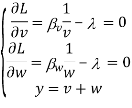
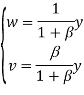
Обозначая через ![]() и
и ![]() верования общества относительно товаров v и w, функция полезности является комбинацией двух категорий: фундаментальной полезности и выводов общества:
верования общества относительно товаров v и w, функция полезности является комбинацией двух категорий: фундаментальной полезности и выводов общества:
![]()
Коэффициент a можно рассматривать как коэффициент чувствительности к мнению общества или социальному статусу. При a = 0 модель сводится к стандартной модели. Что касается информации, мы предполагаем, что товар v демонстративный, а товар w нет, т. е. v наблюдается другими потребителями, а w известен только одному потребителю. С той установкой, что v- видимый товар, а w нет, мнение общества на счет них будет
Тогда новая задача имеет вид:
![]()
![]()
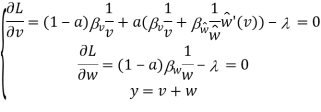
![]()
Полностью разделяющее равновесие требует, чтобы выбор индивидуумов по поводу товара v был оптимальным с учетом ![]() , который они принимают как экзогенный параметр, и чтобы выводы общества были правильны. Чтобы мнение общества было верным необходимо выполнение:
, который они принимают как экзогенный параметр, и чтобы выводы общества были правильны. Чтобы мнение общества было верным необходимо выполнение: ![]() .
.
Учтем ![]() и поделим все на
и поделим все на ![]() :
:
![]() =
=![]()
Чтобы решить полученное ДУ, вводится замена: ![]() , откуда
, откуда ![]() , а также
, а также ![]() .
.
Получили ДУ с разделяющимися переменными: 
Решение дифференциального уравнения:
Применив свойства логарифма, получим: 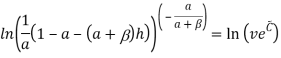
Опускаем логарифм: 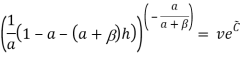
Преобразуем, вернемся к замене и выразим w:
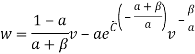
В сочетании с бюджетным ограничением и приняв, что ![]() то так же можно записать получим выражение кривой Энгеля:
то так же можно записать получим выражение кривой Энгеля:
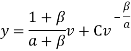
Из полученного уравнения кривой Энгеля возьмем производную y по v:
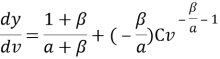
С учетом: ![]() , проведем некоторые преобразования:
, проведем некоторые преобразования:
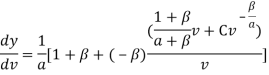
Заметим, что
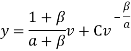 , тогда, поскольку эластичность по определению находится по формуле
, тогда, поскольку эластичность по определению находится по формуле
![]()
Таким образом, математически доказано, что введение социальных сигналов приводит к тому, что при описанной выше постановке, демонстрационный товар становится для потребителя товаром роскоши (![]() > 1), а не демонстрационный товар- товаром первой необходимости (
> 1), а не демонстрационный товар- товаром первой необходимости (![]() <1).
<1).
Литература:
- Ori Heffetz. A Test of Conspicuous Consumption: Visibility and Income Elasticities //The Review of Economics and Statistics, Vol. 93, No. 4 (November 2011), pp. 1101–1117.







