В настоящее время большое внимание уделяется развитию одной из главнейших сфер развития – автомобильной промышленности. Одним из приоритетных направлений которой является совершенствование ходовой части автомобилей, в которой далеко не последнюю роль принимают колеса. Радиус, толщина, рисунок и глубина протектора, все эти факторы призваны обеспечить лучшую сцепляемость автомобиля с дорогой, улучшить управляемость и устойчивость, повысить безопасность. Полномасштабные исследования такого рода, требуют наличия соответствующей аппаратной базы, ведущей к экономическим затратам, которые могут не оправдать полученный результат. Альтернативным вариантом решения является применение компьютерного моделирования, позволяющего значительно сократить сроки создания и анализа исследуемых объектов, снизить экономические затраты и получить необходимые результаты в удобной форме.
На современном рынке для компьютерного моделирования существует множество компьютерных программ, спектр назначения которых охватывает практически всю область человеческой деятельности. Для моделирования физического воздействия на колеса транспортных средств был использован программный комплекс «Универсальный механизм» (UM) [1]. Эта программа широко используется для анализа динамики, напряженно-деформированного состояния и долговечности различных механизмов и машин: металлорежущих станков; подъемно-транспортных машин, автомобилей и железнодорожных экипажей и т.д. Благодаря заложенным в нем математическим закономерностям, UM позволяет рассчитывать компьютерные модели реальных объектов с высокой долей достоверности реальным экспериментальным результатам [2].
В программном комплексе UM c помощью встроенного модуля Automotive была создана компьютерная модель колеса. Модель колеса представляет собой совокупность твердого тела со своими инерционными параметрами и действующих на нее сил. В создании модели не учитывались угол развала/схождения и протекторный профиль колеса.
Была смоделирована типичная ситуация возникающая при повороте транспортного средства – влияния боковой силы, уводящей колесо в сторону в зависимости от вертикальной нагрузки (массы действующей на колесо). В виртуальной компьютерной модели колеса были выставлены физические параметры соответствующие реальным условиям, возникающим при движении автомобиля, т.е. установлен радиус колеса (R13), ширина (12,5 дюйм), масса колеса (5 кг), коэффициенты упругости и жесткости. Вертикальная нагрузка на колесо задавалась через ось вращения.
Результаты моделирования показали, что в идеальных условиях при движении по прямому участку пути, боковые силы, действующие на колесо с обеих сторон, полностью уравновешивают друг друга и никакого отклонения от заданной траектории не происходит. Увеличение скорости вращения и массы (вертикальной нагрузки) так же не приводит к нарушению равновесия. При нарушении идеальных условий, например появлении на дороге препятствий – равновесие нарушается. Причем чем выше скорость, тем сильнее отклонение. При увеличении вертикальной нагрузки наблюдается обратная реакция – чем выше масса, тем меньше отклоняющих сил действует на колесо. Отклонение происходит в сторону меньшего препятствия.
При моделировании движения колеса соответствующей движению по кривому участку пути происходит увеличение действующей боковой силы пропорционально углу отклонения. Причем зависимость носит возрастающий экспоненциальный характер, увеличивающийся пропорционально углу поворота, скорости вращения (движения) и вертикальной нагрузке действующей на колесо.
Рис.1. Боковая сила в зависимости от вертикальной нагрузки на колесо (массы действующей на колесо)
Линия 1- масса 700 кг, 2- масса 1700 кг, 3- масса 1100 кг, 4- масса 2100 кг
На рис. 1 представлена полученная графическая зависимость при угле поворота 10 градусов и скорости вращения колеса, возникающей при движении автомобиля на скорости 40 км/ч. Радиус колеса составляет 32,5 см, что соответствует 13 дюймам. Здесь по оси х – боковая сила уводящая колесо в сторону, по оси у вертикальная нагрузка, действующая на колесо.
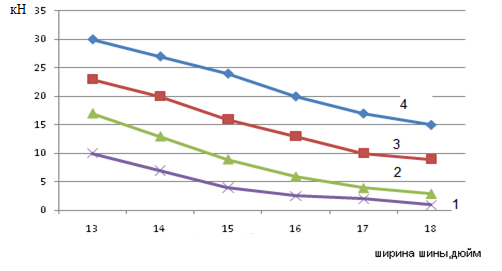
Оценим степень влияния ширины шины на горизонтальную боковую силу (рис.2). Здесь по оси х горизонтальная сила, действующая на колесо, по оси у –ширина шины. Полученный график позволяет наглядно оценить то, что увеличение вертикальной нагрузки на шину, сопровождается увеличением горизонтальной боковой силы, уводящей колесо в сторону противоположную повороту, способствующей появлению эффекта скольжения. При этом проявляются дополнительные горизонтальные силы влияющие на незначительный крен моделируемого колеса. Радиус шины не оказывает сильного воздействия, в отличии от ее ширины, поскольку при увеличении последней горизонтальная боковая сила уменьшается.
Рис.2. Горизонтальная сила в зависимости от ширины шины
На рис.2 линия 1 – масса 700 кг, 2 – масса 1700 кг, 3 – масса 1100 кг, 4 – масса 2100 кг.
Таким образом, использование современных программных комплексов для моделирования различных физических процессов позволяет упростить исследование реальных объектов в тех случаях, когда реальные эксперименты затруднены. Представленные графические зависимости позволяют наглядно оценить степень влияния физических воздействий на колеса транспортных средств.
Литература:
Ковалев Р.В., Даниленко Д.В. Введение в моделирование динамики механических систем. САПР и Графика, № 4, 2008. С. 26-31.