Уравнение движения сыпучего тела в трубе переменного сечения



В статье рассмотрено соотношение усилий при перемещении невесомых шаров в сторону расширения трубы с учетом трения. При перемещении сыпучего тела в сторону расширения трубы частицы среднего слоя под действием силы P и Q раздвигаются при этом крайние частицы приходят к соприкосновению со стенками трубы.

Ключевые слова: сыпучее тело, внутреннее трение, переменное сечение.

Расчет технологического процесса машин, предназначенных для перемещения сыпучих тел (зерна, удобрений и т. п.) сопряжен со значительными трудностями, так как законы движения сыпучих тел изучены еще недостаточно. Обычно сыпучее тело рассматривается как сплошная среда [1]. Однако такое предположение не может правильно характеризовать свойства сыпучего тела при движении, так как в процессе движения происходит взаимной относительное перемещение частиц.

В работе [3] сыпучее тело рассматривается как совокупность отдельных абсолютно твердых частиц, однако исследованный частный случай цилиндрической трубы предполагает отсутствие их относительного перемещения.

Значительно большее теоретическое и практическое значение имеет задача о движении сыпучего тела в трубе переменного сечения, так как такое движение происходит в бункерах, широко применяемых в сельскохозяйственном (да и не только сельскохозяйственном) машиностроении. Предлагаемое исследование выполнено при следующих предположениях:

1) Сыпучее тело состоит из однородных абсолютно твердых шаров, уложенных слоями, перпендикулярными к оси трубы;

2) Укладка шаров слоями сохраняется и в процессе движения;

3) Размеры шаров малы по сравнению с размерами поперечного сечения трубы и высотой столба сыпучего тела;

4) Силы внутреннего трения между шарами и силы трения шаров стенку трубы пропорциональны соответствующим нормальным усилиям;

5) В процессе движения шары вращаются.

Соотношение усилий всмежных слоях без учета веса

Случай абсолютно гладких шаров. Рассмотрим (рис. 1-a,б) равноиение шара 2. На него действуют силы P₁₂, P₃₂ и P₄₂ со стороны окружающих тел как шар абсолютно гладкий.

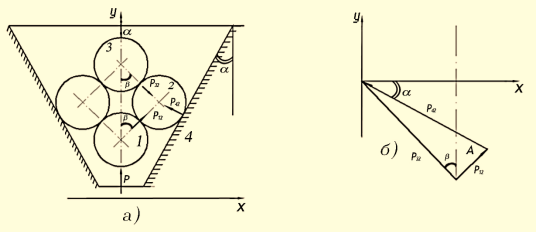
Рис. 1. Схема сил, действующих на абсолютно гладкий невесомый шар, прилегающий к стенке трубы переменного сечения: 1, 2 и 3 — шаровые зерна сыпучего тела; 4 — стенка трубы

Составляем уравнение равновесия шары 2:

Учитывая, что

Получим

(1)

Мы видим, что усилие, приложенное к шару, расположенному в широком сечении, больше, чем к шару, находящемуся в узком сечении.

Если положить, что

До

(2)

На при

Получим

(3)

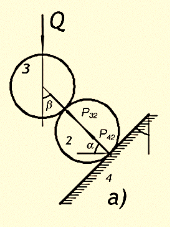
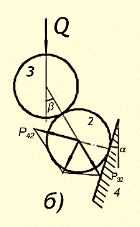
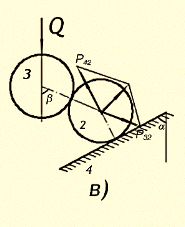
Рис. 2. Влияние углов на движение шара, прилегающего к стенке трубы

Формулы (2) и (3) показывают, что приращение осевого усилия имеет различный вид в зависимости от направления, в котором производится отсчет приращения усилий. Если за исходное взять усилие Р в узком сечении, то приращение усилия при переходе к широкому сечению выражается формулой (2); если же за исходное взять усилие Q в широком сечении, то приращение выражается формулой (3).

При движении в сторону сужения может наступить «самоторможение» абсолютно гладких шаров, когда никакая сила Q>0 не сдвинет сыпучее тело места при P=0. условие самоторможения получим из формулы (1) при P=0

или

(4)

Случай, соответствующий условию (4), изображен на рис. 2, a. если (рис. 2, б), то под действием силы Q происходит выталкивание шара 2 в направлении действия силы Q; в этом случае, очевидно, P>0. Если же (рис. 2, в), то шар 2 будет выталкиваться в направлении, обратном действующей силе , в этом случае сила Р должна изменить свое направление.

При движении абсолютно гладких шаров в сторону расширения трубы самоторможение невозможно. Действительно, полагая в формуле (1) Q=0, так как движущей является сила Р, приходим к выводу, что

или

(5)

Так как углы острые, условие (5) невыполнимо.

Соотношение усилий при перемещении невесомых шаров в сторону сужения трубы с учетом трения. При перемещении сыпучего материала в сторону уменьшения сечения трубы частицы промежуточного слоя, содержащего шар 2, вклиниваются между «ведущим» и «ведомым» слоями, содержащими соответственно шары 3 и 4.

При перемещении частиц должен изменяться в рассматриваемой нами схеме (рис. 1) и угол давления шаров друг на дгуга. Однако ввиду большого числа шаров и беспорядочного их расположения будем считать, что средне статического значение угла для всей массы шаров не изменяется.

При «вклинивании» шара 2 между шарами 1 и 3 силы и отклоняются о нормалей к шарами на угол внутреннего трения в сторону возрастания угла , а сила — на угол внешнего трения частицы о стенку в сторону возрастания . В результате силы и составят с осью трубы углы , а сила составит с нормалью к оси трубы угол (.

По аналогии с формулами (1) и (3) получим

(6)

(7)

За исходные здесь и в дальнейшем принимаем усилие, приложенное к «ведущему» сечению.

Условие самоторможении получим, полагая усилие на <<ведомом>> сечении . из формулы (6) найдем

.(8)

Труба, предназначенная для перемещения сыпучего материала, должна удовлетворять условию соотношению усилий при перемещении невесомых шаров в сторону расширения трубы с учетом трения.

.(9)

Будем считать, что при перемещении сыпучие тела в сторону расширения трубы частицы среднего слоя под действием сил P и Q раздвигаются; при этом крайние частицы приходят в соприкосновение со стенками трубы. Силы и при раздвигании отклоняются от общих нормалей к шарам на угол внутреннего трения в сторону уменьшения углов и составят с осью углы (. Сила отклонится от нормали к стенке трубы по-прежнему на угол в результате чего угол уменьшится на .

Рассуждая аналогично предыдущему по формулам (1) и (2), получим:

(10)

(11)

Условие самоторможения получим, полагая усилие на «ведомом» сечении Тогда

.(12)

Следовательно, самоторможение при движение сыпучего материала в сторону расширения трубы возможно, если выполняется условие (12). При этом обязательно так как ; т. е. самоторможение имеет место в трубах с малым углом расширения и при больших значениях угла трения частиц о стенку трубы. В случае, если труба предназначен для перемещения сыпучих материалов, необходимо выполнение условия

.(13)

Литература:

1. Зенков Р. Л. Механика насыпных грузов. М., Машгиз, 1964. 251 с.
2. Дересевич Г. Механика зернистой среды. Сб. «Проблемы механики». Под редакцией Х. Драйдена и Т. Кармана. — М.: Иностр. лит., 1961. — С. 91–152.
3. Гячев Л. В. О силах, необходимых для перемещения в трубе сыпучего тела. «Механизация и электрификация сельского хозяйства» 1964, № 4, — С. 11–15.