Алгоритм решения задачи порядка горизонтального размещения элементов на печатной плате



При проектировании печатных плат возникает ряд задач, одной из них является задача размещения элементов на печатной плате.

Основной задачей размещения является поиск таких позиций для элементов, чтобы в максимальной мере упростить последующую трассировку связей. Для этого необходимо минимизировать длину связей — размещать элементы, имеющие общие цепи, как можно ближе друг к другу [1].

Целью данной работы является выявление конкретного алгоритма порядка горизонтального размещения элементов на печатной плате.

Алгоритм.

Шаг первый. Обозначения.

Для решения задачи размещения нужно обозначить элементы, выводы элементов, цепи.

Элементы для удобства следует нумеровать с нуля, а выводы и цепи с единицы.

Шаг второй. Составление матрицы отношения элементов и цепей.

После обозначения элементов, выводов и цепей нужно составить матрицу Q размером: количество элементов + 2 × количество цепей + 1.

Первая строка предназначена для нумерации цепей, а первый столбец для нумерации элементов. На пересечении i-той строки, j-того столбца ставится 1, если j-тая цепь принадлежит i-тому элементу, если же данное условие не выполняется, то в ячейке матрицы с индексом ij ставится 0 или не ставится ничего. Последняя строка n предназначена для подсчета суммы единиц в столбце.

Шаг третий. Расчет веса связи элементов, составление матрицы.

Для решения задачи размещения необходимо оценивать связанность элементов между собой. Для такой оценки показателя связанности r_is элемента e_i с элементом e_s нужно рассчитать математическое ожидание — p_j появления ребра полного графа при построении дерева j-той цепи [2].

p_j = (1) [2].

Помимо вероятностного характера соединений между элементами учитывают также различную важность цепей с помощью весовых коэффициентов — w_j, 0j≤1, если все цепи в схеме имеют одинаковую важность, то w_j = 1 [2].

Показатель связанности рассчитывается по формуле:

r_is = (2) [2],

где q_ij и q_sj — элементы матрицы Q.

Смысл этой формулы заключается в следующем: нужно сложить показатели p всех общих цепей элементов i и s, и умножить на w.

После того, как веса связи всех элементов будут посчитаны, нужно составить матрицу R, размерностью n × n, где n — количество элементов. Главная диагональ этой матрицы будет заполнена 0, так ка элемент не может быть связан сам с собой. Остальные ячейки матрицы будут заполнены весами связи элемента i с элементом s.

Шаг четвертый. Размещение элементов.

Нужно выбрать неперемещаемый элемент (обычно это e₀) он будет установлен в начале печатной платы. Далее по матрице R определяется элемент, который имеет наибольший вес связи с элементом, уже установленным на печатной плате, такой элемент устанавливается следующим. Затем на плату помещается элемент, имеющий наибольший СУММАРНЫЙ вес связи с уже размещенными элементами (для элемента e_s: r=r_0s+r_is, если элементы e₀ и e_i уже размещены), и так далее пока все элементы не будут размещены.

Пример. Определить очередность расположения элементов на данной печатной плате.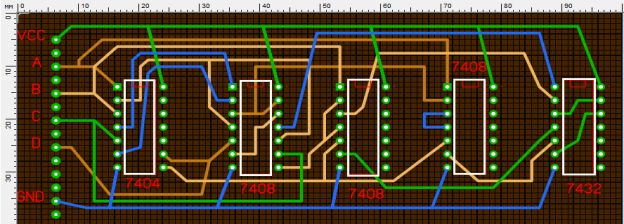Рис. 1. Пример задачи размещения.

Решение будет осуществляться с помощью вышеприведенного алгоритма.

1.

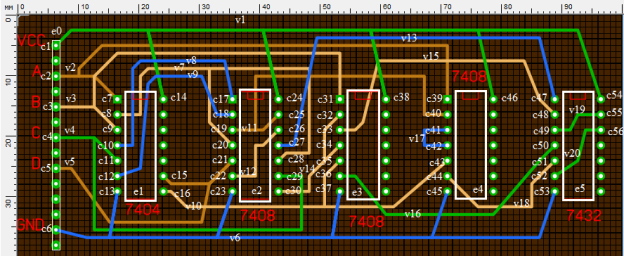
Рис 2. Пример обозначения элементов, цепей, выводов элементов.

2.

Таблица 1

Пример матрицы Q

VE	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
0	1	1	1	1	1	1
1	1	1	1	1	1	1	1	1	1	1
2	1			1	1	1	1	1	1		1	1	1	1
3	1		1			1				1				1	1	1
4	1	1				1				1	1						1	1
5	1					1							1		1	1		1	1	1
nS	6	3	3	3	3	6	2	2	2	3	2	1	2	2	2	2	1	2	1	1

3.

n1=n6=6; n2=n3=n4=n5=n10=3; n7=n8=n9=n11=n13=n14=n15=n16=n18=2;

n12=n17=n19=n20=1.

p1=p6=1/3; p2=p3=p4=p5=p10=2/3; p7=p8=p9=p11=p13=p14=p15=p16=p18=1;

p12=p17=p19=p20=2.

Таблица 2

Пример матрицы R

		e
		0	1	2	3	4	5
e	0	0	10/3	6/3	4/3	4/3	2/3
	1	10/3	0	15/3	6/3	6/3	2/3
	2	6/3	15/3	0	5/3	5/3	5/3
	3	4/3	6/3	5/3	0	4/3	8/3
	4	4/3	6/3	5/3	4/3	0	5/3
	5	2/3	2/3	5/3	8/3	5/3	0

4. Элементы будут располагаться в следующем порядке e₀, e₁, e₂, e₃, e_4, e₅. То есть начальное расположение элементов было верным.

Вывод. В ходе данной работы был предложен алгоритм решения задачи горизонтального размещения элементов на печатной плате; приведен конкретный пример. Данный алгоритм может быть использован как при проектировании печатной платы, так и при решении других задач оптимального размещения связанных элементов. Вышеприведенный алгоритм также может быть использован в программах автоматизированного проектирования печатных плат на ЭВМ.

Литература:

1. Муханов В. В., Серегин А. В. Конструкторское проектирование. // URL: http://window.edu.ru/resource/668/28668/files/ustu275.pdf (Дата обращения: 25.01.2019)
2. Виноградов М. В. Оптимизация компоновки и размещения элементов на печатных платах.