Библиографическое описание:
Гасанов, И. Р. Об определении зависимости между временем релаксации и гидравлическим сопротивлением при фильтрации в пласте неравновесной жидкости / И. Р. Гасанов. — Текст : непосредственный // Молодой ученый. — 2019. — № 5 (243). — С. 19-21. — URL: https://moluch.ru/archive/243/56119/ (дата обращения: 23.04.2025).
В работе выводятся формулы для определения времени релаксации в зависимости от гидравлического сопротивления 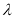 и параметра Щелкачева
и параметра Щелкачева 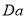 [1, 2, 3].
[1, 2, 3].
Ключевые слова: гидравлическое сопротивление, число Рейнолдса, трехчленный закон фильтрации, время релаксации
The paper derives formulas for determining the relaxation time depending on the hydraulic resistance and the Schelkachev parameter 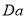 [1, 2, 3].
[1, 2, 3].
Keywords: hydraulic resistance, Reynolds number, three-term filtration law, relaxation time
Как известно, в наиболее общем случае закон фильтрации можно представить в виде [1]:
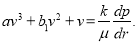 (1)
(1)
Здесь 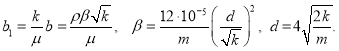
Использование кубического слагаемого в уравнении (1) связано с необходимостью, с одной стороны, увеличения точности, с другой — для учета неравновесных свойств фильтрационного потока и влияния инерционных сил. Как видно, при 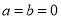 из формулы (1) получается закон Дарси. При
из формулы (1) получается закон Дарси. При 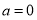 получается двучленный закон Форхгеймера. Для получения нужной формулы применим следующие выражения:
получается двучленный закон Форхгеймера. Для получения нужной формулы применим следующие выражения:
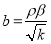 , (2)
, (2)
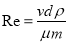
, (3)
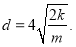 (4)
(4)
Из (3) и (4) получается:
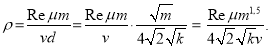 (5)
(5)
Если учесть (5) в (2) получается:
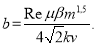 (6)
(6)
А теперь представим формулу (1) в следующем виде:
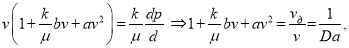
где 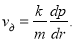 (7)
(7)
С другой стороны, из выражения
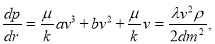 (8)
(8)
с учетом (7) и (8) получается:
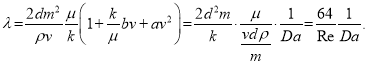 (9)
(9)
Так же из (7) и (6) получается:
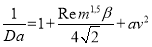 или
или
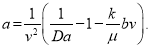 (10)
(10)
При 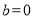 имеем
имеем 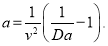 (11)
(11)
Для определения времени релаксации при фильтрации неравновесной жидкости используем формулу:
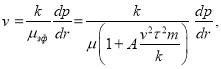 (12)
(12)
откуда получается 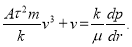 (13)
(13)
Если формулу (13) сравнить с формулой (1) при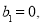 то получаем:
то получаем:
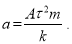 (14)
(14)
Если формулу (14) учесть в (11), то получаем:
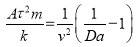
или
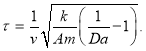 (15)
(15)
Если 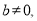 то получается:
то получается:
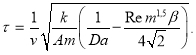 (16)
(16)
Из (9) 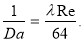
Если учесть последнее в (15), то получаем:
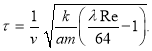 (17)
(17)
Таким образом, мы получили зависимость между временем релаксации и гидравлическим сопротивлением при фильтрации в пласте неравновесной жидкости.
Литература:
-
Гасанов И. Р. Обобщенная формула Дюпюи // Международный журнал: Молодой ученый. — № 15 (149). — Апрель 2017.
-
Гасанов И. Р. К вопросу определения гидравлического сопротивления при двучленном законе фильтрации углеводородов в пористой среде с учетом влияния начального градиента // Международный журнал: Молодой ученый. — № 49 (235). — Декабрь 2018.
-
Гасанов И. Р. Об определении гидравлического сопротивления при турбулентном режиме фильтрации флюида в пористой среде // Международный журнал: Молодой ученый. — № 2 (240). — Январь 2019.
Основные термины (генерируются автоматически): время релаксации, гидравлическое сопротивление, неравновесная жидкость, формула.
Ключевые слова
гидравлическое сопротивление,
время релаксации,
число Рейнолдса,
трехчленный закон фильтрации
Похожие статьи
В данной работе делается попытка определения числа Рейнольдса и гидравлического сопротивления при двучленном законе фильтрации углеводородов в пористой среде с учетом влияния начального градиента, а также получена формула скорости в зависимости от эт...
В данной работе рассматривается прямолинейно-параллельный неустановившийся фильтрационный поток упругой жидкости, при второй фазе распределения давления в пласте. Задача решается методом усреднений.
В работе предлагается метод, по которому можно более простым способом решать гидродинамические задачи, связанные с неустановившейся фильтрацией упругой жидкости в пористой среде с учетом влияния начального градиента.
В данной работе делается попытка определения числа Рейнольдса и гидравлического сопротивления при двучленном законе фильтрации углеводородов в пористой среде с учетом влияния начального градиента, а также получена формула скорости в зависимости от эт...
В статье рассматривается приближенный метод решения задачи теории упругого режима для одномерного поступательного движения жидкости с предельным градиентом давления для второй фазы. Задача решена методом «усреднений».
В статье рассматривается прямолинейно-параллельный неустановившийся фильтрационный поток упругой жидкости, при заданном забойном давлении во времени. Задача решается методом усреднений [1, 2].
В статье закон фильтрации берется в более общем виде. Для этого в формуле от нужно использовать кубическое слагаемое. При этом увеличивается точность при обработке индикаторных линий. Однако это необходимо также и для учета неравновесных свойств ...
В статье выведены формулы для определения коэффициента гидравлического сопротивления при двухфазной фильтрации, а так же для безразмерной функции Леверетта в пластовых условиях.
В статье предложены формулы для определения градиента давления или депрессии (который должен быть дополнительно преодолен и связан с увеличением скорости фильтрации).
Определение гидравлического сопротивления при фильтрации жидкости в пористой среде имеет большое значение.
В данной статье определяется гидравлическое сопротивление при двучленном законе фильтрации жидкости в пористой среде.
![]() и параметра Щелкачева
и параметра Щелкачева ![]() [1, 2, 3].
[1, 2, 3].
![]() [1, 2, 3].
[1, 2, 3].
![]() (1)
(1)
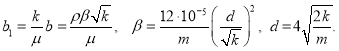
![]() из формулы (1) получается закон Дарси. При
из формулы (1) получается закон Дарси. При ![]() получается двучленный закон Форхгеймера. Для получения нужной формулы применим следующие выражения:
получается двучленный закон Форхгеймера. Для получения нужной формулы применим следующие выражения:
![]() , (2)
, (2)
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
![]()
![]() (7)
(7)
![]() (8)
(8)
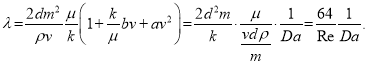 (9)
(9)
![]() или
или
![]() (10)
(10)
![]() имеем
имеем ![]() (11)
(11)
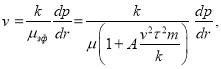 (12)
(12)
![]() (13)
(13)
![]() то получаем:
то получаем:
![]() (14)
(14)
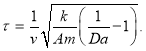 (15)
(15)
![]() то получается:
то получается:
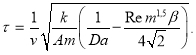 (16)
(16)
![]()
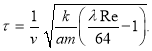 (17)
(17)







