Для описания поведения реального газа различными авторами было предложено более 150 уравнений. Наиболее известным является уравнение Ван-дер-Ваальса. Решения большинства уравнений и расчеты по ним требуют вычислительного эксперимента и подбора большого количества констант. Так, для уравнения Камерлинг-Оннеса требуется подбор 25 констант. Но во многих случаях можно воспользоваться уравнением идеального газа, позволяющего проводить простые расчеты. В связи с этим актуальным является вопрос исследования газа Ван-дер-Ваальса с помощью численного моделирования.
В последнее время численное моделирование все чаще называют вычислительным экспериментом, поскольку оно имеет много общего с лабораторными экспериментами [1, 2]. Основные этапы реального эксперимента (создание установки и измерения) заменяются математической моделью и проведение расчетов. Этап обработки данных остается без изменений.
- Приведенное уравнение Ван-дер-Ваальса
Для исследования свойств газа Ван-дер-Ваальса методом вычислительного эксперимента удобно представить уравнение Ван-дер-Ваальса в виде, не зависящем от параметров конкретного газа [3, 4]. Такое представление существует и носит название приведенного уравнения Ван-дер-Ваальса.
Примем в качестве единиц объема, давления и температуры критические значения этих величин. Объем, давление и температура, измеренные в таких единицах, называются приведенными. Они определяются выражениями:
|
|
(1) |
Уравнение состояния, записанное в этих безразмерных переменных, называется приведенным уравнением состояния.
Критические параметры вещества были выражены через постоянные Ван-дер-Ваальса [4]:
|
|
(2) |
Из (1) и (2) получаем
![]() ,
, ![]() ,
, ![]() .
.
Подставляя эти выражения в уравнение Ван-дер-Ваальса
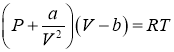 ,
,
получим:
|
|
(3) |
Полученное выражение (3) и есть приведенное уравнение Ван-дер-Ваальса. Оно не содержит постоянных, зависящих от природы вещества. Другими словами, если измерять давление, объем и температуру в единицах их критических значений, то уравнение состояния становится одинаковым для всех веществ. Это положение называется закономсоответственных состояний (соответственными называются такие состояния разных веществ, которые имеют одинаковые значения приведенных параметров ![]() ). Из него, в частности, следует, что если две из приведенных переменных
). Из него, в частности, следует, что если две из приведенных переменных ![]() для разных веществ совпадают, то третья переменная также совпадает, и состояния этих веществ будут соответственными.
для разных веществ совпадают, то третья переменная также совпадает, и состояния этих веществ будут соответственными.
Вещества, подчиняющиеся закону соответственных состояний и удовлетворяющие одному и тому же приведенному уравнению состояния, называются термодинамически подобными веществами. Термодинамическое подобие позволяет делать выводы о свойствах одного вещества, если известны свойства другого (принцип термодинамического подобия) [5–7].
Следует отметить, что закон соответственных состояний имеет приближенный характер. Тем не менее, с его помощью можно получать вполне пригодные для оценок результаты. Отметим также, что этот закон не связан с конкретным видом уравнения состояния, а является следствием лишь того обстоятельства, что в это уравнение входят всего две постоянные ![]() и
и ![]() . Другое уравнение состояния с двумя параметрами тоже привело бы к закону соответственных состояний.
. Другое уравнение состояния с двумя параметрами тоже привело бы к закону соответственных состояний.
Приведенное уравнение позволяет более точно указать критерии, при которых уравнение состояния идеального газа может быть хорошим приближением к действительности. Покажем, что для этого необходимо, чтобы объем газа был велик по сравнению с его критическим объемом.
В случае, когда 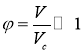 приведенное уравнение (3) можно записать в виде:
приведенное уравнение (3) можно записать в виде:
|
|
(4) |
Для газа Ван-дер-Ваальса [4] критический коэффициент равен 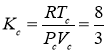 . Подставляя выражение
. Подставляя выражение ![]() в уравнение (4), получим:
в уравнение (4), получим: 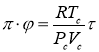 , или, с учетом определения приведенных величин,
, или, с учетом определения приведенных величин, 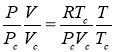 , и, следовательно,
, и, следовательно, ![]() , т. е. уравнение состояния идеального газа.
, т. е. уравнение состояния идеального газа.
- Построение изотермы газа Ван-дер-Ваальса
Вычислительный эксперимент выполнен в системе Mathematica. Суть программирования состоит в том, чтобы создать комбинацию встроенных функций, соответствующую алгоритму. Считается, что Mathematica входит в тройку лидеров среди систем компьютерной математики [8–9].
Для построения изотермы газа Ван-дер-Ваальса в системе Mathematica вначале необходимо создать функцию зависимости давления от температуры и объема. Согласно приведенному уравнению Ван-дер-Ваальса (3) эта функция имеет вид:
|
|
(5) |
Затем, с помощью оператора построения двухмерных графиков Plotможно строить график этой функции при постоянной температуре, задавая желаемые параметры форматирования.
Код программы для построения изотермы при ![]() приведен на рис. 1. Отметим, что величина
приведен на рис. 1. Отметим, что величина ![]() выбрана произвольно. В элементы форматирования входят задание диапазонов графика по горизонтальной и вертикальной осям, подписей по осям и величины шрифта для них, выбор положения вертикальной оси, размер шрифта меток на осях, цвет и толщина линии графика. Результат выполнения этой программы (изотерма) приведен на рис. 2.
выбрана произвольно. В элементы форматирования входят задание диапазонов графика по горизонтальной и вертикальной осям, подписей по осям и величины шрифта для них, выбор положения вертикальной оси, размер шрифта меток на осях, цвет и толщина линии графика. Результат выполнения этой программы (изотерма) приведен на рис. 2.

Рис. 1. Код программы построения изотермы Ван-дер-Ваальса вместе с изотермой идеального газа
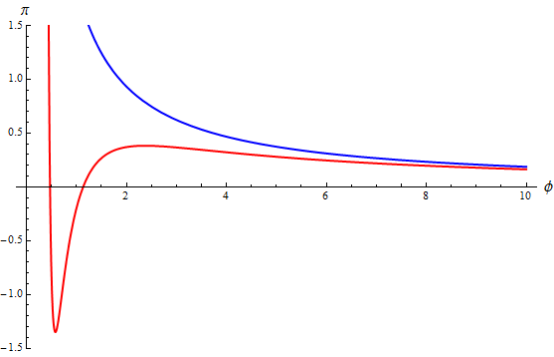
Рис. 2. Изотермы газа Ван-дер-Ваальса и идеального газа при ![]() .
.
Интересно сравнить изотерму газа Ван-дер-Ваальса с изотермой идеального газа при той же температуре. Согласно (4) приведенное уравнение идеального газа имеет вид ![]() . Отсюда получаем функцию зависимости давления от объема и температуры:
. Отсюда получаем функцию зависимости давления от объема и температуры: 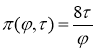 .
.
Как и в предыдущем случае, необходимо создать функцию, соответствующую этой зависимости. Код программы приведен на рис. 3 и полученный результат ее работы — на рис. 4. Как видно из рис. 4, при больших величинах приведенного объема уравнение состояния идеального газа дает те же результаты, что и уравнение Ван-дер-Ваальса.

Рис. 3. Код программы построения графика расхождения изотерм.
Выводы
В среде компьютерной математики Mathematica были исследованы свойства газа Ван-дер-Ваальса. В основу математической модели было положено приведенное уравнение Ван-дер-Ваальса 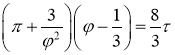 , ввиду его универсальности, т. е. одинаковости уравнения для всех веществ.
, ввиду его универсальности, т. е. одинаковости уравнения для всех веществ.
Построены изотерма Ван-дер-Ваальса и изотерма идеального газа, а также график расхождения изотерм идеального газа и Ван-дер-Ваальса.
В дальнейшем планируем определить условия применимости уравнения идеального газа Ван-дер-Ваальса для описания реального газа.
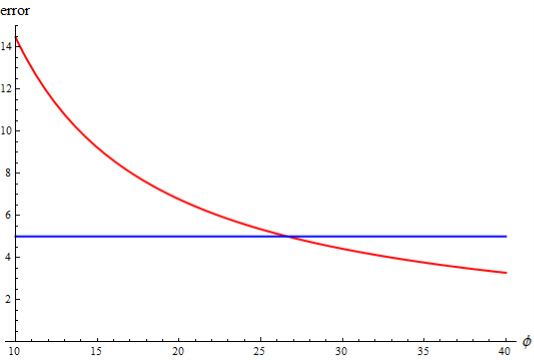
Рис. 4. Зависимость ошибки для уравнения идеального газа от объема при температуре ![]() .
.
Литература:
- Гулд Х., Тобочник Я. Компьютерное моделирование в физике: В 2-х частях. Часть 1.– М.: Мир,1990 -349 с.
- Гулд Х., Тобочник Я. Компьютерное моделирование в физике: В 2-х частях. Часть 2.– М.: Мир,1990 -400 с.
- Савельев И. В. Курс общей физики, том.1. — М.: Наука, 1970. — 511 с.
- Ландау Л. Д., Лифшиц Е. М. Курс общей физики. Механика и молекулярная физика. — М.: Наука, 1965. — 384 с.
- Сивухин Д. В. Общий курс физики. Термодинамика и молекулярная физика. — М.: Наука, 1979. — 543 с.
- Ферми Э. Термодинамика. — Изд-во Харьковского университета, 1973.- 136 с.
- Базаров И. П. Термодинамика. — М.: Высш.шк.,1991. — 376 с.
- Половко А. М. Mathematica для студента. — СПб.: БХВ-Петербург, 2007. — 368 с.
- Дьяконов В. П. Mathematica 5.1/5.2/6. Программирование и математические вычисления. — М.: ДМК-Пресс, 2008. — 576 с.







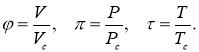
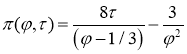 .
.
