В работе дается методика, по которой можно определить критическое значение числа Рейнольдса, т. е. значение 
, при котором происходит переход от ламинарного режима фильтрации в пласте углеводородов к турбулентному [1, 2, 3].
Ключевые слова: число Рейнольдса, критическое значение, метод установившихся отборов, инерционные силы, скорость.
The paper gives a technique by which one can determine the critical value of the Reynolds number, i.e. the value , at which the transition from laminar filtration in the reservoir of hydrocarbons to turbulent occurs [1, 2, 3].
Keywords. Reynolds number, critical value, steady-state selection method, inertial forces, speed.
Как известно [1, 2], для определения притока флюида к одиночной скважине с учетом влияния изменения физических свойств флюида и коллектора принимается, что зависимость комплекса параметров от депрессии можно в наиболее общем случае аппроксимировать многочленом степени 
т. е.
(1)
где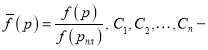 
коэффициенты, характеризующие изменение комплекса параметров флюида и коллектора в зависимости от снижения давления и сопутствующих ему процессов. Следует отметить, что для однофазной нефти
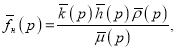
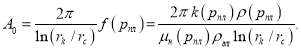(2)
Для жидкой фазы газированной нефти
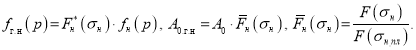(3)
Здесь 
соответственно текущее давление и насыщенность коллектора флюидом в произвольной точке пласта; 
коэффициент продуктивности скважины; 
соответственно абсолютная и фазовая проницаемость и действующая толщина пласта; 
вязкость и плотность флюида.
При этом дебит нефти определяется формулой:
(4)
Обычно изменения комплекса параметров происходят по квадратичному закону, т. е.
Тогда 
или
(5)
Здесь 
Пусть 
Тогда формула (5) примет привычный вид кубической функции
(6)
Здесь 
Для функции 
критические области находятся из условий
Тогда получаем:
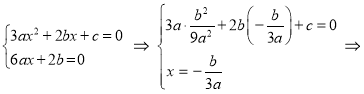
Как известно, для кубического уравнения при изменении знака 
от 
вид графика кубической функции также меняется. На рис. 1 показаны графики функции 
при различных знаках 
Это связано с тем, что с увеличением депрессии увеличивается скорость, и под влиянием инерционных сил ламинарный режим фильтрации переходит на турбулентный. В этом случае процесс от устойчивого состояния при 
переходит на неустойчивый при 
[3]. В связи с чем и график функции, описывающий это состояние, меняет свой вид (см.рис.1).
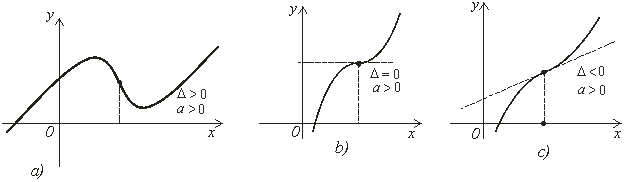
Рис. 1.
Таким образом, для определения 
проводятся исследования методом установившихся отборов, и для нескольких значений 
определяются значения q. Обычно влияние инерционных сил происходит при больших значениях депрессии 
Начиная с третьей точки по предлагаемой методике определяются значения а и b. Для каждой новой точки вид кривой, а следовательно — и значения а и b меняются. Значения а и b определяются или по методу наименьших квадратов или по методике [2].
Для этого координаты функции 
перестраивают следующим образом:
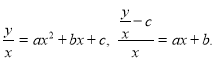Построив график 
от х находим по точке пересечения прямой с осью Оy, значения b и по углу наклона прямой к оси Ох значения 
Здесь
Таким образом, проводятся исследования методом установившихся отборов. Строится зависимость между 
Для каждой следующей точки по предложенной методике определяются значения 
и 
Там, где знак 
становится отрицательным и происходит переход от ламинарного режима к турбулентному, а если знак не изменяется, значит, режим фильтрации остается ламинарным. В пласте 
определяется по формуле 
где v — скорость фильтрации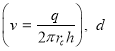 
– эффективный диаметр (
где k — абсолютная проницаемость, m — пористость), 
— плотность нефти, 
— вязкость нефти.
Литература:
- Временное руководство по гидродинамическим методам изучения фильтрационных свойств залежей нефти и газа, характеризующихся высокими пластовыми давлениями /М. Т. Абасов, Э. Х. Азимов, А. М. Кудиев, Г. С. Мамиев и др. –Баку: Элм, 1978. –128 с.
- Э. Х. Азимов, В. Н. Аддахвердиев, Л. М. Билаллы, И. Р. Гасанов. Методика интерпретации индикаторных линий газовых и газоконденсатных скважин //Азербайджанское нефтяное хозяйство. — 1987. — № 25. — С.24–28.
- Мирзаджанзаде А. Х., Ширинзаде С. А. Повышение эффективности и качества бурения глубоких скважин. — М.: Недра, 1986. — 278 с.
