В работе приведены методические рекомендации учителям математики, по изучению элементов теории графов на факультативных занятиях в рамках основного общего образования.
Ключевые слова: теория графов, факультативные занятия, основная школа, методические рекомендации.
В школьном курсе математики ученикам часто не хватает интересных и занимательных задач. Задачи теории графов способны заинтересовать учащихся. Однако учителя редко рассматривают вопросы теории графов, из-за отсутствия методики их использования. В статье предпринята попытка сформулировать методические рекомендации для учителей, которые хотели бы изучать элементы теории графов во внеурочной работе.
На первом занятии факультативного курса рекомендуется рассмотреть примеры задач, приводящих к графам, историю возникновения теории графов и ее применение в различных сферах деятельности. Составленные задачи должны подводить учащихся к мысли о том, что их решение имеет некоторое сходство между собой благодаря использованию схожих рисунков и схем.
Следующие занятия стоит посвятить изучению основных понятий теории графов, а также рассмотреть способы задания графов. В результате, учащиеся должны научиться строить графы согласно заданным условиям.
Введение леммы о рукопожатиях рекомендуем начать с решения задачи: «Пять человек при встрече обменялись рукопожатиями (каждый пожал руку каждому по одному разу). Сколько рукопожатий было сделано?». Данная задача подводит к введению леммы и ее решение не вызывает затруднений. Затем необходимо рассмотреть более сложную задачу, требующую непосредственного доказательства. После ее решения можно сформулировать следствия леммы. В закреплении материала стоит рассмотреть задачи на применение леммы, а также другие занимательные задачи теории графов.
На следующих занятиях можно перейти к рассмотрению некоторых видов графов: полный и пустой граф, дополнение графа и подграф. Все понятия следует сопровождать рассмотрением конкретных примеров. Продолжить изучение видов графов можно введением понятий: путь, цикл, связный граф и компонента связности графа.
Решение задач, в которых требуется найти кратчайший путь, способствует формированию представления о пути в графе. Обратим внимание на введение понятия «компонента связности». Подходя к ее определению, необходимо сказать, что даже если между какими-то двумя вершинами нет пути, это может быть один граф, а не несколько. В качестве наглядного примера, можно рассмотреть остров Сахалин, который является частью России, но не имеет автомобильного моста, соединяющего остров с материковой частью страны. Можно предложить ребятам привести свои примеры компонент связности.
Завершить изучение видов графов, можно рассмотрением темы «Деревья». Прежде чем вводить данное понятие, учитель, в качестве домашнего задания, может попросить учеников нарисовать генеалогическое древо своей семьи. Прием направлен на актуализацию знаний учащихся. Помимо понятия графа-дерева, можно ввести определения таких понятий как остов графа, лес и рассмотреть доказательство теоремы о количестве ребер дерева. Закрепить изученный материал можно выполнением заданий на построение деревьев и решение более сложных задач, с применением деревьев.
Проведение обобщающей игры по пройденным разделам, будет способствовать лучшему усвоению материала.
Также рекомендуется посвятить пару занятий вопросам изображения графов. В начале от учителя требуется познакомить учащихся с геометрическими особенностями изображения графов, ввести понятия плоского и изоморфного графов, сформировать навык задания плоских графов различными способами. В качестве актуализации знаний учащимся можно предложить определить, являются ли представленные на рисунке графы изображением одного и того же графа или нет:
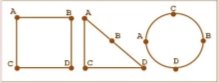
Выводы, которые должны сделать учащиеся по этой теме, заключаются в том, что один и тот граф можно изобразить по-разному, и плоские графы — это такие графы, рёбра которых на рисунке не пересекаются.
Также стоит рассмотреть формулу Эйлера. Подведением к данному вопросу будет служить задача о трех колодцах. Необходимо обратить внимание обучающихся на тот факт, что при решении задач на определение числа граней в графе, формула Эйлера в том виде, в котором она дана: В — Р + Г = 2, подразумевает подсчет и внешней грани.
Следующее занятие должно рассматривать вопросы, связанные с понятием двудольности графа. Здесь, не лишним будет вспомнить содержание предыдущего урока, а именно задачу о трех колодцах. Можно сказать учащимся, что граф, который использовался в данной задаче, является полным двудольным графом, и так как задача была не разрешима, это означает, что графы такого рода не могут быть плоскими.
На одном из занятий можно рассмотреть тему: «Задачи на раскраску». Для актуализации знаний можно рассмотреть политическую карту мира (не раскрашенную в цвета) и попросить учащихся раскрасить ее в такое наименьшее количество цветов, которого будет достаточно для того, чтобы соседние страны имели разные цвета. Это задание подведет учащихся к основному вопросу урока, а именно, к задаче о четырех красках. Затем вводятся основные понятия и положения темы, а также исторические сведения о возникновении проблемы 4-х красок.
Изучение темы «Эйлеровы графы», можно начать с задания: «нарисовать «домик» и прямоугольник с диагоналями, не отрывая карандаш от бумаги». Учащиеся должны понять, что «домик» возможно нарисовать, не отрывая карандаш от бумаги, а «прямоугольник» — нет. При формировании новых знаний по теме, можно привести в пример решение исторической задачи о кёнигсбергских мостах. Перед рассмотрением текстовых задач необходимо ввести алгоритм решения задач для эйлеровых графов. В конце занятия решаются задачи на построение уникурсальных линий. В качестве занимательного материала можно изучить с обучающимися задачи известного писателя Льюиса Кэрролла.
Также для общего развития учащихся, можно ввести задачи на прохождение лабиринтов. Рассмотрение темы можно начать с исторической фабулы, рассказав учащимся легенду о минотавре, жившем в лабиринте. Далее изучается теоретическая сторона вопроса. В качестве закрепления новых знаний учащиеся проходят лабиринты и решают задачи на графы. В конце занятия проводится проверочная работа по всему материалу курса, и выдаются темы рефератов и докладов для последнего занятия курса.
На итоговом занятии выполняется защита докладов учеников. Примерные темы докладов должны расширять вопросы, которые были изучены в курсе.
Использование графов в качестве некоторого вспомогательного средства позволяет облегчить процесс обучения и подготовить учеников к восприятию сложных тем в курсе школьной математики. Применение теории графов на факультативных занятиях по математике позволяет упростить решение многих математических задач и доказательств, придает им наглядность и простоту. Также, задачи на графы можно использовать при подготовке к олимпиадам для развития сообразительности учеников. Изучение теории графов повышает качество обучения на уроках математики, алгебры, геометрии и информатики и способствует развитию логического мышления обучающихся.







