В рамках данной статьи предложена корреляционно-регрессионная модель для оценки стоимости жилой квартиры. Для исследования был изучен рынок вторичного жилья города Хабаровска. Зависимость цены квартиры от ряда факторов строится на основе уравнения регрессии. Функциональная зависимость между двумя переменными означает, что каждому значению одной переменной соответствует вполне определенное значение другой. Если зависимость между двумя величинами такова, что каждому значению одной из них соответствует определенное среднее значение другой, то такая зависимость называется корреляционной. Корреляционная зависимость между двумя переменными – это функциональная зависимость между одной переменной и ожидаемым (условным средним) значением другой. Уравнение такой зависимости между двумя переменными называется уравнением регрессии. В случае если переменных две (одна зависимая и одна независимая), то регрессия называется простой, а если их более двух, то множественная.
Модель такой зависимости может быть представлена в виде:
y = α + βx + ε,
где у – зависимая переменная (результативный признак); х – независимая переменная (факторный признак); α – свободный член уравнения регрессии; β – коэффициент уравнения регрессии; ε – случайная величина, характеризующая отклонения фактических значений зависимой переменной у от модельных или теоретических значений, рассчитанных по уравнению регрессии.
Одним из обязательных этапов любого исследования является статистический анализ данных. Работа состоит из нескольких этапов. Во-первых, это составление выборки и подбор возможных факторов, влияющих на стоимость жилья. Для построения эконометрической модели было проведено обследование вторичного рынка жилья города Хабаровска. Для моделирования составили выборку [1] двухкомнатных квартир общим количеством в 500 наблюдений (по 100 квартир каждого района г. Хабаровска: Железнодорожного, Индустриального, Кировского, Краснофлотского и Центрального). Результирующим фактором модели выбрали стоимость квартиры. В качестве регрессоров выступали следующие факторы:
месторасположение (пять районов);
этаж (первый/последний или средний);
тип здания (панельный дом или кирпичный);
планировка (новая, хрущевка, индивидуальная, улучшенная, брежневка);
площадь (общая площадь квартиры и площадь кухни);
санузел (раздельный или совмещен);
наличие балкона/лоджии;
наличие телефона;
состояние квартиры (состояние отличное, хорошее, удовлетворительное, нормальное, евроремонт).
В данном случае, для построения модели необходимо, чтобы в качестве объясняющих переменных выступали как численные величины, так и качественные переменные. Обычно в роли таких переменных выступают дихотомические или, по-другому, бинарные переменные или фиктивные, которые могут принимать только два значения, обычно это 0 и 1 (есть признак или его нет). Они позволяют отслеживать структурные изменения в анализируемых явлениях или процессах. При этом необходимо иметь в виду, что количество таких переменных должно быть на единицу меньше, чем число уровней изучаемого признака. Таким образом, в модель будут введены только две количественные переменные – общая площадь и площадь кухни. Остальные же параметры (местоположение, планировка, состояние квартиры, наличие лоджии и т. д.) отражают качественные характеристики, поэтому они будут являться фиктивными и принимать значения 0 или 1. При этом один из параметров берется за базу и в уравнение не включается. В данной модели за базу были приняты такие параметры как: Индустриальный район, панельный дом, совместный с/у, квартира без балкона, без телефона, улучшенная планировка и состояние квартиры, требующее косметического ремонта.
Затем проводим спецификацию модели: отбор факторов (проверка на мультиколлинеарность; проверка на значимость); выбор формы модели.
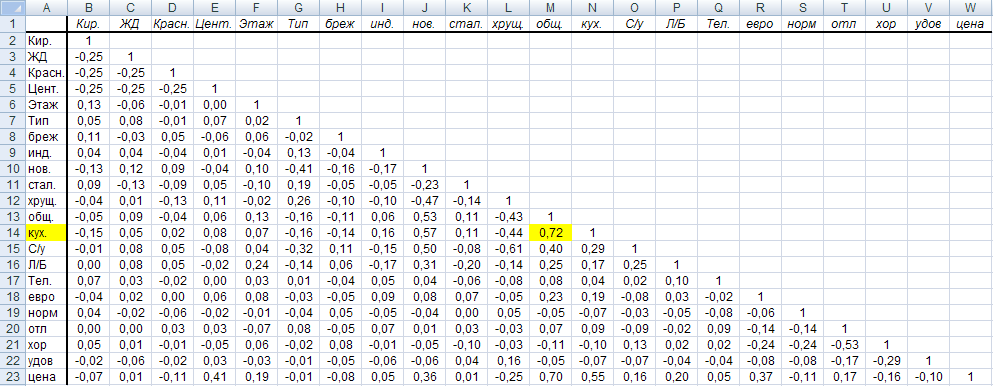
Чтобы отобрать факторы для построения уравнения регрессии, необходимо проверить имеющиеся на мультиколлинеарность. Мультиколлинеарность – тесная корреляционная взаимосвязь между отбираемыми для анализа факторами, совместно воздействующими на общий результат, которая затрудняет оценивание регрессионных параметров. Мультиколлинеарность не позволяет однозначно определить коэффициенты уравнения регрессии и разделить вклады объясняющих переменных в их влиянии на зависимую переменную. В этом случае невозможно сделать обоснованные статистические выводы об этих коэффициентах. Для проверки факторов на мультиколлинеарность построили корреляционную матрицу (таблица, где по горизонтали и вертикали расположены все факторы, а остальное пространство заполнено коэффициентами корреляций между соответствующими факторами).
Рисунок 1. Корреляционная матрица.
В соответствии с полученными результатами, можно сказать, что мультиколлинеарность присутствует. Такие факторы в модели как общая площадь и площадь квартиры зависят друг от друга, между ними наблюдается высокая коррелированность. Поэтому мы исключаем из модели такой фактор как площадь кухни.
Исключив площадь кухни, мы избавились от мультиколлинеарности, это позволяет построить линейную регрессионную модель. По значению p – величины (она должна быть < 0,05) и t – статистики (должно быть > 2) определяется незначимый фактор, у которого p – value максимальное и больше 0,05. Затем, удаляем этот фактор и сравниваем скорректированный коэффициент детерминации исходной модели и вновь полученной. Если коэффициент детерминации при удалении фактора увеличивается, то значит, что удаленный фактор незначим. Подобную процедуру повторяем до тех пор, пока не увидим, что коэффициент детерминации стал уменьшаться. В результате ряда итераций получили, что не значимыми оказались такие факторы, как: наличие балкона, новая планировка, планировка брежневка, нормальное состояние и удовлетворительное состояние. Можно сделать вывод, что на стоимость квартиры влияют в равной степени «новая планировка» и «планировка брежневка», нормальное и удовлетворительное состояния квартиры; значимого влияния на стоимость квартиры не оказывает наличие или отсутствие балкона. Дисперсионный анализ итоговой регрессии показывает, что уравнение регрессии значимо (оцениваем по p – величине статистики Фишера, которая должна быть меньше 0,05).
Итоговое уравнение регрессии примет вид:
Цена = - 996,899 +65,5403 ×общ. площадь +742,253× центр. район + 159,85× ж.д. район + 192,105×киров. район +87,1639×красноф. район + 705,387×евро + 107,805 ×сост. хорошее + 312,955× сост. отл. – 243,795 ×индив. планир. + 105,194 ×этаж (ни 1, ни последний) +83,0739 ×кирпичн. – 128,594× санузел. разд. – 331,679 ×сталинка – 138,78× хрущевка – 56,3839 ×тел.
Далее идет идентификация модели: проверка на гетероскедастичность и автокоррелированность остатков.Значение Probability < 0,05, следовательно, нулевую гипотезу о равенстве дисперсий нельзя отклонить. Поэтому гетероскедастичность в построенной регрессии отсутствует.
Проверку на автокоррелированность1 остатков (е – это оцененные по выборке значения отклонений) провели с помощью теста Дарбина – Уотсона (Durbin – Watson). В нашем случае статистика Дарбина – Уотсона = 1,4. Это означает, автокорреляция остатков отсутствует.
Проводили расчет стоимости квартиры по построенной модели и сравнивали ее с реальной стоимостью. Для расчета были взяты пять случайных квартир из различных районов города.
Таблица 1
Сравнение расчетных и реальных показателей
|
|
Район |
||||
|
ЖД |
Кировский |
Краснофлотский |
Центральный |
Индустриальный |
|
|
Расчетная стоимость |
1896,76 |
1969,09 |
2148,00 |
2534,23 |
1733,82 |
|
Реальная стоимость |
1800,00 |
1900,00 |
2182,11 |
2480,00 |
1680,00 |
Из таблицы 1 видно, что различия в расчетных и реальных стоимостях квартир имеются, но не сильно велики.
Следовательно, можно сделать вывод, что полученная модель соответствует реальным данным и позволяет на своей основе прогнозировать стоимость квартир с различными исходными данными. Таким образом, для этого необходимо всего лишь выбрать параметры интересуемой квартиры (площадь, месторасположение, планировка и тд.) и подставить их в уравнение. В результате расчета мы получим стоимость данной квартиры. Однако использовать эту модель можно с определенной осторожностью, так как она не может дать 100 процентный результат, а лишь отражает среднюю стоимость квартир со схожими параметрами.
Пример расчета:
Двухкомнатная квартира новой планировки в кирпичном доме, расположенном в железнодорожном районе города Хабаровска, общей площадью 53 м2, санузел раздельный, имеется телефон, состояние удовлетворительное, этаж не первый и не последний.
Таблица 2
|
Характеристика |
Параметры |
Значение |
|
Свободный член уравнения |
|
– 996,899 |
|
Общая площадь |
53 |
|
|
Местоположение |
Жд район |
159,85 |
|
Планировка |
Новая |
0 |
|
Санузел |
Раздельный |
– 128,594 |
|
Тип здания |
Кирпичное |
83,0739 |
|
Этаж |
Средний |
105,194 |
|
Наличие телефона |
Есть |
– 56,3896 |
|
Состояние |
Удовл. |
0 |
|
Расчетная стоимость (тыс.руб.) |
2639,87 |
|
|
Фактическая стоимость (тыс.руб.) |
2750 |
|
Итак, стоимость квартиры зависит от следующих факторов:
Местоположение – положительно, при расположении в любом из районов, кроме Индустриального (его брали за базу).
Состояние квартиры – положительно, если это хорошее или отличное состояние, а так же евро (за базу брали состояние, требующее косметического ремонта)
Тип здания – положительно, если дом кирпичный (за базу брали панельный).
Этаж – положительно, если квартира находится на среднем этаже.
Планировка – отрицательно, если это хрущевка, сталинка, индивидуальная.
Общая площадь – положительное влияние.
Литература:
Бушин П. Я. Эконометрика. Практикум по решению и анализу задач : учеб. пособ. –Хабаровск : РИЦ ХГАЭП, 2005. – 88 с.
Еженедельное информационно-справочное издание «Вся недвижимость Хабаровска» (№34 (260) 6 сентября 2010 года)
Информационный портал по недвижимости «gdeetotdom.ru»
[Электронный ресурс] – Режим доступа:
Портал по недвижимости «РосРиэлт-Недвижимость» [Электронный ресурс] – Режим доступа:
Информационный портал «RusArticles.com» [Электронный ресурс] – Режим доступа: http://www.rusarticles.com/nedvizhimost-statya/analiz-cen-rynka-nedvizhimosti-xabarovska-i-prognoz-na-2009-god-1272486.html
Газета объявлений «Из рук в руки» [Электронный ресурс] – Режим доступа: http://www.rri.ru
1 Если значения ε не зависят друг от друга, то говорят, что в остатках должна отсутствовать автокорреляция.