В работе изучаются ![]() -расслоенные формации и классы Фиттинга конечных групп. Получено описание строения
-расслоенные формации и классы Фиттинга конечных групп. Получено описание строения ![]() -спутников некоторых
-спутников некоторых ![]() -расслоенных формаций и классов Фиттинга конечных групп.
-расслоенных формаций и классов Фиттинга конечных групп.
Ключевые слова: конечная группа, класс групп, формация, класс Фиттинга, ![]() -расслоенная формация,
-расслоенная формация, ![]() -расслоенный класс Фиттинга.
-расслоенный класс Фиттинга.
В теории классов конечных групп центральное место занимают такие классы групп, как формации, и двойственные им классы — классы Фиттинга (см., например, [1]). Эффективным средством для изучения классов конечных групп являются функциональные методы, с помощью которых были построены такие важные классы, как локальные и композиционные формации и классы Фиттинга, ![]() -локальные и
-локальные и ![]() -композиционные формации и классы Фиттинга. Исследованиями таких классов групп занимались В. Гашюц, К. Дерк, Т. Хоукс, Л. А. Шеметков, В. А. Ведерников, А. Н. Скиба, Н. Н. Воробьев и многие другие (см., например, [1, 2, 5–7]).
-композиционные формации и классы Фиттинга. Исследованиями таких классов групп занимались В. Гашюц, К. Дерк, Т. Хоукс, Л. А. Шеметков, В. А. Ведерников, А. Н. Скиба, Н. Н. Воробьев и многие другие (см., например, [1, 2, 5–7]).
В настоящей работе изучаются ![]() -расслоенные формации и классы Фиттинга конечных групп, введенные в рассмотрение В. А. Ведерниковым и М. М. Сорокиной в 1999 году [3]. Статья посвящена описанию строения
-расслоенные формации и классы Фиттинга конечных групп, введенные в рассмотрение В. А. Ведерниковым и М. М. Сорокиной в 1999 году [3]. Статья посвящена описанию строения ![]() -спутников ряда
-спутников ряда ![]() -расслоенных формаций и классов Фиттинга.
-расслоенных формаций и классов Фиттинга.
Рассматриваются только конечные группы. В работе используются классические методы теории групп и теории классов групп. Используемые определения и обозначения для групп и классов групп стандартны, их можно найти в [1]. Приведем лишь некоторые из них.
Классом групп называется множество групп, содержащее вместе с каждой своей группой и все группы, ей изоморфные; класс групп ![]() называется формацией, если выполняются условия:
называется формацией, если выполняются условия:
1) если ![]() и
и ![]() , то
, то ![]() ,
,
2) если ![]() и
и ![]() , то
, то ![]() ;
;
Класс групп ![]() называется классом Фиттинга, если выполняются условия:
называется классом Фиттинга, если выполняются условия:
1) если
2) если ![]() и
и ![]() ,
, ![]() ,
, ![]() , то
, то ![]() [1].
[1].
Через ![]() обозначается
обозначается ![]() -корадикал группы
-корадикал группы ![]() , т. е. наименьшая нормальная подгруппа группы
, т. е. наименьшая нормальная подгруппа группы ![]() , фактор-группа по которой принадлежит формации
, фактор-группа по которой принадлежит формации ![]() ;
; ![]() –
–![]() -радикал группы
-радикал группы ![]() , т. е. наибольшая нормальная подгруппа группы
, т. е. наибольшая нормальная подгруппа группы ![]() , принадлежащая классу Фиттинга
, принадлежащая классу Фиттинга ![]() . В дальнейшем
. В дальнейшем ![]() обозначает множество всех простых чисел. Пусть
обозначает множество всех простых чисел. Пусть ![]() – непустое множество групп. Через
– непустое множество групп. Через ![]() обозначается класс групп, порожденный
обозначается класс групп, порожденный ![]() ; в частности
; в частности ![]() — класс всех групп, изоморфных группе
— класс всех групп, изоморфных группе ![]()
![]() — класс всех простых групп, изоморфных композиционным факторам группы
— класс всех простых групп, изоморфных композиционным факторам группы ![]() . Пусть
. Пусть ![]() — класс всех конечных групп,
— класс всех конечных групп, ![]() — класс всех простых конечных групп,
— класс всех простых конечных групп, ![]() — непустой подкласс класса
— непустой подкласс класса ![]() . Если
. Если ![]() , то группа
, то группа ![]() называется
называется ![]() -группой. Через
-группой. Через ![]() обозначается класс всех
обозначается класс всех ![]() -групп;
-групп; ![]() ,
, ![]() [3].
[3].
-
Equation Chapter 1 Section 1
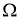 -расслоенные формации конечных групп
-расслоенные формации конечных групп
Функции ![]() {формации групп},
{формации групп}, ![]() {непустые формации Фиттинга}, принимающие одинаковые значения на изоморфных группах из области определения, называются соответственно
{непустые формации Фиттинга}, принимающие одинаковые значения на изоморфных группах из области определения, называются соответственно![]() -функцией и
-функцией и ![]() -функцией [4]. Формация
-функцией [4]. Формация
![]() и
и ![]() для любого
для любого ![]() )
)
называется ![]() -расслоенной формацией с
-расслоенной формацией с ![]() -спутником
-спутником ![]() и направлением
и направлением ![]() и обозначается
и обозначается ![]() [3]. Пусть
[3]. Пусть ![]() . Направление
. Направление ![]()
![]() -расслоенной формации называется
-расслоенной формации называется ![]() -направлением, если
-направлением, если ![]() [4].
[4].
Теорема 1.1. Пусть ![]() ,
, ![]() , где
, где ![]() — произвольная
— произвольная ![]() -функция,
-функция, ![]() —
— ![]() -функция такая, что
-функция такая, что ![]() и для любого
и для любого ![]() выполняется
выполняется ![]() . Тогда
. Тогда ![]() .
.
Доказательство. 1) Установим, что ![]() . Пусть
. Пусть ![]() . Тогда
. Тогда ![]() для любого
для любого ![]() . Поэтому
. Поэтому ![]() . Так как
. Так как ![]() , то
, то ![]() и поэтому
и поэтому ![]() . Это означает, что
. Это означает, что ![]() и
и ![]() . Из
. Из ![]() и
и ![]() получаем, что
получаем, что ![]() и
и ![]() . Таким образом,
. Таким образом, ![]() и, значит,
и, значит, ![]() .
.
2) Покажем, что ![]() . Пусть
. Пусть ![]() . Установим, что
. Установим, что ![]() . Для этого проверим, что выполняются условия:
. Для этого проверим, что выполняются условия: ![]() (а) и
(а) и ![]() для любого
для любого ![]() (б). Так как
(б). Так как ![]() , то
, то ![]() . Следовательно, (а) верно. Пусть
. Следовательно, (а) верно. Пусть ![]() . Так как
. Так как ![]() , то
, то ![]() и поэтому
и поэтому ![]() . Таким образом, (б) верно. Следовательно,
. Таким образом, (б) верно. Следовательно, ![]() и
и ![]() .
.
Из 1) и 2) получаем, что ![]() . Тем самым установлено, что класс
. Тем самым установлено, что класс ![]() всех единичных групп является
всех единичных групп является ![]() -расслоенной формацией с
-расслоенной формацией с ![]() -спутником
-спутником ![]() , описанным в условии теоремы, и любым направлением
, описанным в условии теоремы, и любым направлением ![]() . Теорема доказана.
. Теорема доказана.
Теорема 1.2. Пусть ![]() ,
, ![]() , где
, где ![]() — произвольная
— произвольная ![]() -функция,
-функция, ![]() —
— ![]() -функция такая, что
-функция такая, что ![]() и для любого
и для любого ![]() выполняется
выполняется ![]() . Тогда
. Тогда ![]() .
.
Доказательство. 1) Пусть
2) Пусть ![]() . Покажем, что
. Покажем, что ![]() . Для этого проверим, что выполняются следующие условия:
. Для этого проверим, что выполняются следующие условия: ![]() (а) и
(а) и ![]() для любого
для любого ![]() (б). Так как
(б). Так как ![]() и
и ![]() — формация, то
— формация, то ![]() . Поскольку
. Поскольку ![]() то
то ![]() . Следовательно, (а) верно. Пусть
. Следовательно, (а) верно. Пусть ![]() . Так как
. Так как ![]() и
и ![]() — формация, то
— формация, то ![]() Поскольку
Поскольку ![]() , то
, то ![]() . Таким образом, (б) верно. Следовательно,
. Таким образом, (б) верно. Следовательно, ![]() и, значит,
и, значит, ![]() .
.
Из 1) и 2) получаем, что ![]() . Тем самым установлено, что класс
. Тем самым установлено, что класс ![]() всех конечных групп является
всех конечных групп является ![]() -расслоенной формацией с
-расслоенной формацией с ![]() -спутником
-спутником ![]() , описанным в условии теоремы, и любым направлением
, описанным в условии теоремы, и любым направлением ![]() . Теорема доказана.
. Теорема доказана.
Теорема 1.3. Пусть ![]() ,
, ![]() , где
, где ![]()
![]() произвольная
произвольная ![]() -функция,
-функция, ![]() —
— ![]() -функция такая, что
-функция такая, что ![]() и для любого
и для любого ![]() выполняется
выполняется ![]() . Тогда
. Тогда ![]() .
.
Доказательство. 1) Покажем, что ![]() . Пусть
. Пусть ![]() . Так как
. Так как ![]() — формация, то
— формация, то ![]() . Покажем, что для любого
. Покажем, что для любого ![]() справедливо
справедливо ![]() Действительно, так как
Действительно, так как ![]() , то
, то ![]() . Это означает, что не существует таких
. Это означает, что не существует таких ![]() , для которых
, для которых ![]() . Поэтому утверждение о том, что
. Поэтому утверждение о том, что ![]() для любого
для любого ![]() , верно. Таким образом,
, верно. Таким образом, ![]() и
и ![]() .
.
2) Покажем, что ![]() . Пусть
. Пусть ![]() . Тогда
. Тогда ![]() (а) для любого
(а) для любого ![]() . Далее, для любого
. Далее, для любого![]() по заданию функции
по заданию функции ![]() выполняется
выполняется ![]() (б). Таким образом, утверждения (а) и (б) выполняются одновременно. Это возможно в единственном случае, когда
(б). Таким образом, утверждения (а) и (б) выполняются одновременно. Это возможно в единственном случае, когда ![]() . Следовательно,
. Следовательно, ![]() . Таким образом,
. Таким образом, ![]() .
.
Из 1) и 2) получаем, что ![]() . Тем самым установлено, что класс
. Тем самым установлено, что класс ![]() всех конечных
всех конечных ![]() -групп является
-групп является ![]() -расслоенной формацией с
-расслоенной формацией с ![]() -спутником
-спутником ![]() , описанным в условии теоремы, и любым направлением
, описанным в условии теоремы, и любым направлением ![]() . Теорема доказана.
. Теорема доказана.
Теорема 1.4. Пусть ![]() ,
, ![]() ,
, ![]() , где
, где ![]() —
— ![]() -направление,
-направление, ![]() —
— ![]() -функция такая, что
-функция такая, что ![]() и для любого
и для любого ![]() выполняется
выполняется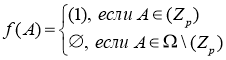 . Тогда
. Тогда ![]() .
.
Доказательство. 1) Покажем, что ![]() . Пусть
. Пусть ![]() . Так как
. Так как ![]() , то по заданию функции
, то по заданию функции ![]() имеем
имеем ![]() . Для любого
. Для любого ![]() из того, что
из того, что ![]() , следует, что
, следует, что ![]() Тогда по условию теоремы
Тогда по условию теоремы ![]() . Следовательно, достаточно показать, что
. Следовательно, достаточно показать, что ![]() . Действительно, так как
. Действительно, так как ![]() и
и ![]() —
— ![]() -направление, то
-направление, то ![]() . Поэтому
. Поэтому ![]() и
и ![]() . Это означает, что
. Это означает, что ![]() . Таким образом,
. Таким образом, ![]() и
и ![]() .
.
2) Покажем, что ![]() . Пусть
. Пусть ![]() . Тогда
. Тогда ![]() . Поскольку
. Поскольку ![]() , то для любого
, то для любого ![]() справедливо
справедливо ![]() . Следовательно, по заданию функции
. Следовательно, по заданию функции ![]() для любого
для любого ![]() выполняется
выполняется ![]() . Поэтому
. Поэтому ![]() , откуда
, откуда ![]() . Тогда
. Тогда ![]() Таким образом,
Таким образом, ![]() и
и ![]() .
.
Из 1) и 2) получаем, что ![]() . Поэтому класс
. Поэтому класс ![]() всех конечных
всех конечных ![]() -групп является
-групп является ![]() -расслоенной формацией с
-расслоенной формацией с ![]() -спутником
-спутником ![]() , описанным в условии теоремы, и любым
, описанным в условии теоремы, и любым ![]() -направлением
-направлением ![]() . Теорема доказана.
. Теорема доказана.
Теорема 1.5. Пусть
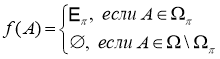 .
.
Тогда ![]() .
.
Доказательство. 1) Покажем, что ![]() . Пусть
. Пусть ![]() . Так как
. Так как ![]() , то
, то ![]() . Для любого
. Для любого ![]() из
из ![]() следует, что
следует, что ![]() Поэтому
Поэтому ![]() и, значит,
и, значит, ![]() . Тогда
. Тогда ![]() . Таким образом,
. Таким образом, ![]() и
и ![]() .
.
2) Покажем, что ![]() . Пусть
. Пусть ![]() . Тогда
. Тогда ![]() и для любого
и для любого ![]() справедливо
справедливо ![]() . Следовательно, по заданию функции
. Следовательно, по заданию функции ![]() для любого
для любого ![]() выполняется
выполняется ![]() . Так как
. Так как ![]() , то
, то ![]() . Поэтому
. Поэтому ![]() и, значит,
и, значит, ![]() .
.
Из 1) и 2) получаем, что ![]() . Таким образом, класс
. Таким образом, класс ![]() всех конечных
всех конечных ![]() -групп является
-групп является ![]() -расслоенной формацией с
-расслоенной формацией с ![]() -спутником
-спутником ![]() , описанным в условии теоремы, и любым направлением
, описанным в условии теоремы, и любым направлением ![]() . Теорема доказана.
. Теорема доказана.
2. ![]() -расслоенные классы Фиттинга конечных групп
-расслоенные классы Фиттинга конечных групп
Функции ![]() {классы Фиттинга групп},
{классы Фиттинга групп}, ![]() {непустые формации Фиттинга}, принимающие одинаковые значения на изоморфных группах из области определения, называются соответственно
{непустые формации Фиттинга}, принимающие одинаковые значения на изоморфных группах из области определения, называются соответственно ![]() -функцией и
-функцией и ![]() -функцией [3]. Класс Фиттинга
-функцией [3]. Класс Фиттинга
![]() и
и ![]() для любого
для любого ![]() )
)
называется ![]() -расслоенным классом Фиттинга с
-расслоенным классом Фиттинга с ![]() -спутником
-спутником ![]() и направлением
и направлением ![]() и обозначается
и обозначается ![]() [3]. Пусть
[3]. Пусть ![]() Направление
Направление ![]()
![]() -расслоенного класса Фиттинга называется
-расслоенного класса Фиттинга называется ![]() -направлением, если
-направлением, если ![]() [4].
[4].
Теорема 2.1. Пусть ![]() ,
, ![]() , где
, где ![]() — произвольная
— произвольная ![]() -функция,
-функция, ![]() —
— ![]() -функция такая, что
-функция такая, что ![]() и для любого
и для любого ![]() выполняется
выполняется ![]() . Тогда
. Тогда ![]()
Доказательство. 1) Установим, что ![]() Пусть
Пусть ![]() Тогда
Тогда ![]() . Поэтому
. Поэтому ![]() . Таким образом,
. Таким образом, ![]() . Это означает, что
. Это означает, что ![]() . Далее, так как
. Далее, так как ![]() , то
, то ![]() и, значит,
и, значит, ![]() . Поэтому второе условие из определения
. Поэтому второе условие из определения ![]() выполняется. Следовательно,
выполняется. Следовательно, ![]() и
и ![]()
2) Покажем, что
Из 1) и 2) следует, что ![]() Тем самым установлено, что класс
Тем самым установлено, что класс ![]() —
— ![]() -расслоенный класс Фиттинга с
-расслоенный класс Фиттинга с ![]() -спутником
-спутником ![]() , описанным в условии теоремы, и любым направлением
, описанным в условии теоремы, и любым направлением ![]() . Теорема доказана.
. Теорема доказана.
Теорема 2.2. Пусть ![]() ,
, ![]() где
где ![]()
![]() произвольная
произвольная ![]() -функция,
-функция, ![]()
![]()
![]() -функция такая, что
-функция такая, что ![]() и для любого
и для любого ![]() выполняется
выполняется ![]() Тогда
Тогда ![]()
Доказательство. 1) Покажем, что ![]() . Пусть
. Пусть ![]() . Тогда
. Тогда ![]() и
и ![]() для любого
для любого ![]() . Следовательно,
. Следовательно, ![]() . Поэтому
. Поэтому ![]() .
.
2) Покажем, что ![]() . Так как
. Так как ![]()
![]() множество всех конечных групп, а
множество всех конечных групп, а ![]() состоит только из конечных групп, то
состоит только из конечных групп, то ![]() .
.
Из 1) и 2) следует, что ![]() . Тем самым установлено, что
. Тем самым установлено, что ![]() —
— ![]() -расслоенный класс Фиттинга с
-расслоенный класс Фиттинга с ![]() -спутником
-спутником ![]() , описанным в условии теоремы, и направлением
, описанным в условии теоремы, и направлением ![]() для любой
для любой ![]() -функции
-функции ![]() . Теорема доказана.
. Теорема доказана.
Теорема 2.3. Пусть ![]() ,
, ![]() , где
, где ![]() — произвольная
— произвольная ![]() -функция,
-функция, ![]() —
— ![]() -функция такая, что
-функция такая, что ![]() и для любого
и для любого ![]() выполняется
выполняется ![]() . Тогда
. Тогда ![]() .
.
Доказательство. 1) Покажем, что ![]() Пусть
Пусть ![]() Так как
Так как ![]() и
и ![]() — класс Фиттинга, то
— класс Фиттинга, то ![]() . Покажем, что для любого
. Покажем, что для любого ![]() справедливо
справедливо ![]() . Действительно, так как
. Действительно, так как ![]() , то
, то ![]() и, значит,
и, значит, ![]() . Поскольку
. Поскольку ![]() , то
, то ![]() . Следовательно, утверждение о том, что
. Следовательно, утверждение о том, что ![]() для любого
для любого ![]() , верно. Таким образом,
, верно. Таким образом, ![]() и
и ![]()
2) Покажем, что ![]() . Пусть
. Пусть ![]() . Проверим, что
. Проверим, что ![]() . Так как
. Так как ![]() , то
, то ![]() (а) для любого
(а) для любого ![]() . С другой стороны, для любого
. С другой стороны, для любого![]() по заданию функции
по заданию функции ![]() выполняется
выполняется ![]() (б). Из (а) и (б) следует, что
(б). Из (а) и (б) следует, что ![]() и, значит,
и, значит, ![]() . Следовательно,
. Следовательно, ![]() Таким образом,
Таким образом, ![]() .
.
Из 1) и 2) получаем, что ![]() Тем самым установлено, что
Тем самым установлено, что ![]() —
— ![]() -расслоенный класс Фиттинга с
-расслоенный класс Фиттинга с ![]() -спутником
-спутником ![]() , описанным в условии теоремы, и любым направлением
, описанным в условии теоремы, и любым направлением ![]() . Теорема доказана.
. Теорема доказана.
Теорема 2.4. Пусть ![]() ,
, ![]() ,
, ![]() , где
, где ![]() —
— ![]() - направление
- направление ![]() -расслоенного класса Фиттинга,
-расслоенного класса Фиттинга, ![]()
![]()
![]() -функция такая, что
-функция такая, что ![]() и для любого
и для любого ![]() выполняется
выполняется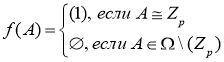 .
.
Тогда
Доказательство. 1) Покажем, что ![]() Пусть
Пусть ![]() . Так как
. Так как ![]() , то
, то ![]() . Пусть
. Пусть![]() . Установим, что
. Установим, что ![]() . Поскольку
. Поскольку ![]() и
и ![]() , то
, то ![]() Отсюда следует, что
Отсюда следует, что ![]() Поэтому достаточно показать, что
Поэтому достаточно показать, что ![]() . Действительно, так как
. Действительно, так как ![]() и
и ![]() , то
, то ![]() . Отсюда следует, что
. Отсюда следует, что ![]() . Таким образом,
. Таким образом, ![]() и
и ![]() .
.
2) Покажем, что ![]() . Пусть
. Пусть ![]() Тогда
Тогда ![]() и для любого
и для любого ![]() справедливо
справедливо ![]() . Согласно заданию
. Согласно заданию ![]() , для любого
, для любого ![]() справедливо
справедливо ![]() . Таким образом,
. Таким образом, ![]() и
и ![]() . Отсюда следует, что
. Отсюда следует, что ![]() и, значит,
и, значит, ![]() .
.
Из 1) и 2) следует, что ![]() . Тем самым установлено, что
. Тем самым установлено, что ![]() —
— ![]() -расслоенный класс Фиттинга с
-расслоенный класс Фиттинга с ![]() -спутником
-спутником ![]() , описанным в условии теоремы, и любым
, описанным в условии теоремы, и любым ![]() -направлением
-направлением ![]() . Теорема доказана.
. Теорема доказана.
Теорема 2.5. Пусть ![]() ,
, ![]() ,
, ![]() ,
, ![]() , где
, где ![]() — произвольная
— произвольная ![]() -функция,
-функция, ![]() —
— ![]() -функция такая, что
-функция такая, что ![]() и для любого
и для любого ![]() справедливо
справедливо 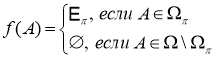 . Тогда
. Тогда ![]()
Доказательство. 1) Покажем, что ![]() Пусть
Пусть ![]() Тогда
Тогда ![]() , то
, то ![]() . Пусть
. Пусть![]() . Покажем, что
. Покажем, что ![]() . Так как
. Так как ![]() , то
, то ![]() . Пусть
. Пусть ![]() . Покажем, что
. Покажем, что ![]() . Так как
. Так как ![]() и
и ![]() то
то ![]() . Отсюда следует, что
. Отсюда следует, что ![]() по условию теоремы. Поскольку
по условию теоремы. Поскольку ![]() , то
, то ![]() . Таким образом,
. Таким образом, ![]() , и поэтому
, и поэтому ![]()
2) Покажем, что ![]() . Пусть
. Пусть ![]() . Тогда
. Тогда ![]() и для любого
и для любого ![]() справедливо
справедливо ![]() . По заданию
. По заданию ![]() для любого
для любого ![]() выполняется
выполняется ![]() . Отсюда следует, что
. Отсюда следует, что ![]() . Из
. Из ![]() следует, что
следует, что ![]() . Поэтому
. Поэтому ![]() . Так как
. Так как ![]() , то
, то ![]() .
.
Из 1) и 2) следует, что ![]() Тем самым установлено, что
Тем самым установлено, что ![]() —
— ![]() -расслоенный класс Фиттинга с
-расслоенный класс Фиттинга с ![]() -спутником
-спутником ![]() , описанным в условии теоремы, и любым направлением
, описанным в условии теоремы, и любым направлением ![]() . Теорема доказана.
. Теорема доказана.
Литература:
- Doerk, K. Finite soluble groups / K. Doerk, T. Нawkes. — Berlin — New York: Walter de Gruyter, 1992. — 901 с.
- Gaschutz, W. Zur Theorie der endlichen auflosbaren Gruppen / W. Gaschutz // Math. Z. — 1963. V. 80, N 4. — P. 300−305.
-
Ведерников, В. А., Сорокина, М. М.
 -расслоенные формации и классы Фиттинга конечных групп / В. А. Ведерников, М. М. Сорокина // Дискретная математика. — 2001. — Том 13, Выпуск 3. — С. 125–144.
-расслоенные формации и классы Фиттинга конечных групп / В. А. Ведерников, М. М. Сорокина // Дискретная математика. — 2001. — Том 13, Выпуск 3. — С. 125–144.
-
Ведерников, В. А. Максимальные спутники
 -расслоенных формаций и классов Фиттинга / В. А. Ведерников // Труды ИММ УрО РАН. — 2001. — Том 7, № 2. — С. 55–71.
-расслоенных формаций и классов Фиттинга / В. А. Ведерников // Труды ИММ УрО РАН. — 2001. — Том 7, № 2. — С. 55–71.
- Воробьев Н. Н. Алгебра классов конечных групп. — Витебск: ВГУ имени П. М. Машерова, 2012. — 322 с.
- Скиба, А. Н. Алгебра формаций / А. Н. Скиба. — Минск: Беларуская навука, 1997. — 240 с.
- Шеметков, Л. А. Формации конечных групп / Л. А. Шеметков. — М.: Наука, 1978. — 272 с.







