Целью данной работы является расчет плотностного и пустотного эффектов реактивности на примере реактора типа БРЕСТ со свинцовым охлаждением. Исследуется положительный эффект реактивности (ПЭР) — полное или частичное осушении активной зоны ядерного реактора при попадании в неё газовых пузырей или разгерметизации трубок первого контура. Основная задача состоит в минимизации спектральной составляющей ПЭР. При небольших размерах активной зоны утечка нейтронов столь велика, что несмотря на положительную составляющую спектрального коэффициента суммарный пустотный эффект будет заведомо отрицательным. Основная расчетная модель строится на решении интегро-дифференциального уравнения переноса нейтронов методом дискретных ординат, реализованного в программном комплексе «WIMS32D4». Полученные результаты можно использовать при разработке быстрых реакторов естественной безопасности со свинцовым охлаждением.
Ключевые слова: уравнение переноса нейтронов, плотностной эффект реактивности, коэффициент размножения нейтронов, реактивность, wims.
Значительного повышения безопасности ядерных реакторов деления можно добиться в рамках существующих технологий. Наибольшим потенциалом безопасности из существующих установок обладают реакторы на быстрых нейтронах с жидкометаллическим теплоносителем. В современных реакторах в качестве теплоносителя используется натрий, обладающий высокой химической активностью. В результате необходима трёхконтурная схема преобразования энергии, позволяющая исключить прямой контакт радиоактивного натрия первого контура с водой (паром) третьего ввиду взрывного характера. Отказ от натриевого теплоносителя в пользу химически относительно инертного свинца позволит в принципе исключить промежуточный контур, тем самым упростив и удешевив конструкцию ядерной энергетической установки. В БРЕСТ применяется двухконтурная схема преобразования энергии: первый контур — свинцовый теплоноситель, второй контур — водяной пар.
Введем геометрический объем r = (x, y, z), где x, y, z — координаты нейтрона; Ω = (φ, θ) — единичный вектор, характеризующий направление полета нейтрона, где φ, θ — полярный (азимутальный) и аксиальный (зенитный) углы соответственно; кинетическую энергию E; время t.
Введем пространственно-временную дифференциальную энергетически угловую плотность потока нейтронов Ф (r, Ω, E, t) = [см-2 · с-1 · ср-1 · эВ-1]. Введем плотность нейтронов N (r, Ω, E, t) = [см-3 · ср-1 · эВ-1],
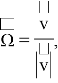
где v — средняя скорость нейтрона.
![]()
Составим уравнение баланса нейтронов [1]. Предположим, что изменение плотности dN за единицу времени dt обусловлено разностью скоростей прибыли и убыли нейтронов в элементарном объеме dV = dx · dy · dz:
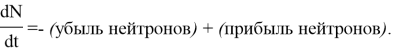
Распишем полную производную в левой части:
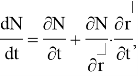
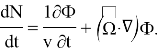
Убыль:
- Поглощение нейтронов (скорость реакции поглощения) в элементарном объеме Σa Ф, где Σa = [см-1] — макроскопическое сечение поглощения;
- Нейтрон может изменить направление полета Ω → Ω'' или скорость E → E'' в результате упругого рассеяния на атомах среды Σs Ф, где Σs — макросечение рассеяния.
Прибыль:
- За счет деления тяжелых ядер (скорость реакции деления) νfΣf Ф в единичном объеме, где Σf — макросечение деления; νf — число нейтронов, рожденных при одном акте деления;
- За счет дополнительных радионуклидных источников Q для безопасного пуска реактора;
- За счет попадания нейтрона из вне в рассматриваемый элементарный объем Ω → Ω', E → E':
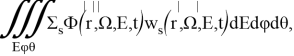
где ws — плотность вероятности того, что нейтрон в процессе рассеяния поменяет вектор скорости v → v'.
Рассмотрим стационарный случай:
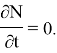
Тогда уравнение баланса нейтронов примет вид:
![]() (1)
(1)
Рассмотрим эквивалентную расчетную ячейку Вигнера-Зейтса, характеризующую поперечное сечение цилиндрической трубки твэла омываемого теплоносителем (рис. 1).
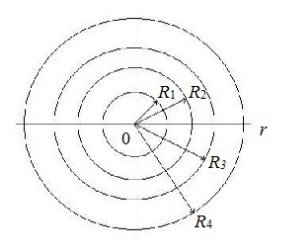
Рис. 1. Расчетная ячейка твэла: R1 — радиус топливной таблетки, R2 — зазор, R3 — оболочка твэла, R4 — теплоноситель
Задаем граничные условия:
- Условие симметрии плотности потока нейтронов на границе r = R4 и в центре r = 0 (плотность потока нейтронов спадает от центра к периферии одинаковым образом во всех направлениях):
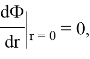
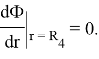
- Условие непрерывности плотности потока нейтронов на границе раздела двух сред (отсутствие разрыва в распределении плотности потока):
![]()
![]()
![]()
Уравнение (1) не имеет аналитического решения. Решение этого уравнения реализуется множеством программ различными методами. Например, программа «WIMS32D4» [3], реализует решение уравнения переноса в 69-групповом приближении (весь диапазон кинетической энергии МэВ возможного излучения нейтронов разделён на 69 поддиапазонов) SN-методом (N=4). Программа разработана в Великобритании, константное обеспечение — файлы оцененных ядерных данных (МАГАТЭ).
Рассмотрим бесконечную решетку твэлов (рис. 2).
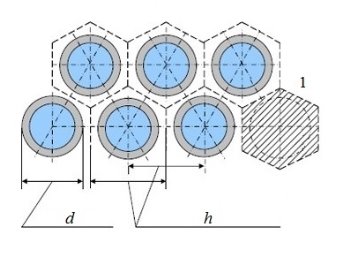
Рис. 2. Треугольная решетка твэлов: 1 — элементарная ячейка, d — диаметр твэла, h — шаг решетки твэлов
Введем коэффициент размножения нейтронов для бесконечной среды как отношение числа нейтронов в настоящем поколении nm к числу нейтронов в предыдущем поколении nm-1, если при этом устремить число рассматриваемых поколений в бесконечность:
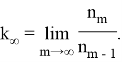
Введем эффективный коэффициент размножения нейтронов:
![]()
где P — вероятность для нейтронов избежать утечки. kэф = 1 соответствует критическому состоянию. Поэтому для достижения критического состояния k∞ должен быть больше 1.
Введем понятие реактивности, которое показывает относительное отклонение коэффициента размножения нейтронов от единицы:
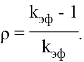
Этот параметр используется для оценки безопасности ядерного реактора. В критическом состоянии значение реактивности равно нулю. Любые изменения расположения топливных стержней, температуры топлива, плотности теплоносителя и т. д. приводят к изменению реактивности.
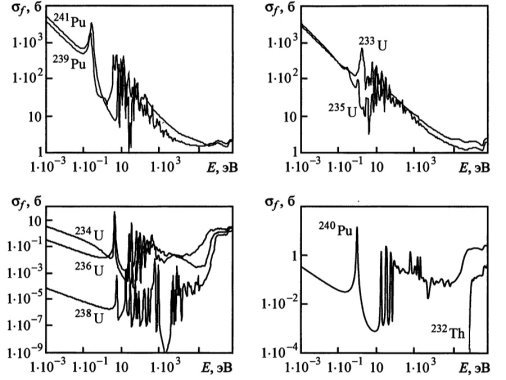
Рис. 3. Микросечения деления для урана-235, урана-238, плутония-239 и других актиноидов
В реакторах на быстрых нейтронах пустотный эффект реактивности реализуется при полном осушении активной зоны, когда плотность теплоносителя близка к нулю. Плотностной эффект реактивности связан с попаданием в активную зону газовых пузырей вследствие разгерметизации трубок твэлов и теплоносителя в первом контуре. Эффект сопровождается уменьшением значения плотности теплоносителя и образованием воздушных прослоек вокруг оболочек твэлов. Это в свою очередь приводит к резкому скачку энергетического спектра образующихся нейтронов деления в область более высоких энергий, и как следствие увеличивается вероятность реакции деления для различных долгоживущих актиноидов в обогащенной среде (рис. 3). В этом случае наблюдается положительный пустотный эффект реактивности. Его можно скомпенсировать утечкой нейтронов, которая дает отрицательный вклад, для чего создается плоская активная зона. Утечка регулируется параметром уплощения.
Предлагается рассчитать параметр реактивности при возникновении положительного пустотного эффекта в активной зоне реактора БРЕСТ (свинцовый теплоноситель). Полученный результат представлен на рис. 4.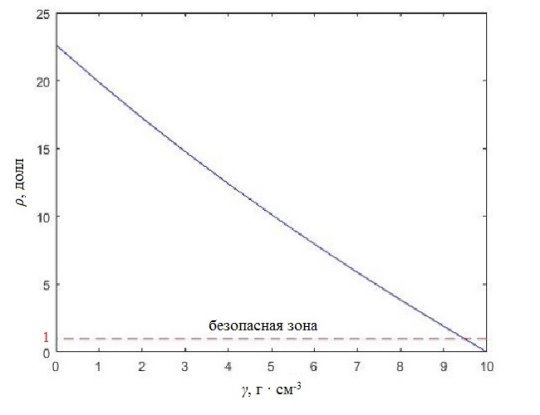
Рис. 4. Зависимость параметра реактивности ρ, посчитанного в долях запаздывающих нейтронов, от падения плотности теплоносителя γ
Как и ожидалось для бесконечной решетки твэлов (при отсутствии утечки нейтронов) плотностной эффект вносит положительный вклад в реактивность. Из графика можно заметить, что зависимость близка к линейной. При значениях ρ меньше 1 реактор можно считать безопасным.
Основная задача расчетных исследований состоит в минимизации спектральной составляющей положительного пустотного эффекта реактивности.
Для примера рассмотрим случай, когда увеличивается доля теплоносителя в решетке твэлов при постоянной доле топлива и наоборот.
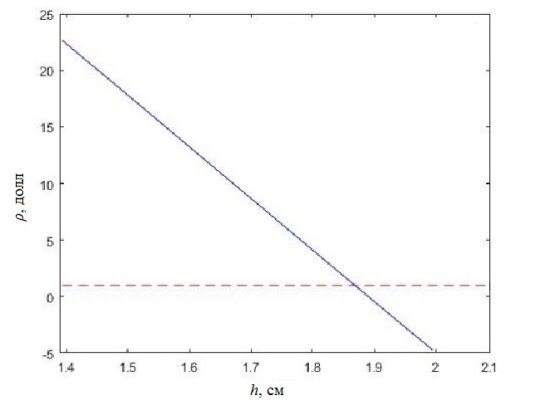
Рис. 5. Зависимость параметра реактивности ρ от шага решетки твэлов h
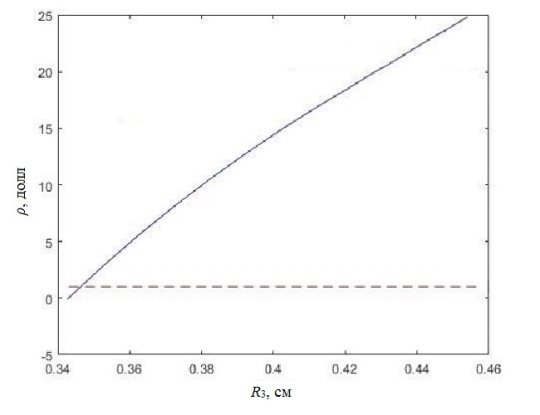
Рис. 6. Зависимость параметра реактивности ρ от радиуса твэла R3
Согласно полученным результатам (рис. 5, 6), установлено, что для реакторов большой мощности с малой утечкой нейтронов из активной зоны для минимизации спектральной составляющей положительного пустотного эффекта реактивности целесообразно либо увеличивать шаг решетки твэлов более чем на 0,6 см, либо уменьшать диаметр трубки твэла на 0,2 см.
Исходя из полученных результатов для оценки безопасности реакторов нового поколения можно сделать вывод, что спектральная составляющая пустотного эффекта реактивности снижается при увеличении шага решетки твэла, а также при уменьшении диаметра твэла. Данный результат характерен для бесконечной решетки твэлов реактора БРЕСТ любой мощности.
Используя предложенные тепловыделяющие сборки можно создать реактор, у которого плотностной эффект реактивности будет отрицательным, что говорит о безопасности реактора при появлении газовых пузырей в процессе работы.
Литература:
- Окунев В. С. Основы прикладной ядерной физики и введение в физику ядерных реакторов / Учеб. пособие. Сер.: Физика в техническом университете. 2-е изд., испр. и доп. — М.: Издательство МГТУ им. Н. Э. Баумана, 2015. — 536 с.
- Кадилин В. В., Рябева Е. В., Самосадный В. Т. Прикладная нейтронная физика: учебное пособие. — М.: НИЯУ МИФИ, 2011. — 124 с.
- Окунев В. С. Нейтронно-физический расчёт решётки ядерного реактора на основе газокинетической теории переноса: учеб. пособие / В. С. Окунев, И. С. Лисицын; под ред. В. И. Солонина. — М.: Изд-во МГТУ им. Н. Э. Баумана, 2011. — 145 c.: ил.







