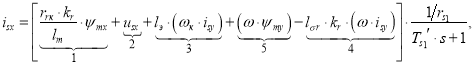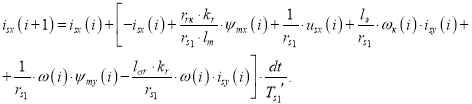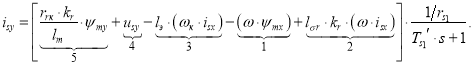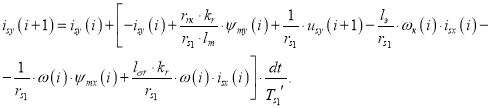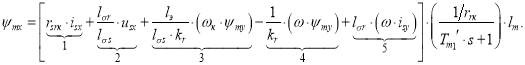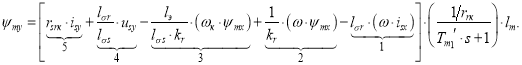В данной работе дадим сравнение математических моделей асинхронного двигателя с переменными is – ψm в Matlab-Simulink, Matlab-Script и Си.
1. Определение статорного тока isx
Matlab-Simulink:
В работе [1] была получена структурная схема для определения статорного тока isx в Simulink (рис. 1) по следующему уравнению:
|
|
(1) |
где![]() - постоянная времени статорной обмотки.
- постоянная времени статорной обмотки.
Matlab-Script:
Преобразуем уравнение (1) для программирования в Matlab-Script:
![]()
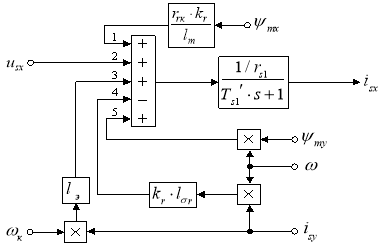
Рис. 1. Структурная схема для определения тока isx в Simulink
Переходим к оригиналу (s = d/dt):
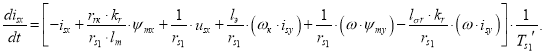
Переходим к конечным разностям (метод Эйлера):
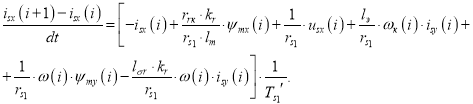
Отсюда ток isx в Matlab-Script определится следующим образом [1]:
|
|
(1') |
Си:
Исключив (i) и (i+1) из (1’), получим выражение isx на языке Си:
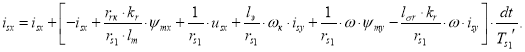
Видимо, если циклы будут составлять несколько сотен тысяч, то это скажется на быстродействии.
2. Определение статорного тока isy
Уравнение для определения тока isy в Simulink, полученное в работе [1]:
|
|
(2) |
Структурная схема реализации уравнения (2) приведена на рис. 2.
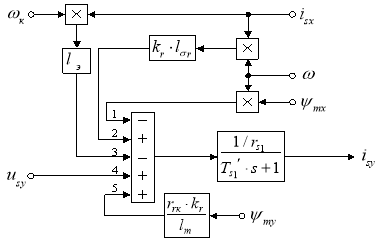
Рис. 2. Структурная схема для определения тока isy в Simulink
Аналогично преобразуем выражение тока isy для Matlab-Script [1]:
|
|
(2') |
Из уравнения (2’) получим выражение isy для программирования на Си:
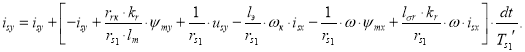
3. Определение потокосцепления ψmx
В работе [1] была получена структурная схема для определения потокосцепления ψmx в Simulink (рис. 3) по следующему уравнению:
|
|
(3) |
где![]() - постоянная времени потокосцепления в воздушном зазоре.
- постоянная времени потокосцепления в воздушном зазоре.
Преобразуем уравнение (3) для программирования в Matlab-Script:
![]()

Рис. 3. Структурная схема для определения потокосцепления ψmx в Simulink
Переходим к оригиналу:
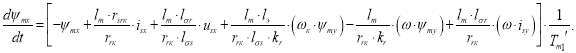
Переходим к конечным разностям:
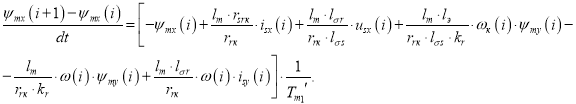
Определим потокосцепление ψmx в Matlab-Script:
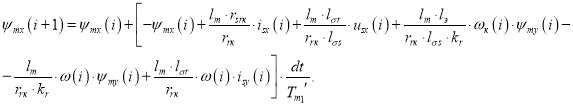
Уравнение потокосцепления ψmx для программирования на языке Си:
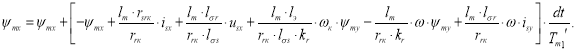
4. Определение потокосцепления ψmy
Уравнение ψmy в Simulink, полученное в работе [1], имеет вид:
|
|
(4) |
Структурная схема реализации уравнения (4) приведена на рис. 4.
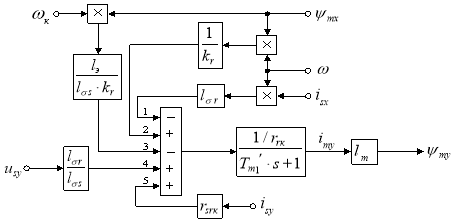
Рис. 4. Структурная схема для определения потокосцепления ψmy в Simulink
Аналогично преобразуем выражение ψmy для Matlab-Script [1]:
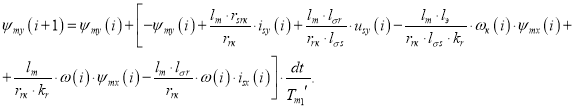
Уравнение ψmy для программирования на языке Си будет иметь вид:
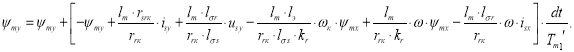
На рис. 5 представлена структурная схема для реализации уравнения электромагнитного момента в Matlab-Simulink:
![]()
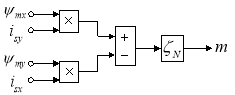
Рис. 5. Математическая модель электромагнитного момента m в Simulink
Уравнение электромагнитного момента для Matlab-Script:
![]()
Уравнение электромагнитного момента для реализации на языке Си:
![]()
Электрическая скорость вращения ротора в Simulink (рис. 6):
![]()
где![]() - механическая угловая скорость на валу двигателя.
- механическая угловая скорость на валу двигателя.
![]()
Рис. 6. Математическая модель определения электрической скорости вращения ротора в Simulink
Определение электрической скорости вращения ротора в Matlab-Script:
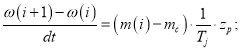
![]()
Уравнение электрической скорости на языке Си:
![]()
Математическая модель асинхронного двигателя с короткозамкнутым ротором с переменными is – ψm на выходе апериодических звеньев приведена на рис. 8. Параметры асинхронного двигателя рассмотрены в работах [2] и [3].
Расчет параметров производим в Script (рис. 7).
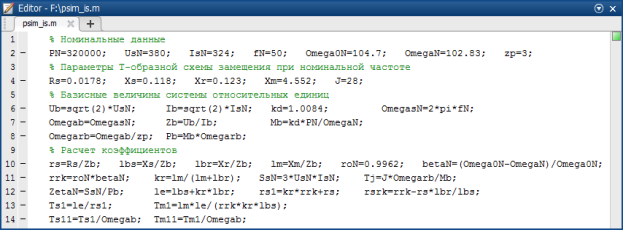
Рис. 7. Расчет параметров асинхронного двигателя в Script
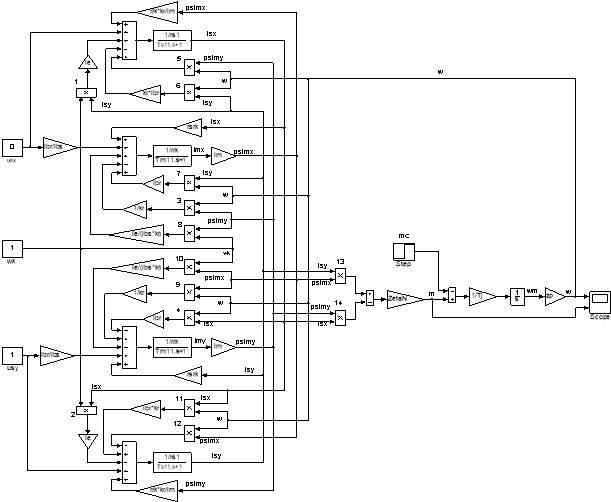
Рис. 8. Математическая модель асинхронного двигателя с переменными is – ψm на выходе апериодических звеньев в Matlab-Simulink
Результаты моделирования асинхронного двигателя в Simulink представлены на рис. 9.
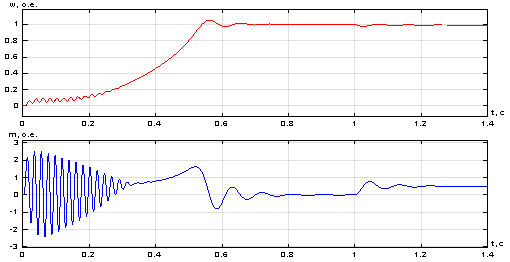
Рис. 9. Графики скорости и электромагнитного момента в Simulink
Реализация математической модели асинхронного двигателя с короткозамкнутым ротором с переменными is – ψm в Matlab-Script в системе относительных единиц приведена на рис. 10.
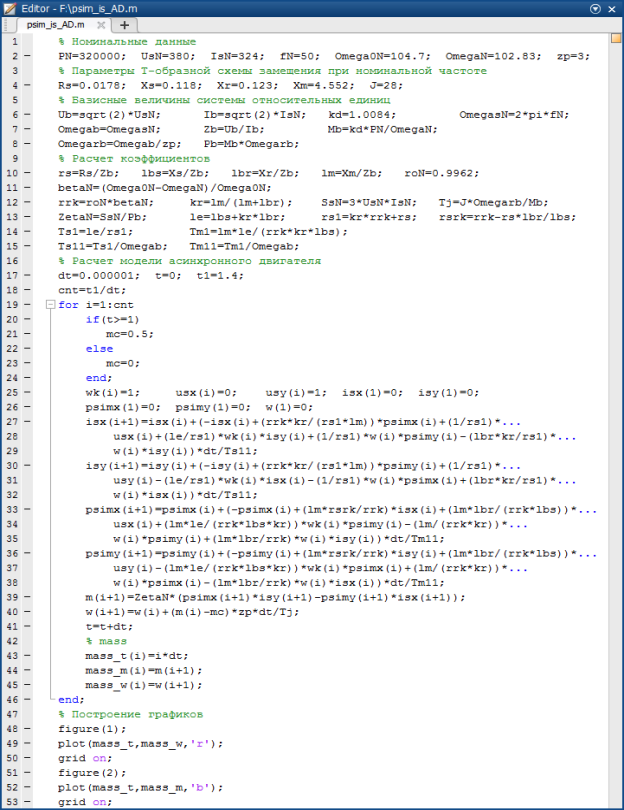
Рис. 10. Математическая модель асинхронного двигателя с переменными is – ψm в Matlab-Script
Результаты моделирования асинхронного двигателя в Matlab-Script даны на рис. 11.
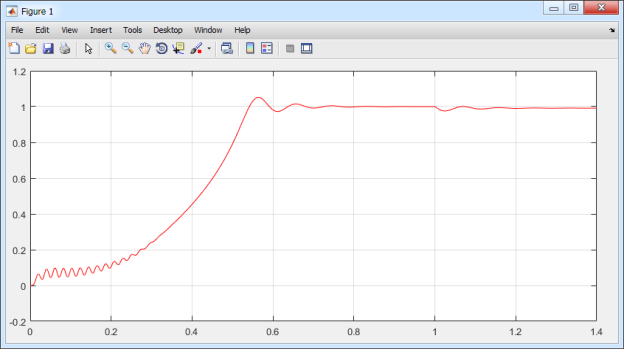
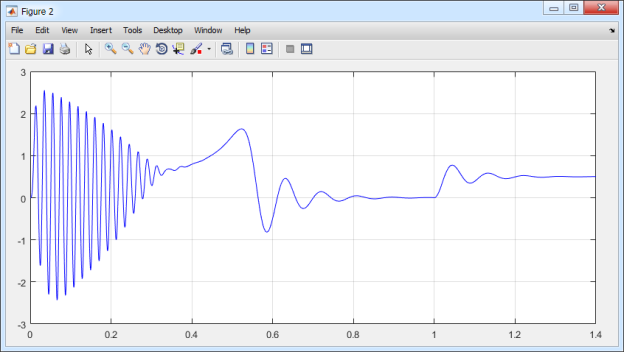
Рис. 11. Графики скорости и электромагнитного момента в Matlab-Script
Математическая модель асинхронного двигателя с переменными is – ψm на языке программирования Си дана на рис. 12.
Результаты моделирования асинхронного двигателя на языке Си даны на рис. 13.
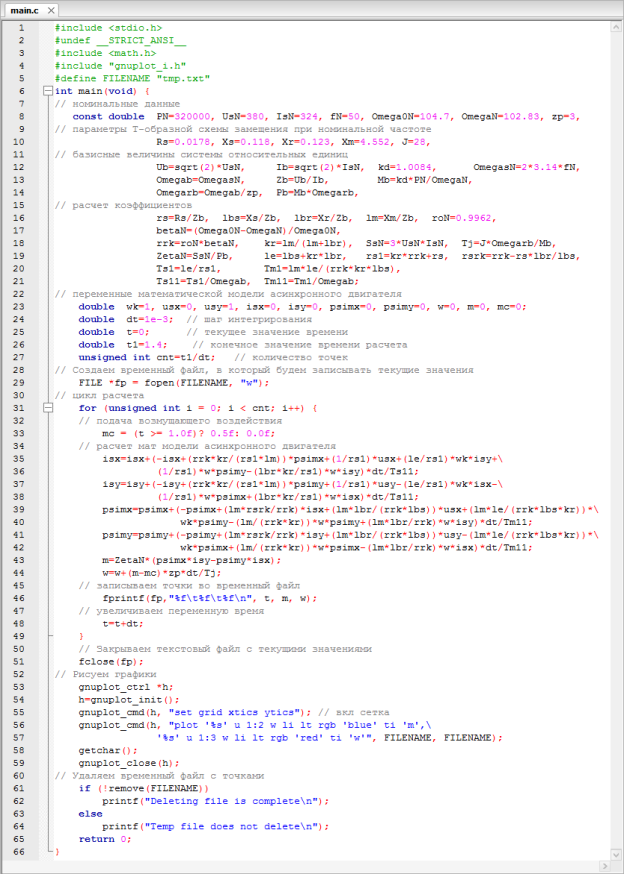
Рис. 12. Математическая модель асинхронного двигателя с переменными is – ψm на языке программирования Си
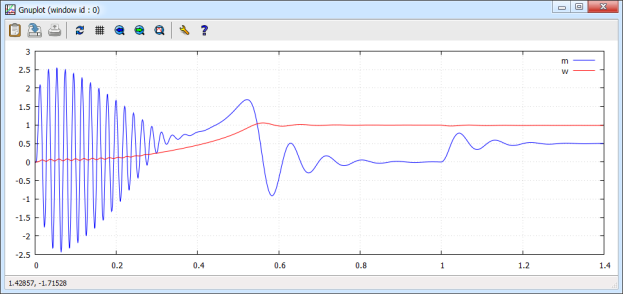
Рис. 13. Графики скорости и электромагнитного момента при моделировании на языке Си
Литература:
- Емельянов А.А., Бесклеткин В.В., Гусев В.М., Камеристов К.В., Артемьев А.В., Насыбуллин Р.Н., Велькер А.В., Шерстобитов А.В., Федотов В.В., Пестеров Д.И. Моделирование асинхронного двигателя с переменными ψm – is в Matlab-Script в системе относительных единиц // Молодой ученый. - 2018. - №48. - С. 1-9.
- Шрейнер Р.Т. Математическое моделирование электроприводов переменного тока с полупроводниковыми преобразователями частоты. - Екатеринбург: УРО РАН, 2000. - 654 с.
- Шрейнер Р.Т. Электромеханические и тепловые режимы асинхронных двигателей в системах частотного управления: учеб. пособие / Р.Т. Шрейнер, А.В. Костылев, В.К. Кривовяз, С.И. Шилин. Под ред. проф. д.т.н. Р.Т. Шрейнера. - Екатеринбург: ГОУ ВПО «Рос. гос. проф.-пед. ун-т», 2008. - 361 с.
- Васильев А.Н. Matlab. Самоучитель. Практический подход. – СПб.: Наука и Техника, 2012. – 448 с.
- Васильев А.Н. Программирование на C++ в примерах и задачах. – М.: Издательство «Э», 2017. – 368 с.