При проектировании автомобильных дорог применяют научно-обоснованные параметры земляного полотна и проезжей части, расположения оси дороги в плане, а также элементов продольного и поперечного профиля. Большое внимание уделяется вопросам обеспечения устойчивости земляного полотна, от решения которых зависит в целом качество проекта дороги. Мероприятия по обеспечению устойчивости земляного полотна имеют особое значение при постройке дорог в горной и пересеченной местности. Они предусматривают применение различных искусственных сооружений. Наиболее распространенными из них являются подпорные стены (ПС), диапазон применения которых очень широк.
К настоящему моменту накопилось большое число типов ПС как по конструкции (массивные, тонкостенные, облегченные, анкерные и т. д.), так и по материалу, из которого они возводятся (каменные, бетонные, бутобетонные, железобетонные и др.). Однако, применительно к современным автодорогам в нашей республике наиболее употребимы сборные железобетонные ПС, обладающие высоким уровнем индустриальности.
Процесс проектирования ПС является достаточно сложным не только по постановке задачи, но и многообразию вариантов решений. Он занимает относительно большой объем, особенно в местностях с большими уклонами, что требует значительных трудозатрат и материалов. Поэтому проблема снижения стоимости и трудоемкости этих конструкций путем оптимального проектирования весьма актуальна.
Данный процесс можно рассматривать как процесс решения многопараметрической задачи, где проектными являются параметры, отражающие с разной степенью подробности факторы, влияющие на расположение ПС. Большинство из них имеют геометрическую природу, вследствие чего процесс проектирования ПС фактически является процессом оптимального геометрического проектирования.
Ключевыми задачами этого процесса являются:
– определение зоны оптимального размещения (ЗОР) (рис.1, а) в теле насыпи автодороги, в пределах которой должна располагаться ПС;
– назначение оптимальных параметров в ПС и ее элементов (блоков, секций) с учетом нормативных технологических и метрических ограничений (в т. ч. стремление к минимизации числа типоэлементов);
– оптимальное расположение ПС в ЗОР.
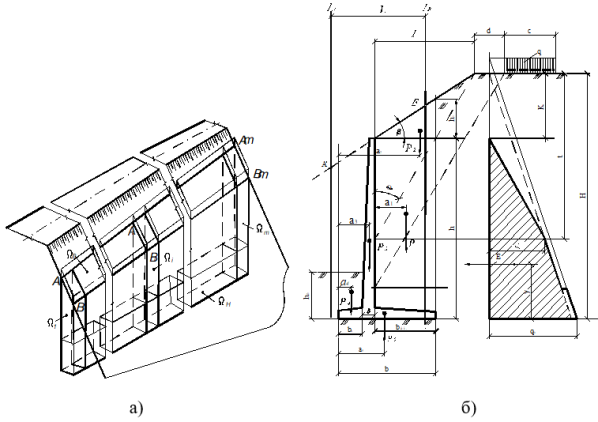
Рис. 1
ЗОР является геометрическим отображением уже упоминавшихся факторов и представляет собой трехмерное тело, которое может иметь довольно сложную структуру в зависимости от действующих ограничений. В общем виде ЗОР может рассматриваться как совокупность ряда составляющих областей в пределах, которых должно обеспечиваться требуемое расположение соответствующих элементов подпорных стен (см. рис.1, а)
![]()
где В — верхняя, Н — нижняя, 1- начальная и m — конечная области. Значение каждой из этих областей в ЗОР, с точки зрения размещения в ней ПС, неодинаково. Так, верхняя В и нижняя Н области предназначены для размещения в них определяющих элементов ПС — верха и низа (подошвы). Следовательно, они в наибольшей степени влияют на характер изменения параметров формы и положения ПС.
Абстрагируясь от подробного рассмотрения процесса формирования границ областей ЗОР, которые является предметом отдельного исследования [1], следует отметить, что верхняя В и нижняя Н области определяются на основании расчетов устойчивости, расчетная схема которой показана на рис. 1, б. Искомыми величинами расчета являются граничные значения длин ![]() и
и ![]() расстояния
расстояния ![]() внутренней грани ПС от бровки земляного полотна дороги, соответствующие предельно-допустимым значениям коэффициента условий работы — [m], принимаемого в зависимости от типа конструкции ПС ее основания.
внутренней грани ПС от бровки земляного полотна дороги, соответствующие предельно-допустимым значениям коэффициента условий работы — [m], принимаемого в зависимости от типа конструкции ПС ее основания.
По расчетным значениям коэффициента условий работы m находят
условия устойчивости ПС против опрокидывания [2], выражаемые
формулой
![]() ,
,
где Мопр — расчетный опрокидывающий момент относительно плоскости подошвы фундамента: Мпред — предельный опрокидывающий момент относительно точки 0; Е— активное (горизонтальное) давление грунта;
у — плечо силы Е относительно плоскости подошвы фундамента; Рi— силы, соответствующие весу грунта и элементов ПС; аi — плечи сил Рi относительно вертикальной прямой, проходящей через точку 0; [m] — предельно-допустимые значения коэффициента m, принимаемые, например, для сечения железобетонных конструкций с фундаментом на нескальном основании — [0.7 0,75].
В настоящей статье рассматривается задача размещения в заданной ЗОР трехмерной ПС с учетом требования назначения ее оптимальных параметров.
Для пояснения сути предлагаемого метода представляется целесообразным рассмотреть его на примере размещения простого геометрического тела (рис.2, а), которого можно принять за абстрактное отображение блока ПС либо его составной части (рис.2, б).
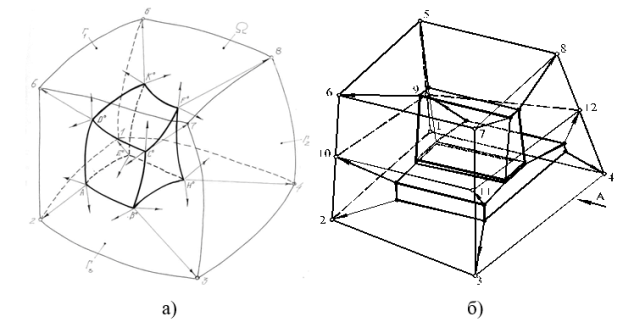
Рис. 2
Как известно, число параметров положения объекта в трехмерном пространстве равно 6. Поэтому задача оптимального размещения трехмерного тела в трехмерном же пространстве в общем виде предполагает определение шести параметров положения с учетом воздействия системы ограничений равенства вида:
С (Х, Y, Z) = O,(1)
причем в качестве геометрических образов (1) могут выступать не только поверхности, но также линии и точки. Учитываются и ограничения-неравенства вида
![]() (2)
(2)
предполагающие инцидентность ограниченным зонам трехмерного пространства. Если сюда добавить условие необходимости управления параметрами формы размещаемого объекта, то целевая функция будет иметь вид
![]() ,
,
где р — массив параметров формы размещаемого объекта. Аналитическое решение такой задачи получить не всегда возможно, поэтому приходится использовать численные и аналоговые методы решения. К последним может быть отнесен статико-геометрический метод проф. С. Н. Ковалева, который был успешно применен для решения двумерных задач размещения [3].
В рассматриваемой постановке размещение объекта выполняется под воздействием условных усилий, приложенных в различных точках объекта и ЗОР. Эти усилия пропорциональны длинам отрезков прямых, соединяющих данные точки, и являются геометрической интерпретацией ограничений вида (1) и (2). С помощью аналогичных усилий осуществляется управление формой размещаемого объекта.
Объект считается оптимально расположенным в ЗОР и имеющим оптимальные размеры, если он находится в состоянии равновесия под действием указанных усилий и удовлетворяет действующим ограничениям. Аналитическим описанием такого условия являются уравнения
![]() ; (3)
; (3)
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
где R x, R y, R z — проекции усилий на оси координат, M x, M y, M z — моменты этих усилий относительно осей соответственно.
Учитывая характер рассматриваемой прикладной задачи, предлагаемый способ целесообразно рассмотреть на примере плоско — параллельного перемещения, что соответствует (3) ![]() (5).
(5).
При размещении трехмерных объектов рассматриваются две группы условных усилий: а) размещающие; б) управления формой.
Под действием первых размещаемый объект, моделируемый своими угловыми точками (узлами), в которых приложены эти усилия, изменяет не только положение, но также форму и размеры. Поэтому вводятся усилия второй группы, назначение которых — восстановить исходные геометрические параметры объекта. Эти же усилия выполняют функцию изменения параметров формы объекта для обеспечения оптимальности размеров объекта по отношению к ЗОР.
Алгоритм размещения организован по итерационному принципу. Исходными данными для расчета служат:
– координаты вершин ЗОР;
– исходные параметры размещаемого объекта;
– массив данных, обеспечивающий соответствие изменяемых параметров объекта действующим нормам;
– система предельных допустимых линейных отклонений.
Исходные параметры размещаемого объекта (его первое приближение) желательно назначать как можно ближе к искомому оптимальному положению. На практике такое условие предполагает отсутствие очевидного грубого различия между размещающими усилиями.
Для каждого узла размещаемого объекта составляются уравнения равновесия вида:
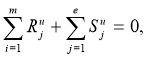
где u-обобщенное обозначение координат, R-размещающие усилия, S-усилия управления формой, m-число размещающих усилий, ![]() -число усилий управления формой. Эти управления в проекциях на координатные оси образуют системы линейных алгебраических уравнения, число которых равно числу угловых точек объекта. В результате решения этих систем определяются координаты узлов очередного приближения.
-число усилий управления формой. Эти управления в проекциях на координатные оси образуют системы линейных алгебраических уравнения, число которых равно числу угловых точек объекта. В результате решения этих систем определяются координаты узлов очередного приближения.
На этапе анализа результата осуществляется сравнение полученных параметров формы и положения, а также проверка соблюдения заданных ограничений с требуемыми значениями и допустимыми отклонениями. В случае, если проверка дает негативный (хотя бы для их элементов) результат, вводятся корректирующие усилия, прикладываемые в узлах и направленные в сторону требуемого положения элемента и пропорциональные длинам связей. В случае необходимости к этим усилиям могут быть введены рациональные коэффициенты, предназначенные для ускорения сходимости процесса. Найденные координаты объекта принимаются в качестве исходных для очередной итерации, и процесс повторяется до тех пор, пока не будет достигнута требуемая точность решения. Следует заметить, что, как и другие методы решения оптимизационных задач, предлагаемый метод также зависит от совместности исходных данных, что предполагает наличие возможности их корректировки.
Литература:
- Синдаров Р. У. Формирования зоны оптимального расположения подпорных стен автомобильных дорог // Прикл. геом. и инж. графика. — 1995.- Вып. 57.- С. 54–56.
- Тетиор А. Н. Облегченные подпорные стены в транспортном строительстве. — М.: Транспорт, 1987. — 79 с.
- Сафронеев И. В., Бабичев А. Н. Универсальный алгоритм размещения элементов сборных оболочек в ячейках паркетирующей сети/ Прикл.геометрия и инж. графика. — 1986. — Вып. 41. — С. 29–31.







