In this article presents logarithmic methods for solving first order and second order differential equations.
Let ![]() ,
, ![]() be Riemann integrable functions;
be Riemann integrable functions; ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
; ![]() ,
, ![]() ,
, ![]() , … ,
, … , ![]() ,
, ![]() ,
, ![]() - is an integration constant. The symbol
- is an integration constant. The symbol ![]() between two formulas will mean that the second formula follows from the first one.
between two formulas will mean that the second formula follows from the first one.
1. First order differential equations
1.1. Linear inhomogeneous first order differential equation [1], [2], [3]:
![]() . (1.1)
. (1.1)
Logarithmic integration method. In equation (1.1) the function ![]() is not identically zero. Then
is not identically zero. Then ![]() be not identically zero. Then with equation (1.1), consequently we get
be not identically zero. Then with equation (1.1), consequently we get
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]() (1.2)
(1.2)
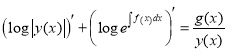 ,
, ![]()
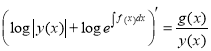 ,
,
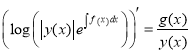 ,
, ![]()
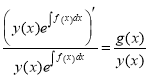 ,
, ![]()
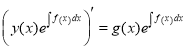 ,
, ![]()
![]() ,
, ![]()
![]() . (1.3)
. (1.3)
Remark 1.1. A similar method can be used to obtain a solution of the equation (1.1) in the Cauchy form [3]:
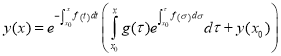 , (1.4)
, (1.4)
where ![]() is a given constant.
is a given constant.
Indeed, the equation (1.2) is equivalent to the equation
![]() , (1.5)
, (1.5)
where
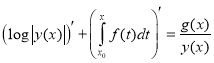 ,
, ![]()
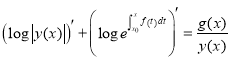 ,
, ![]()
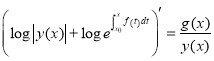 ,
, ![]()
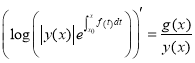 ,
, ![]()
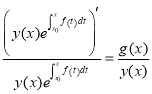 ,
, ![]()
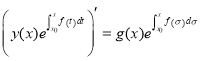 ,
, ![]()
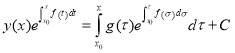 ,
, ![]()
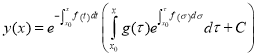 . (1.6)
. (1.6)
If in the equation (1.6) we let ![]() , then we have the formula (1.4).
, then we have the formula (1.4).
1.2. Bernoulli differential equation [3]:
where ![]() .
.
Logarithmic integration method. Let ![]() be not identically zero. Then from the equations (1.7) we obtain
be not identically zero. Then from the equations (1.7) we obtain
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
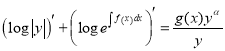 ,
, ![]()
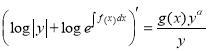 ,
, ![]()
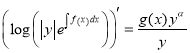 ,
, ![]() (1.8)
(1.8)
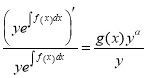 ,
, ![]()
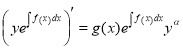 ,
, ![]()
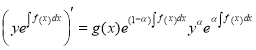 ,
,
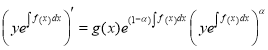 ,
, ![]()
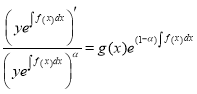 ,
, ![]()
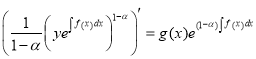 ,
, ![]()
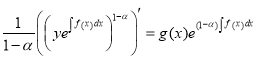 ,
, ![]()
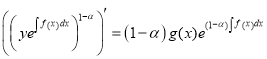 ,
, ![]() (1.9)
(1.9)
![]() ,
, ![]()
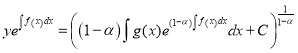 ,
, ![]()
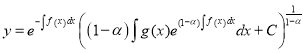 . (1.10)
. (1.10)
Remark 1.2. At the beginning of the course of the method, we assumed that ![]() be not identically zero. It follows that the equation (1.7) has a particular solution
be not identically zero. It follows that the equation (1.7) has a particular solution ![]() , if
, if ![]() .
.
Remark 1.2.1.(The second version of the logarithmic method.) In the equations (1.7) we obtain
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
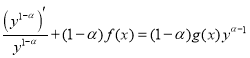 ,
, ![]()
![]() ,
, ![]()
![]() . (1.11)
. (1.11)
The equation (1.11) is a linear inhomogeneous first order differential equation, with respect to the function ![]() . Its solution by the with formula (1.3), has the form
. Its solution by the with formula (1.3), has the form
![]() . (1.12)
. (1.12)
The formula (1.12) implies the solution (1.10).
Remark 1.2.2.(The third version of the logarithmic method.) In the equations (1.8) we obtain
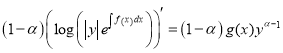 ,
, ![]()
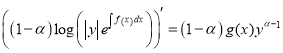 ,
, ![]()
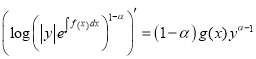 ,
, ![]()
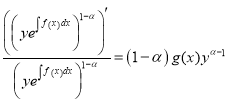 ,
, ![]()
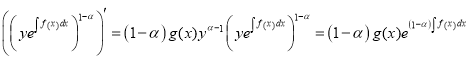 . (1.13)
. (1.13)
The equation (1.13) is similar to the equation (1.9).
1.3. The equation of the form:
![]() , (1.14)
, (1.14)
where ![]() .
.
Logarithmic integration method. From the equation (1.14), we obtain
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
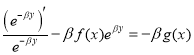 ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() . (1.15)
. (1.15)
The equation (1.15) is a linear inhomogeneous first order differential equation, with respect to the function ![]() . Its solution, by the formula (1.3), has the form
. Its solution, by the formula (1.3), has the form
![]() . (1.16)
. (1.16)
Solving the equation (1.16), with respect to ![]() , we have
, we have
![]() . (1.17)
. (1.17)
Second order differential equation
2.1. Linear homogeneous second order differential equation [1], [3]:
![]() , (2.1)
, (2.1)
where ![]() ,
, ![]() are real numbers.
are real numbers.
Let ![]() be not identically zero. Then from the equations (2.1) we obtain
be not identically zero. Then from the equations (2.1) we obtain
![]() ,
, ![]()
![]() , (2.2)
, (2.2)
because ![]() ,
, 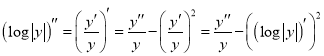 ,
, ![]()
![]() .
.
Let in the equation (2.2):
![]() .
.
Then we have equation (2.2) in the form
![]() ,
, ![]() (2.3)
(2.3)
![]() . (2.4)
. (2.4)
Case 1. ![]() . In this case we have equation (2.4) has be form
. In this case we have equation (2.4) has be form
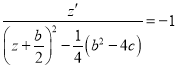 ,
, ![]()
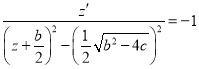 ,
, ![]()
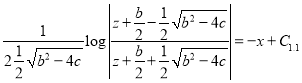 . (2.5)
. (2.5)
Let in the equation (2.5): ![]() ,
, ![]() . Then we obtain
. Then we obtain
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]()
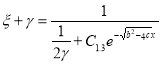 . (2.6)
. (2.6)
Returning to the change of variables ![]() ,
, ![]() , in the equation (2.6), we obtain
, in the equation (2.6), we obtain
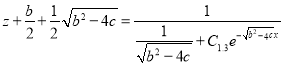 ,
, ![]()
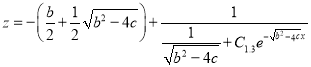 ,
, ![]()
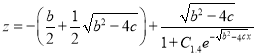 ,
, ![]() ,
, ![]()
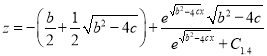 . (2.7)
. (2.7)
Since ![]() , then we have in the equation (2.7)
, then we have in the equation (2.7)
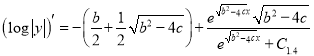 ,
, ![]()
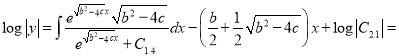
![]() ,
, ![]()
![]() ,
, ![]()
![]() , (2.8)
, (2.8)
where ![]() ,
, ![]() is an integration constant.
is an integration constant.
Case 2. ![]() . In this case we have equation (2.4) has be form
. In this case we have equation (2.4) has be form
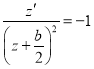 .
.
Step by step from the last equation we obtain
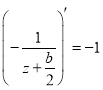 ,
, ![]()
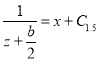 ,
, ![]()
![]() ,
, ![]()
![]() . (2.9)
. (2.9)
Since
![]() ,
, ![]()
![]() ,
, ![]()
![]() , (2.10)
, (2.10)
where ![]() is an integration constant.
is an integration constant.
Case 3. ![]() . In this case we have equation (2.4) has be form
. In this case we have equation (2.4) has be form
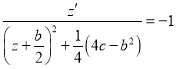 ,
, ![]()
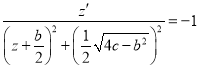 ,
, ![]()
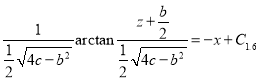 ,
, ![]()
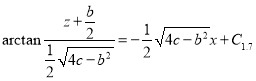 ,
, ![]() ,
, ![]()
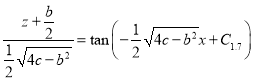 ,
, ![]()
Since ![]() , then we have in the equation (2.11)
, then we have in the equation (2.11)
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]() , (2.12)
, (2.12)
where ![]() ,
, ![]() is an integration constant.
is an integration constant.
The formulas (2.8), (2.10), (2.12) solve the equation (2.1) in the respective cases 1,2,3. This method makes it possible to obtain these solutions without applying a complex analysis and finding a solution in the form ![]() .
.
References:
- C. H. Edwards, D. E. Penny. Differential Equations and Boundary Value Problems: Computing and Modeling (Third Edition), (2010) — 708 p.
2. C. H. Edwards, D. E. Penny, D. Calvis. Elementary differential equations, — 632 p.
3. N. M. Matveev. Metodu integrirovaniya obiknovennih differentsialnih uravneniy, Izdatyelstvo leningradskoho universiteta, (1955) — 655 p.







