В статье рассмотрен пример для выбора лучшей альтернативы с помощью метода анализа иерархий.
Ключевые слова: метод анализа иерархий, ранжирование, матрица суждений.
Исходные данные
Три предприятия (П1, П2 и П3) и список ранжированных критериев.
Таблица 1
|
№ |
Критерий |
Предприятия |
||
|
П1 |
П2 |
П3 |
||
|
1 |
Уровень доходов (млн. руб/год) |
640 |
600 |
800 |
|
2 |
Эксплуатационные затраты (млн. руб/год)* |
80 |
45 |
70 |
|
3 |
Использование информационных технологий аппаратом управления (число автоматизир. фун.) |
15 |
10 |
30 |
|
4 |
Объем продаж (млн. руб/год) |
200 |
180 |
250 |
|
5 |
Уровень производственного травматизма (случ./год)* |
30 |
50 |
40 |
|
6 |
Уровень шума (дб)* |
150 |
180 |
220 |
|
7 |
Экономический риск (вероятность в %)* |
21 |
15 |
30 |
|
8 |
Уровень инновационной деятельности (в баллах) |
6 |
7 |
8 |
|
9 |
Уровень капиталовложений (млн. руб/год)* |
200 |
300 |
600 |
|
10 |
Уровень загрязнения воды (% примесей)* |
2 |
4 |
2 |
|
11 |
Уровень загрязнения воздуха (% примесей)* |
6 |
8 |
7 |
Применение метода анализа иерархий.
Иерархия структуры системы предназначена для изучения функциональных взаимодействий ее компонент и их воздействий на систему в целом. Оценка вариантов решений методом анализа иерархий сводится к следующему:
- Систему представим в виде иерархии, которая изображается графом связей между элементами уровней. Можно построить следующую иерархию (рис. 1).
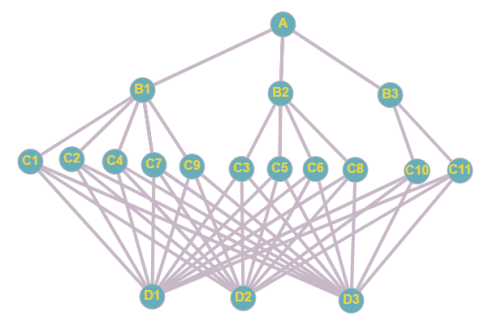
Рис. 1. Иерархия
На рисунке 1 буквами буквой A обозначен нулевой уровень иерархии, В обозначены виды критериев (показателей) предприятия, буквыСобозначают конкретные критерии, буквы D — сами предприятия.
А. Глобальный критерий (цель) системы — эффективность работы предприятия.
В1. Экономические показатели
С1. Уровень доходов (млн. руб./год)
С2. Эксплуатационные затраты (млн. руб./год)
С4. Объем продаж (млн. руб./год)
С7. Экономический риск (вероятность в %)
С9. Уровень капиталовложений (млн. руб./год)
В2. Производственные показатели
С3. Использование информационных технологий аппаратом управления (чисто автоматизир. фун.)
С5. Уровень производственного травматизма (случ./год)
С6. Уровень шума (дб)
С8. Уровень инновационной деятельности (в баллах)
В3. Охрана окружающей среды
С10. Уровень загрязнения воды (% примесей)
С11. Уровень загрязнения воздуха (% примесей)
Предприятия
D1. Предприятие № 1
D2. Предприятие № 2
D3. Предприятие № 3
- Составим матрицы парных сравнений (суждений или приоритетов). Для парных сравнений использовалась 9-балльная шкала Т. Саати, причем для каждой матрицы считается индекс согласованности, интервал для которого [0:0,15]:
Таблица 2
Первый уровень
|
A |
AB1 |
AB2 |
AB3 |
∑ |
Пi |
ИС |
|
AB1 |
1,00 |
3,00 |
5,00 |
9,00 |
0,61 |
0,06 |
|
AB2 |
0,33 |
1,00 |
3,00 |
4,33 |
0,29 |
|
|
AB3 |
0,20 |
0,33 |
1,00 |
1,53 |
0,10 |
Второй уровень
|
B1 |
B1C1 |
B1C2 |
B1C4 |
B1C7 |
B1C9 |
∑ |
Пi |
ИС |
|
B1C1 |
1,00 |
2,00 |
3,00 |
2,00 |
0,33 |
8,33 |
0,23 |
0,13 |
|
B1C2 |
0,50 |
1,00 |
0,25 |
2,00 |
0,25 |
4,00 |
0,11 |
|
|
B1C4 |
0,33 |
3,00 |
1,00 |
3,00 |
1,00 |
8,33 |
0,23 |
|
|
B1C7 |
0,50 |
0,50 |
0,33 |
1,00 |
0,25 |
2,58 |
0,07 |
|
|
B1C9 |
3,00 |
4,00 |
1,00 |
4,00 |
1,00 |
13,00 |
0,36 |
|
|
B2 |
B2C3 |
B2C5 |
B2C6 |
B2C8 |
∑ |
Пi |
ИС |
|
|
B2C3 |
1,00 |
2,00 |
3,00 |
1,00 |
7,00 |
0,28 |
0,12 |
|
|
B2C5 |
0,50 |
1,00 |
0,33 |
0,20 |
2,03 |
0,08 |
||
|
B2C6 |
0,33 |
3,00 |
1,00 |
0,25 |
4,58 |
0,19 |
||
|
B2C8 |
1,00 |
5,00 |
4,00 |
1,00 |
11,00 |
0,45 |
||
|
B3 |
B3C10 |
B3C11 |
∑ |
Пi |
ИС |
|
||
|
B3C10 |
1,00 |
2,00 |
3,00 |
0,67 |
0,00 |
|||
|
B3C11 |
0,50 |
1,00 |
1,50 |
0,33 |
- Из векторов приоритетов, оценивающих влияние элементов i+1-го уровня на каждый связанный с ним элемент i-го уровня, образуем матрицу приоритетов, которая умножается справа на вектор приоритетов полученный на i-м уровне иерархии и получается вектор приоритетов i+1-го уровня.
Таблица 3
Матрица приоритетов второго уровня, умноженная на вектор приоритетов первого уровня
|
|
B1 |
B2 |
B3 |
|
|||
|
C1 |
0,23 |
0,00 |
0,00 |
0,14 |
|||
|
C2 |
0,11 |
0,00 |
0,00 |
0,07 |
|||
|
C3 |
0,00 |
0,28 |
0,00 |
0,08 |
|||
|
C4 |
0,23 |
0,00 |
0,00 |
0,61 |
0,14 |
||
|
C5 |
0,00 |
0,08 |
0,00 |
* |
0,29 |
= |
0,02 |
|
C6 |
0,00 |
0,19 |
0,00 |
0,10 |
0,05 |
||
|
C7 |
0,07 |
0,00 |
0,00 |
0,04 |
|||
|
C8 |
0,00 |
0,45 |
0,00 |
0,13 |
|||
|
C9 |
0,36 |
0,00 |
0,00 |
0,22 |
|||
|
C10 |
0,00 |
0,00 |
0,67 |
0,07 |
|||
|
C11 |
0,00 |
0,00 |
0,33 |
0,03 |
- После этого шага составляется 11 матриц сужений (по числу критериев) приоритетов вариантов разработки месторождений:
Третий уровень
|
C1 |
C1D1 |
C1D2 |
C1D3 |
∑ |
Пi |
ИС |
|
C6 |
C6D1 |
C6D2 |
C6D3 |
∑ |
Пi |
ИС |
|
C1D1 |
1,00 |
2,00 |
0,33 |
3,33 |
0,29 |
0,09 |
C6D1 |
1,00 |
0,50 |
1,00 |
2,50 |
0,25 |
0,11 |
|
|
C1D2 |
0,50 |
1,00 |
0,50 |
2,00 |
0,18 |
C6D2 |
2,00 |
1,00 |
0,50 |
3,50 |
0,35 |
|||
|
C1D3 |
3,00 |
2,00 |
1,00 |
6,00 |
0,53 |
C6D3 |
1,00 |
2,00 |
1,00 |
4,00 |
0,40 |
|||
|
C2 |
C2D1 |
C2D2 |
C2D3 |
∑ |
Пi |
ИС |
|
C7 |
C7D1 |
C7D2 |
C7D3 |
∑ |
Пi |
ИС |
|
C2D1 |
1,00 |
1,00 |
0,50 |
2,50 |
0,26 |
0,03 |
C7D1 |
1,00 |
0,50 |
2,00 |
3,50 |
0,35 |
0,11 |
|
|
C2D2 |
1,00 |
1,00 |
1,00 |
3,00 |
0,32 |
C7D2 |
2,00 |
1,00 |
1,00 |
4,00 |
0,40 |
|||
|
C2D3 |
2,00 |
1,00 |
1,00 |
4,00 |
0,42 |
C7D3 |
0,50 |
1,00 |
1,00 |
2,50 |
0,25 |
|||
|
C3 |
C3D1 |
C3D2 |
C3D3 |
∑ |
Пi |
ИС |
|
C8 |
C8D1 |
C8D2 |
C8D3 |
∑ |
Пi |
ИС |
|
C3D1 |
1,00 |
0,25 |
0,33 |
1,58 |
0,12 |
0,03 |
C8D1 |
1,00 |
3,00 |
0,33 |
4,33 |
0,29 |
0,06 |
|
|
C3D2 |
4,00 |
1,00 |
2,00 |
7,00 |
0,54 |
C8D2 |
0,33 |
1,00 |
0,20 |
1,53 |
0,10 |
|||
|
C3D3 |
3,00 |
0,50 |
1,00 |
4,50 |
0,34 |
C8D3 |
3,00 |
5,00 |
1,00 |
9,00 |
0,61 |
|||
|
C4 |
C4D1 |
C4D2 |
C4D3 |
∑ |
Пi |
ИС |
|
C9 |
C9D1 |
C9D2 |
C9D3 |
∑ |
Пi |
ИС |
|
C4D1 |
1,00 |
4,00 |
0,50 |
5,50 |
0,42 |
0,09 |
C9D1 |
1,00 |
3,00 |
0,50 |
4,50 |
0,40 |
0,09 |
|
|
C4D2 |
0,25 |
1,00 |
0,33 |
1,58 |
0,12 |
C9D2 |
0,33 |
1,00 |
0,50 |
1,83 |
0,16 |
|||
|
C4D3 |
2,00 |
3,00 |
1,00 |
6,00 |
0,46 |
C9D3 |
2,00 |
2,00 |
1,00 |
5,00 |
0,44 |
|||
|
C5 |
C5D1 |
C5D2 |
C5D3 |
∑ |
Пi |
ИС |
|
C10 |
C10D1 |
C10D2 |
C10D3 |
∑ |
Пi |
ИС |
|
C5D1 |
1,00 |
3,00 |
2,00 |
6,00 |
0,53 |
0,09 |
C10D1 |
1,00 |
4,00 |
0,50 |
5,50 |
0,42 |
0,09 |
|
|
C5D2 |
0,33 |
1,00 |
2,00 |
3,33 |
0,29 |
C10D2 |
0,25 |
1,00 |
0,33 |
1,58 |
0,12 |
|||
|
C5D3 |
0,50 |
0,50 |
1,00 |
2,00 |
0,18 |
C10D3 |
2,00 |
3,00 |
1,00 |
6,00 |
0,46 |
|
C11 |
C11D1 |
C11D2 |
C11D3 |
∑ |
Пi |
ИС |
|
C11D1 |
1,00 |
1,00 |
0,50 |
2,50 |
0,25 |
0,11 |
|
C11D2 |
1,00 |
1,00 |
2,00 |
4,00 |
0,40 |
|
|
C11D3 |
2,00 |
0,50 |
1,00 |
3,50 |
0,35 |
- Далее из 11 полученных векторов столбцов приоритетов формируется матрица приоритетов третьего уровня иерархии, которая умножается на вектор приоритетов, полученный на предыдущем шаге, и получается вектор приоритетов предприятий:
Таблица 4
Матрица приоритетов второго уровня, умноженная на вектор приоритетов первого уровня
|
0,14 |
||||||||||||||||
|
0,07 |
||||||||||||||||
|
0,08 |
||||||||||||||||
|
|
C1 |
C2 |
C3 |
C4 |
C5 |
C6 |
C7 |
C8 |
C9 |
C10 |
C11 |
|
0,14 |
Место: |
||
|
D1 |
0,29 |
0,26 |
0,12 |
0,42 |
0,53 |
0,25 |
0,35 |
0,29 |
0,40 |
0,42 |
0,25 |
0,02 |
0,33 |
II |
||
|
D2 |
0,18 |
0,32 |
0,54 |
0,12 |
0,29 |
0,35 |
0,40 |
0,10 |
0,16 |
0,12 |
0,40 |
* |
0,05 |
= |
0,22 |
III |
|
D3 |
0,53 |
0,42 |
0,34 |
0,46 |
0,18 |
0,40 |
0,25 |
0,61 |
0,44 |
0,46 |
0,35 |
0,04 |
0,45 |
I |
||
|
0,13 |
||||||||||||||||
|
0,22 |
||||||||||||||||
|
0,07 |
||||||||||||||||
|
0,03 |
Результаты метода анализа иерархий:
Предприятие 3 занимает первое место (лучшее);
Предприятие 1 занимает второе место;
Предприятие 2 занимает третье место.
Литература:
- Степин Ю. П. Компьютерная поддержка формирования, многокритериального ранжирования и оптимизации управленческих решений в нефтегазовой отрасли: Учеб. пособие. — М.: ООО «Издательский дом недра», 2016. — 421 с.: ил.
- Костевич Л. С., Лапко А. А. Исследование операций. Теория игр. — Минск: Вышейная школа, 2008. — 368 с.
- Евланов Л. Г. Теория и практика принятия решений. — М.: Экономика, 1984. — с. 176







