Уменьшение невозмущаемых колебаний инерциальных систем путём корректирующего введения внешней информации



Рассмотрен метод коррекции невозмущаемых колебаний инерциальной системы от источника внешней информации. При моделировании упрощённой инерциальной системы оценена возможность уменьшения периода невозмущаемых колебаний и коррекции инструментальных погрешностей от сигналов внешней информации, обрабатываемых встроенным вычислительным устройством.

Ключевые слова: инерциальная система, коррекция, корректирующее введение, информация, возмущение, акселерометр, гироскоп.

Инерциально-навигационные системы в настоящее время широко применяются в системах управления баллистических ракет, самолётов, морских кораблей и других подвижных объектов [1–3]. Основы теории инерциальных методов определения параметров движения различных объектов, теория невозмущённого и возмущённого функционирования инерциальных навигационных и навигационно-пилотажных систем изложены в ряде научно-исследовательских работ [3–7].

Для улучшения статических и динамических характеристик современных инерциально-навигационных систем, повышения помехозащищённости и надёжности функционирования, автоматизирования процессов обмена информации и также обеспечения взаимной компенсации и фильтрации погрешностей, в их составе обычно входят два, даже три навигационных устройства, основанных на различных методах измерения. К ним относятся работы [6–12]. Инструментальные погрешности инерциальной системы, так же как и не точности начальной установки гироскопа и акселерометра, вызывают незатухающие колебания с периодом невозмущаемости или близким к нему. Эти колебания создают от начальных нежелательные смещения по трём осям ориентации платформы инерциальной системы, что увеличивают погрешности показаний скорости и координат. Проблема уменьшения таких нежелательных колебаний и также погрешности временно-накапливания погрешностей с течением времени в инерциальных системах решается в ряде работ [11–15].

В настоящей статье при моделировании упрощённой инерциальной системы, состоящей из гироскопа вертикали, акселерометра и вычислительных устройств (первичного и вторичного интеграторов), обеспечивающей определения скорости и пройдённого вдоль ортодромии пути [16–18] обоснована возможность уменьшения невозмущаемых колебаний и коррекции инструментальных погрешностей от корректирующих сигналов внешней информации.

Использование метода коррекции от внешней информации для уменьшения невозмущаемых колебаний инерциальных систем

Корректирующая внешняя информация полезна для уменьшения возмущений инерциальной системы, получающихся при введении в неё демпфирования, и может служить для сокращения периода невозмущаемых колебаний системы. Уменьшение этих погрешностей, вызываемых демпфированием, осуществляется за счёт так называемой внешней информации, т. е. за счёт внесения коррекции в демпфирующий сигнал от источников информации, не связанных с самой инерциальной системой. Возможность уменьшения периода невозмущаемых колебаний гироскопических систем с введением в них демпфирования было указано во многих работах [7–10]. А применительно к инерциальным системам это, по-видимому, тоже было описано в ряде литератур [11–18].

Рассмотрим простую инерциальную систему, ориентированную вдоль какой-либо ортодромии и перпендикулярна к ней (рис 1.). В этой системе информационный сигнал о скорости, регистрируя чувствительными элементами (гироскопом и акселерометром), проходя различные преобразования и обработки (первый и второй интегратор), выходит и в указатели выходной информации либо в другие исполнительные узлы.

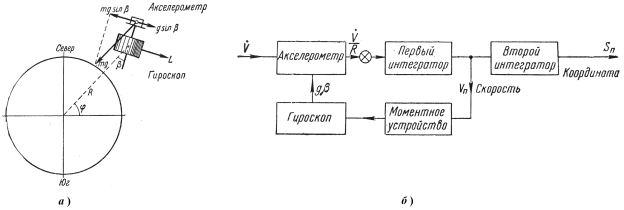
Рис. 1. Иллюстрация (а) и структурная схема (б) рассмотренной инерциальной системы

Отметим, что использование сигналов, проходящих через различные цепи измерительной схемы, особенно содержащие дифференцирующие и интегрирующие функции, даёт возможность получить на выходе данные не только об основном параметре, но и об его производных или интегралах во времени, а также другие функциональные зависимости, необходимые для навигации и управления. В общем случае полезный входной сигнал может иметь сложную структуру (спектры амплитуд, частот, фаз, скоростей распространения), компоненты которой являются определёнными функциями навигационных параметров объекта. При применении в инерциальной системе вспомогательных фильтров, позволяющих выделить эту информацию и представить ее в виде исходных сигналов. Поэтому обнаружение сигнала помехи и выявление его информационного содержания, т. е. об изменении внешних условий, о работе источников помех (естественных и искусственных), может быть использовано для ограничения вредного воздействия самих помех, для перехода на другие режимы измерения и перестройки контуров схемы обратной связи, для включения других измерительных устройств, использующих сигналы помехи в качестве полезного сигнала [16–18]. С этой точки зрения в цепи коррекции проходят сигналы, характеризующие различные виды погрешностей. Обработка этих сигналов позволяет установить их основные статистические характеристики и обеспечить более эффективную коррекцию погрешностей [19–20].

В рамках этой статьи не будем моделировать и рассматривать все составляющие погрешности, влияющие на инерциальные системы, а лишь исследуем метод коррекции невозмущаемых колебаний от внешней информации в упрощённой схемы системы. Допустим, что в течение некоторого времени на летательном аппарате можно получать сведения от какого-либо внешнего источника информации о координате и путевой скорости, удобны для введения в рассмотренную упрощённую систему (рис. 2). Будем полагать, что эти сведения достаточно точны, а в показаниях инерциальной системы инструментальные погрешности столь малы, что ими можно пренебречь. В этом случае погрешности инерциальной системы будут зависеть только от несовпадения гировертикали (или платформы во второй схемы моделирования) с вертикалью места (горизонтом), вследствие чего будут иметь место колебания [9–13].

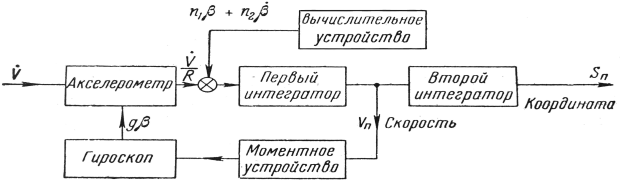
Рис. 2. Структурная схема инерциальной системы с использованием корретирующей информации от внешнего источника

Если показания инерциальной системы дают, например, для пройдённого вдоль ортодромии пути величину S_п, а сведения, полученные от внешнего источника информации, дают S, то разность S — S_п, даст погрешность инерциальной системы:

, (1)

где R — величина радиуса Земли (при пренебрежении высотой оси инерциальной системы над поверхностью Земли), β — относительный угол поворота (относительно вертикального направления).

Отсюда

, (2)

Вычислив таким образом β, подадим дополнительно на первый интегратор эту величину, умноженную на коэффициент n1.

Далее аналогично предыдущему найдём величину β·:

, (3)

где V — путевая скорость, полученная от источников внешней информации, Vп — показание путевой скорости, выданное инерциальной системы.

Поступим с β· так же, как и с величиной β, т. е. подадим на первый интегратор ещё и значение вычисленной величины β·, умноженной на коэффициент n2. При этом, сигнал коррекции ζ от внешней информации, обрабатываемый в вычислительном устройстве и поступающий в схему инерциальной системы, может быть сформулирован:

, (4)

Таким образом, уравнение гировертикали будет иметь вид:

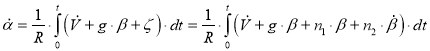, (5)

где α — угол отклонения оси гироскопа от вертикального направления, t — время движения, φ = α + β — угол поворота вертикали, g — величина гравитационного ускорения, V — линейная скорость движения инерциальной системы, R — величина радиуса Земли (при пренебрежении высотой оси инерциальной системы над поверхностью Земли), k — коэффициент пропорциональности.

С учётом условий α·= φ· — β·, φ·= V / R получено следующее уравнение:

. (6)

Предполагается, что при нормальном режиме работы рассмотренной инерциальной системы коэффициенты n1, n2 могут быть считать медленно меняющимися, т. е. при кратковременном использовании системы они остаются постоянными. При этом, уравнением (5) является однородной дифференциальной функцией второго порядка с постоянными коэффициентами. В общем случае, общим решением уравнения (6) является следующая функция:

, (7)

где A, B — коэффициенты, зависящие от начальных условий системы, β1(t), β2(t) — фундаментальная система решений уравнения (6), представляющая собой систему линейно независимых решением. Кратко критерий линейной независиомсти может быть сформулирован следующим образом: функции β1(t), β2(t) является линейно независимыми, если определитель Вронского (вронскианом)

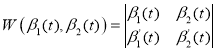, (8)

отличен от нуля для любого интервала времени t.

Л. Эйлером была предложена фундаментальная система решений такого уравнения β1(t), β2(t), описывающая в виде β(t) =ekt. В зависимости от корней характеристического уравнения выделяются частные решения (соответствующие корням характеристического уравнения), образующие фундаментальную систему решений и записывается соответствующее общее решение (7). И так:

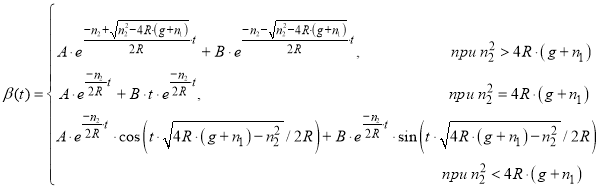.(9)

Качество использования метода коррекции от внешней информации сильно зависит от каких значений коэффициентов, регулированных вычислительном устройством. Для улучшения качества коррекции оптимальные такие коэффициенты должны выбраны, исходя из технических требований реализации инерциальной системы. Если достаточно велико, то собственный период системы Tc=2π·√(R/(g+n1)) может быть сделан значительно меньшим периода М.Шулера, т. е. меньше 84,4 мин (для поверхности Земли). В то же время система имеет демпфирование, причём введение сигнала по вычислительному значению β· в первый интегратор осуществляет это демпфирование, не вводя в систему возмущений. Таким образом, наличие внешней информации даёт возможность демпфировать колебания в инерциальной системе без введения в неё возмущения и сокращать период собственных системы, не нарушая свойство невозмущаемости. При этом, использование коррекции от внешней информации может оказаться весьма полезным, так как за сравнительно короткий промежуток времени можно осуществить демпфирование колебаний, обусловленных начальными ошибками системы.

Известны и популярны в современной технике способы коррекции инерциальных систем с использованием данных от внешних источников информации, в качестве которых могут выступать данные от систем GPS, ГЛОНАСС, Galileo, систем навигации по геофизическим полям, систем навигации по картам местности и др. При этом от таких приёмников непрерывно осуществляются получение данных о временном местоположении объекта, сравнение этих данных с параметрами, выработанными инерциальной системы, и вычисление по результатам сравнения поправок к выходным параметрам инерциальной системы и сигналов, обеспечивающих устранение погрешностей чувствительных элементов (гироскопов и акселерометров).

Выводы

Обсуждён метод коррекции от внешней информации для уменьшения невозмущаемых колебаний инерциальной системы. При моделировании упрощённой инерциальной системы оценена возможность уменьшения периода невозмущаемых колебаний и коррекции инструментальных погрешностей от сигналов внешней информации, обрабатываемых вычислительным устройством. Такой способ коррекции в большинстве случае улучшает характеристики инерциальных систем, и также уменьшает их дополнительные погрешности, обеспечивает широкую возможность применения таких систем в ряде области современной техники. Хотя бы, потребуются дополнительные измерительно-приемоиндикаторные оборудования внешней информации, исполнительные узлы… и также к сожалению, делает инерциальную систему не полностью автономной. При этом появляется усложнение при проектировании навигационной системы для самолётов-разведчиков, необходимых автономное решение целевой задачи, или для летательных аппаратов, судов и др., на которых должно обеспечивать приемлемое качество определения навигационных параметров в условиях автономного управления, когда сигналы с внешних корректирующих систем недоступны. Следовательно, оптимальным решением оказывается какой метод, зависящий от технических требований исследования и разработки конкретных инерциальных систем.

Литература:

1. Пешехонов В. Г. Ключевые задачи современной автономной навигации // Гироскопия и навигация. 1996. № 1(12). с. 48–55.
2. Браславский Д. А. Приборы и датчики летательных аппаратов. М.: Машиностроение, 1970. — 392 с.
3. Помыкаев И. И. Селезнев В. П., Дмитроченко Л. А. Навигационные приборы и системы. М.: Машиностроение, 1983. — 456 с.
4. Лебедев, Р. К. Стабилизация летательного аппарата бесплатформенной инерциальной системой. М.: Машиностроение, 1977. — 144 с.
5. Савинов Г. Ф., Гора В. П., Дмитроченко, Л. А. Бесплатформенные инерциальные навигационные системы. М.: МАИ, 1984. — 64 с.
6. Бромберг П. В. Теория инерциальных систем навигации. М.: Наука, 1979. — 291 с.
7. Красильщиков М. Н., Себряков Г. Г. Управление и наведение беспилотных манёвренных летательных аппаратов на основе современных информационных технологий. М.: Физматлит, 2003. — 280 с.
8. Бранец В. Н., Шмыглевский И. П. Введение в теорию бесплатформенных инерциальных навигационных систем. М.: Наука, 1992. — 410 с.
9. Зельдович С. М., и др. Автокомпенсация инструментальных погрешностей гиросистем. -Ленинград: Судостроение, 1976. — 255 с.
10. Ahmad N., Ghazilla R., Khairi N. M., Kasi V. Reviews on various inertial measurement unit (IMU) sensor applications // International Journal of Signal Processing Systems. 2013, vol 1(2). 256–262 pp.
11. Фам А. Т., Нгуен В. Т., Нгуен В. Т. К вопросу о демпфировании невозмущаемых колебаний в автономных инерциальных системах // Молодой учёный. 2019, № 10, — c. 27–30.
12. G. F. Franklin, J. D. Powell, A. Emami-Naeini. Feedback control of dynamic systems. Menlo Park, CA: Addison Wesley, 4^th ed., 2002.
13. Боднер В. А. и др. К теории инерциальных демпфированных систем с произвольным периодом, инвариантных по отношению к маневрированию объекта // Известия АН СССР, ОТН, Энергетика и автоматика, № 3, 1959.
14. Андреев В. Д. Теория инерциальной навигации: автономные системы. — М.: Наука, 1966.
15. Rao A. V. Dynamics Теория инерциальной навигации: автономные системы. — М.: Наука, 1966.
16. M. S. Grewal, L. R. Weill, A. P. Andrews. Global positioning systems, inertial-navigation, and integration. New Jersey: John Wiley & Sons, 2^nd ed., 2007.
17. D. A. Tazartes. Inertial navigation: from gimbaled platforms to strap-down sensors // IEEE Transactions on Aerospace and Electronic Systems. 2011. vol 47 (3), 2292–2299 pp.
18. Salychev O. S. Applied Inertial Navigation. Problems and Solutions. М.: Pub: BMSTU, 2004. — 320 pp.
19. Лысенко Л. Н. Наведение и навигация баллистических ракет. М.: Изд-во МГТУ им. Н. Э. Баумана, 2007. — 669 с.
20. Рэндал У. Б., Тимоти У. М. Л. Малые беспилотные летательные аппараты: теория и практика. М.: ТЕХНОСФЕРА, 2015. — 312 с.