Рассматривается задача разбиения многосвязного ортогонального полигона на прямоугольные области. Критерием оптимизации является минимизация протяженности стыков между прямоугольниками, образующими разбиение. Предложена модификация модели Бизли для решения рассматриваемой задачи. Рассмотрено сведение исходных данных задачи к структуре модифицированной модели Бизли. Предложен алгоритм поиска оптимального разбиения методами линейного программирования.
Ключевые слова: разбиение многосвязного ортогонального полигона, минимизация протяженности стыков, декомпозиция полигона, модель Бизли, линейное программирование
Введение
В настоящее время в различных открытых источниках описано множество способов нахождения разбиения односвязного ортогонального полигона с минимизацией протяженности стыков или многосвязного ортогонального полигона с минимизацией количества простых фигур в качества критерия оптимизации. Известны также способы рекурсивной обработки многосвязного ортогонального полигона, некоторым образом, представимого в виде совокупности односвязных ортогональных полигонов, которые подлежат разбиению. При этом остается открытым вопрос о поиске оптимального решения задачи разбиения исходного многосвязного ортогонального полигона на прямоугольники с минимизацией протяженности стыков. В то же время эта задача является актуальной, поскольку встречается в различных отраслях деятельности человека — в судостроении, строительстве, а также в некоторых других материалоемких отраслях. Суть задачи в том, что необходимо покрыть некоторую область, заданную ортогональным полигоном, набором прямоугольных элементов. При этом:
− исходная область, подлежащая покрытию прямоугольниками (разбиению на прямоугольники), может содержать препятствия (на практике это могут быть колонны, стены, и т. д.), поэтому в общем случае исходный разбиваемый ортогональный полигон считается многосвязным (МОП, многосвязный ортогональный полигон);
− прямоугольные элементы не должны перекрываться между собой и с препятствиями;
− прямоугольные элементы должны покрывать всю полезную площадь исходной области МОП.
Стыком между двумя прямоугольными элементами разбиения будем называть часть общего ребра двух прямоугольных элементов разбиения. Нередко на практике именно такие стыки подлежат дорогостоящей обработке — например, герметизации. Исходя из этих соображений, имеет смысл направлять целевую функцию на минимизацию суммарной протяженности стыков в разбиении МОП. В английском сегменте задача разбиения МОП с минимизацией протяженности стыков называется Minimum Edge Length Partitioning of Rectilinear Polygons with Interior Holes.
Задача эта является частным случаем задач геометрического покрытия. Важным признаком для определения алгоритмической сложности задач такого рода является многосвязность исходного МОП: в случае односвязного МОП задача имеет полиномиальную сложность, в противном случае задача является NP-трудной (даже если препятствия представлены в виде точек, через которые должна пройти хотя бы одна сторона простой фигуры) [1]. Ввиду неполиномиальной сложности алгоритмов решения таких задач, авторами многих работ уделяется значительное внимание различным упрощениям и приближенным методам.
Цель
Целью данной статьи является разработка точного алгоритма для решения задачи разбиения многосвязного ортогонального полигона на прямоугольные непересекающиеся области с минимизацией протяженности стыков между ними.
Для достижения поставленной цели были выделены следующие задачи:
1) Выбрать математическую модель и метод решения задачи.
2) Разработать алгоритм решения задачи на основе выбранного метода решения.
Постановка задачи разбиения МОП с минимизацией протяженности стыков
Имеется многосвязный ортогональный полигон ![]() , где
, где ![]() — множество вершин полигона,
— множество вершин полигона, ![]() — множество препятствий, заданных координатами верхней левой и правой нижней вершин (Рис.1).
— множество препятствий, заданных координатами верхней левой и правой нижней вершин (Рис.1).
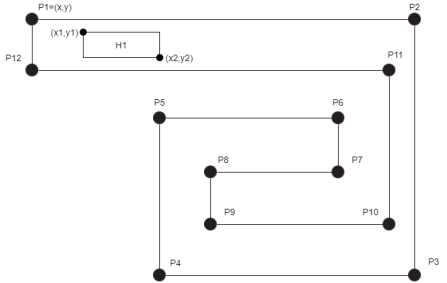
Рис.1. Описание модели
Препятствия могут пересекаться между собой, лежать как снаружи (дополняя МОП до описывающего его прямоугольника), так и внутри полигона.
Необходимо найти разбиение исходного полигона на непересекающиеся прямоугольные области с минимальной протяженностью стыков между ними.
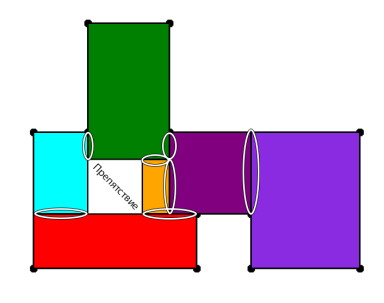
Рис.2. Иллюстрация понятия «препятствие», «стык»
Может также появится заблуждение, что разбиение с минимальной протяженностью стыков достигается при использовании минимально возможного количества простых фигур. В процессе анализа данной задачи, было обнаружено, что это не всегда так (Рис.3, Рис.4). На рисунках ниже приведен пример, когда для одного и того же МОП получены два различных разбиения, одно из которых содержит меньшее количество простых фигур (Рис.3), другое — меньшую суммарную протяженность стыков (Рис.4). Следовательно, критерии минимизации простых фигур в разбиении и минимизации суммарной протяженности стыков не являются эквивалентными.

Рис. 3. Минимизация количества простых фигур. 5 простых фигур, длина стыков — 17

Рис. 4. Минимизация протяженности стыков. 7 простых фигур, длина стыков — 8
Модификация модели Бизли
Образуем множества ![]() и
и ![]() , содержащие в себе
, содержащие в себе ![]() и
и ![]() координаты МОП и препятствий соответственно. И пусть
координаты МОП и препятствий соответственно. И пусть ![]() — это все возможные точки растровой сетки.
— это все возможные точки растровой сетки.
В случае ортогонального полигона и прямоугольных препятствий, все простые фигуры, образующие оптимальное разбиение, содержат в себе точки из множества ![]() . Так как это упрощение не влияет на полученный результат, будет разумно использовать его в нашей модели.
. Так как это упрощение не влияет на полученный результат, будет разумно использовать его в нашей модели.
![]() — множество всех возможных непересекающихся прямоугольников, координаты вершин которых принадлежат множеству
— множество всех возможных непересекающихся прямоугольников, координаты вершин которых принадлежат множеству ![]() , причем точка k расположена правее и ниже точки j.
, причем точка k расположена правее и ниже точки j.
Из
![]()
Заметим, что, так как множество ![]() состоит из непересекающихся прямоугольников, образованных из всех возможных координат
состоит из непересекающихся прямоугольников, образованных из всех возможных координат ![]() и
и ![]() , то ситуация, когда сторона полигона проходит «внутри» прямоугольника
, то ситуация, когда сторона полигона проходит «внутри» прямоугольника ![]() невозможна.
невозможна.
Сформируем множество ![]() всех возможных прямоугольников с координатами из
всех возможных прямоугольников с координатами из ![]() , кроме тех, которые пересекаются хотя бы с одним прямоугольником из
, кроме тех, которые пересекаются хотя бы с одним прямоугольником из ![]() . Опять же, точка k должна быть расположена правее и ниже точки j. Заметим также, что прямоугольники из
. Опять же, точка k должна быть расположена правее и ниже точки j. Заметим также, что прямоугольники из ![]() могут пересекаться.
могут пересекаться.
![]()
Для удобства введем функцию ![]() , определяющую все прямоугольники из
, определяющую все прямоугольники из ![]() , которым принадлежит точка с координатами
, которым принадлежит точка с координатами ![]() и
и ![]() . Будем считать, что что точка принадлежит прямоугольнику, если она лежит внутри него или на его левой или верхней границе (Рис.5).
. Будем считать, что что точка принадлежит прямоугольнику, если она лежит внутри него или на его левой или верхней границе (Рис.5).
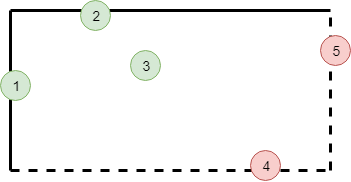
Рис.5. Точки 1,2,3 принадлежат прямоугольнику, а точки 4 и 5 — нет
Образуем множество «хороших» точек ![]() , удалив из
, удалив из ![]() все точки, которые принадлежат препятствиям, или хотя бы одному прямоугольнику из
все точки, которые принадлежат препятствиям, или хотя бы одному прямоугольнику из ![]() , или не принадлежат ни одному из прямоугольников (например, правая нижняя точка модели).
, или не принадлежат ни одному из прямоугольников (например, правая нижняя точка модели).
![]()
Лемма 1: если для произвольной точки ![]() выбрать только один прямоугольник из
выбрать только один прямоугольник из ![]() , значит эта точка покрыта только один раз (прямоугольники не пересекаются).
, значит эта точка покрыта только один раз (прямоугольники не пересекаются).
Лемма 2: если для всех точек из
Переход к модели линейного программирования
Введем переменную ![]() , обозначающую, используем ли мы прямоугольник i из
, обозначающую, используем ли мы прямоугольник i из ![]() в разбиении.
в разбиении. ![]() если прямоугольник используется и
если прямоугольник используется и ![]() в противном случае.
в противном случае.
Протяженность стыков — это суммарный периметр всех прямоугольников полученного разбиения минус ![]() пополам, где
пополам, где ![]() — сумма периметра полигона и периметра препятствий, причем периметр препятствий может быть отрицательным.
— сумма периметра полигона и периметра препятствий, причем периметр препятствий может быть отрицательным.
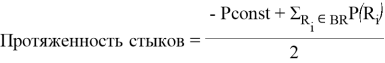
Таким образом, функция цели: ![]() , где
, где ![]() — периметр прямоугольника
— периметр прямоугольника ![]() .
.
Для каждой точки из ![]() запишем ограничение:
запишем ограничение: ![]() — в разбиении должен использоваться только один прямоугольник из тех, которыми можно покрыть эту точку.
— в разбиении должен использоваться только один прямоугольник из тех, которыми можно покрыть эту точку.
В результате решения этой модели симплексным методом станут известны значения всех ![]() . Совокупность прямоугольников
. Совокупность прямоугольников ![]() , таких что
, таких что ![]() , образует оптимальное разбиение исходной области МОП.
, образует оптимальное разбиение исходной области МОП.
Выводы
Разработана модификация существующей модели Бизли для представления исходных данных задачи разбиения многосвязного ортогонального полигона, а также предложена новая функция цели для нахождения разбиения с минимальной протяженностью стыков средствами линейного программирования. Достоинством данного алгоритма является возможность нахождения точного решения. Главный недостаток — время решения, которое растет вместе с увеличением размерности задачи. Тем не менее, данный алгоритм пригоден для случаев, когда нахождение точного результата важнее времени его расчёта.
Литература:
- Lingas A., Pinter R. Y., Rivest R. L., Shamir A., Minimum edge length partitioning of rectilinear polygons, Proc. 20th Allerton Conf. Comput., 1982, с. 53–63
- Teofilo F. Gonzales Handbook of Approximation Algorithms and Metaheuristics — Taylor & Francis LLC, 2007, с. 802–815
- J. E. Beasley, Bounds for Two-Dimensional Cutting — The Journal of the Operation Research Society, Vol. 36, No. 1 (Jan. 1985) с. 71–74.







