Процессы, протекающие при высыхании капель и тонких пленок жидкостей, содержащих растворенные вещества или взвешенные частицы (истинных и коллоидных растворов), интересны с теоретической и практической сторон. В настоящее время эти процессы используются в литографии, медицине, в области нанотехнологий. При высыхании капли раствора на подложке при обычных условиях испарения частицы вещества выносятся на край капли и образуют кольцо осадка вдоль закрепленной трехфазной границы [1] (так называемый «эффект кофейного кольца»). Условия испарения влияют на процесс перераспределения частиц растворенного в капле или пленке вещества и, следовательно, на образование различных структур из осажденных на подложку частиц [1, 2, 3]. В работах [3, 4, 5] приводятся экспериментальные данные по перераспределению и осаждению на подложку сферических твердых микрочастиц кремния и наночастиц полистирола при испарении водных растворов этих частиц. Пленки растворов помещались на горизонтальные стеклянные подложки и накрывались сверху масками с круглыми отверстиями, образующими гексагональную плоскую решетку. При высыхании в таких условиях частицы вещества перемещались под отверстия в маске и создавали структуру осадка, повторяющую структуру в расположении отверстий.
- Описание модели
Рассматривается тонкая пленка водного раствора, испаряющаяся на горизонтальной твердой подложке при неоднородных условиях испарения. Непосредственно над пленкой располагается плоская непроницаемая маска с круглыми отверстиями, образующими правильную периодическую структуру. Каждое отверстие имеет радиус rh и окружено шестью ближайшими отверстиями, расстояние между центрами отверстий — 𝑃. Радиус отверстий и расстояние между ними малы по сравнению с характерным горизонтальным размером пленки, поэтому структуру отверстий будем считать бесконечно протяженной и не рассматривать эффекты на краях маски. Плоскость маски можно разбить на правильные шестиугольники со стороной ![]() , в центре каждого шестиугольника расположено отверстие (см. рис. 1). Предполагается, что испаряющийся с поверхности раствора пар может выходить в атмосферу только через отверстия.
, в центре каждого шестиугольника расположено отверстие (см. рис. 1). Предполагается, что испаряющийся с поверхности раствора пар может выходить в атмосферу только через отверстия.
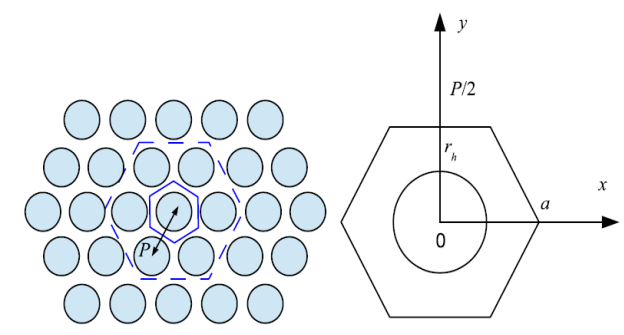
Рис. 1. Фрагмент маски с круглыми отверстиями
Твердая подложка является непроницаемой для раствора. Температура подложки, пленки и атмосферы считается постоянной величиной; таким образом тепловые эффекты в модели не учитываются.
Раствор состоит из растворителя и твердых частиц радиусом r, объемная доля которых в растворе 𝑊. Коэффициент диффузии частиц 𝐷 в модели является постоянным, частицы между собой не взаимодействуют и на скорость течения не влияют. Будем также считать, что взвешенные частицы не влияют на испарение. Для справедливости таких предположений требуется, чтобы объемная доля 𝑊 частиц в растворе была небольшой (𝑊≪1). Пленка раствора будет тонкой и достаточно протяженной, чтобы при отсутствии маски над ней поверхность пленки можно было считать плоской. При испарении под различными препятствиями, как показывает эксперимент [1], поверхность жидкости уже не будет плоской, однако в нашей модели мы не будем это учитывать. Скорость понижения высоты пленки ℎ из-за испарения растворителя будет считаться постоянной величиной, что согласуется с экспериментальными фактами для испарения чистых жидкостей и растворов с небольшой концентрацией растворенных частиц [2]. Таким образом, примем:
![]() (1)
(1)
где ![]() — время полного испарения пленки раствора, начальная высота пленки — ℎ0.
— время полного испарения пленки раствора, начальная высота пленки — ℎ0.
Плотность воды l считаем постоянной величиной. Для тонкой пленки при медленном испарении зависимость параметров раствора от глубины будет слабой, поэтому можно перейти к усредненным по высоте пленки величинам: ![]() — усредненная по высоте раствора скорость течения; 𝑊 — усредненная по высоте раствора объемная доля твердых частиц. В начальный момент времени 𝑊 = 𝑊0. Исходя из симметрии модели, решать задачу распределения частиц вещества в растворе при испарении растворителя достаточно для одной шестиугольной ячейки (см. рис. 1), через боковые грани которой нет потоков жидкости и твердых частиц. При этих предположениях закон сохранения растворителя и растворенных частиц для усредненных 𝑊 и
— усредненная по высоте раствора скорость течения; 𝑊 — усредненная по высоте раствора объемная доля твердых частиц. В начальный момент времени 𝑊 = 𝑊0. Исходя из симметрии модели, решать задачу распределения частиц вещества в растворе при испарении растворителя достаточно для одной шестиугольной ячейки (см. рис. 1), через боковые грани которой нет потоков жидкости и твердых частиц. При этих предположениях закон сохранения растворителя и растворенных частиц для усредненных 𝑊 и ![]() имеет вид:
имеет вид:
![]() (3)
(3)
В уравнениях (2) и (3) дифференциальные операторы ![]() и
и ![]() являются двумерными. Последнее слагаемое в уравнении (3) связано с осаждением частиц на подложку. Если осаждения не учитывать, то это слагаемое обращается в нуль. 𝐽e — плотность потока пара с поверхности раствора, 𝐽s —плотность потока осаждения частиц, 𝜌s —плотность твердых частиц. Уравнение (3) можно назвать уравнением конвекции–диффузии с учетом осаждения.
являются двумерными. Последнее слагаемое в уравнении (3) связано с осаждением частиц на подложку. Если осаждения не учитывать, то это слагаемое обращается в нуль. 𝐽e — плотность потока пара с поверхности раствора, 𝐽s —плотность потока осаждения частиц, 𝜌s —плотность твердых частиц. Уравнение (3) можно назвать уравнением конвекции–диффузии с учетом осаждения.
Уравнения (2), (3) после подстановки (1) можно преобразовать к следующему виду:
![]() (4)
(4)
![]() (5)
(5)
Изменение массы растворителя в шестигранной ячейке определяется испарением с поверхности 𝜎 раствора в ячейке, так как через боковые грани и основание нет потока растворителя. Следовательно,
![]() (6)
(6)
Если объемная доля твердых частиц мала, 𝑊 ≪ 1, то уравнение (6) с учетом (1) можно приближенно записать
![]() (7)
(7)
где 𝑆 — площадь основания шестигранной ячейки ![]() . Из (7) получаем время испарения пленки
. Из (7) получаем время испарения пленки
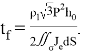 (8)
(8)
Сделаем переход к безразмерным величинам. В качестве характерного времени выбираем ![]() , характерной скорости
, характерной скорости 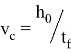 — скорость понижения высоты пленки, характерного геометрического размера —
— скорость понижения высоты пленки, характерного геометрического размера — ![]() .
.
Уравнения (2.4) и (2.5) в безразмерной форме будут иметь вид
![]() (9)
(9)
![]() (10)
(10)
Здесь
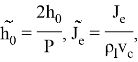
число Пекле —
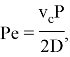
𝐾 — безразмерное число, равное отношению скорости осаждения к характерной скорости. Поток осаждающихся частиц считается пропорциональным концентрации этих частиц аналогично модели [?]. В дальнейшем безразмерные величины будут обозначаться без «тильды».
Для определения плотности потока пара через отверстие в маске предполагалось, что скорость испарения определяется диффузией молекул пара через тонкий слой насыщенного пара над пленкой в окружающую атмосферу. В модели решалось уравнение диффузии пара для квазистационарного случая или уравнение Лапласа для концентрации 𝐶 молекул пара в атмосфере над раствором с маской (над шестигранной ячейкой)
Плотность потока пара
![]() (12)
(12)
где ![]() — коэффициент диффузии пара в атмосфере. При этом считалось, что пар через маску не проходит, непосредственно в отверстии маски пар был насыщенным 𝐶 = 𝐶sat, а вдали от раствора 𝐶 = 𝐻𝐶sat, где 𝐻 — влажность воздуха. Параметры модели были близки к эксперименту, описанному в [2], rh = 125 мкм, 𝑃 = 10𝑟h, 𝑊0 = 510–3 и 𝑊0 = 510–2 ℎ0 = 100 мкм. Параметрами модели были число Пекле и постоянная 𝐾, которые принимали значения Pe = 0,1 и 1, 𝐾 = 0 и 0,5. Модель рассчитывалась численно на компьютере с помощью пакета FlexPDE.
— коэффициент диффузии пара в атмосфере. При этом считалось, что пар через маску не проходит, непосредственно в отверстии маски пар был насыщенным 𝐶 = 𝐶sat, а вдали от раствора 𝐶 = 𝐻𝐶sat, где 𝐻 — влажность воздуха. Параметры модели были близки к эксперименту, описанному в [2], rh = 125 мкм, 𝑃 = 10𝑟h, 𝑊0 = 510–3 и 𝑊0 = 510–2 ℎ0 = 100 мкм. Параметрами модели были число Пекле и постоянная 𝐾, которые принимали значения Pe = 0,1 и 1, 𝐾 = 0 и 0,5. Модель рассчитывалась численно на компьютере с помощью пакета FlexPDE.
- Полученные результаты
На рисунке 2 представлена рассчитанная зависимость плотности потока пара Je от координаты 𝑦 (см. рис. 1) непосредственно над ячейкой с маской. В эксперименте между маской и пленкой была щель, которая увеличивалась, по-видимому, при испарении (эти детали в описании эксперимента отсутствуют). В модели, в отличие от эксперимента, щель между маской и пленкой считалась равной нулю все время испарения, поэтому плотность потока пара не менялась со временем. Плотность потока пара возрастает к краю щели (безразмерный радиус щели равен 0,2) и затем резко уменьшается до нуля.
На рис. 3 представлена полученная скорость течения (усредненная по высоте пленки радиальная составляющая скорости) в зависимости от 𝑦 координаты. Величина скорости максимальна у края отверстия в маске, скорость направлена к центру отверстия, куда течениями переносятся частицы твердого вещества. Следовательно, за счет течений объемная доля частиц в растворе должна быть максимальной под отверстием. Рисунки 4, 5, 6 и 7 иллюстрируют это поведение: объемная доля 𝑊 частиц твердого вещества имеет максимум под отверстием.
С течением времени объемная доля частиц под отверстием в маске увеличивается (см. рис. 4), ширина максимума также увеличивается. Учет осаждения частиц на твердую подложку приводит к уменьшению объемной доли частиц в растворе (см. рис. 5) и к уменьшению высоты максимума под отверстием. Для величины параметра 𝐾 < 4 уменьшение объемной доли частиц в растворе за счет осаждения не перекрывает процесс увеличения 𝑊 за счет испарения. Для 𝐾 > 4 с течением времени объемная доля частиц в растворе начинает уменьшаться.
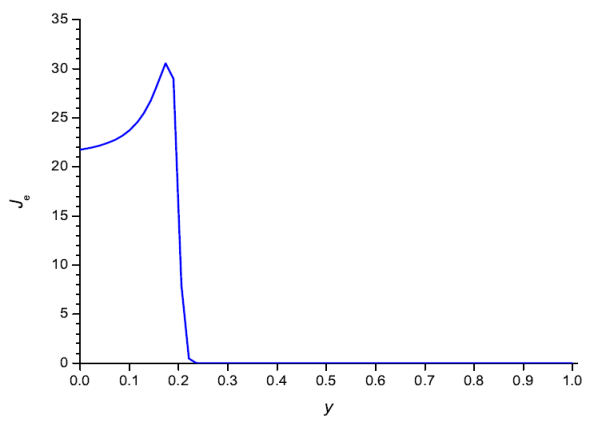
Рис. 2. Плотность потока пара Je непосредственно над ячейкой с маской
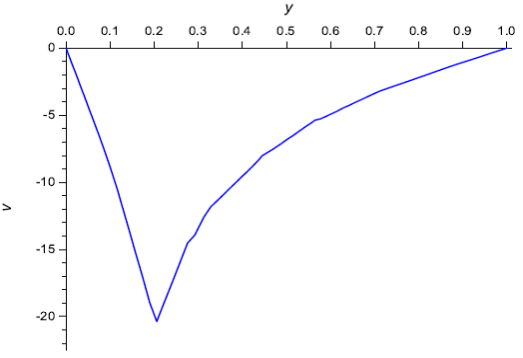
Рис. 3. Зависимость усредненной по высоте пленки радиальной скорости течения ![]() от координаты y в момент времени 0,25
от координаты y в момент времени 0,25![]() , Ре = 1.
, Ре = 1.
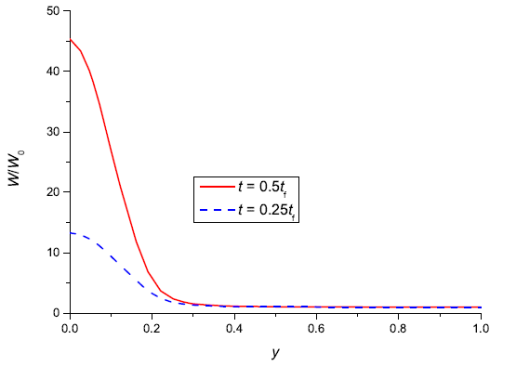
Рис. 4. Зависимость усредненной по высоте объемной доли твердых частиц вещества 𝑊 от координаты у в момент времени 0,25tf (штриховая линия) и 0,5tf (сплошная линия), Ре = 1, К = 0, 𝑊0 =0,005
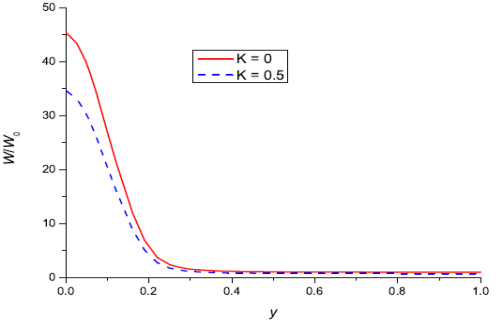
Рис.5. Зависимость усредненной по высоте объемной доли твердых частиц вещества W от координаты y в момент времени 0,5![]() без учета (К = 0, сплошная линия) и с учетом (К = 0,5, штриховая линия) осаждения частиц на подложку, W0 =0,005, Pe =1
без учета (К = 0, сплошная линия) и с учетом (К = 0,5, штриховая линия) осаждения частиц на подложку, W0 =0,005, Pe =1
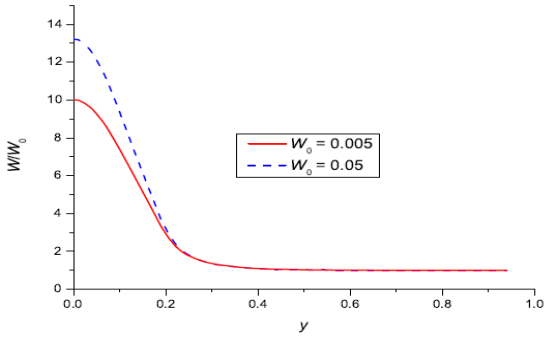
Рис. 6. Зависимость усредненной по высоте объемной доли твердых частиц вещества W от координаты y в момент времени 0,25![]() для двух значений начальной объемной доли W0 =0,005 (сплошная линия) и 0,05 (штриховая линия), Pe =1, K =0
для двух значений начальной объемной доли W0 =0,005 (сплошная линия) и 0,05 (штриховая линия), Pe =1, K =0
Увеличение начальной объемной доли частиц W0 приводит к увеличению числа частиц под отверстием (см. рис. 6). Уменьшение числа Пекле, то есть увеличение роли диффузии частиц приводит к размыванию максимума (см. рис. 7).
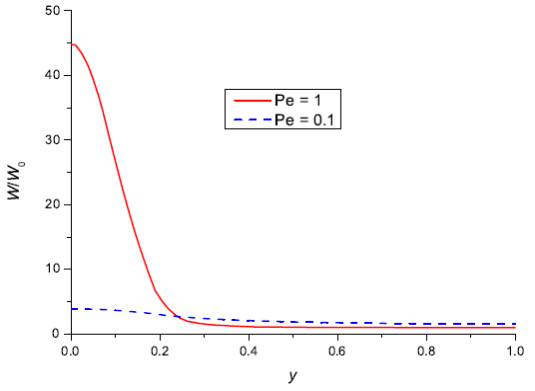
Рис. 7. Зависимость усредненной по высоте объемной доли твердых частиц вещества 𝑊 от координаты 𝑦 в момент времени 0,5![]() для двух значений числа Пекле Pe = 1 (сплошная линия) и 0,1 (штриховая линия), 𝐾=0, 𝑊0 = 0,005.
для двух значений числа Пекле Pe = 1 (сплошная линия) и 0,1 (штриховая линия), 𝐾=0, 𝑊0 = 0,005.
Литература:
- Contact line deposits in an evaporating drop / R. D. Deegan, O. Bakajin, T. F. Dupont [et al.] // Physical Review E. — 2000. — Jul. — Vol. 62, no. 1. — P. 756–765. http://dx.doi.org/10.1103/PhysRevE.62.756
- Dips and rims in dried colloidal films / C. Parneix, P. Vandoolaeghe, V. S. Nikolayev [et al.] // Phys. Rev. Lett. — 2010. — Dec. — Vol. 105. — P. 266103. http://dx.doi.org/10.1103/PhysRevLett.105.266103
- Patterning colloidal films via evaporative lithography / D. J. Harris, H. Hu, J. C. Conrad, J. A. Lewis // Physical Review Letters. — 2007. — Apr. — Vol. 98, no. 14. — P. 148301. http://dx.doi.org/10.1103/PhysRevLett.98.148301
- Harris, D. J. Marangoni effects on evaporative lithographic patterning of colloidal films / D. J. Harris, J. A. Lewis // Langmuir. — 2008. — Vol. 24, no. 8. — P. 3681–3685. http://dx.doi.org/10.1021/la8000637
- Harris, D. J. Evaporative lithographic patterning of binary colloidal films / D. J. Harris, J. C. Conrad, J. A. Lewis // Philosophical Transactions of the Royal Society A: Mathematical,Physical and Engineering Sciences. — 2009. — Vol. 367, no. 1909. — P. 5157–5165. http://dx.doi.org/10.1098/rsta.2009.0157
- Film formation kinetics in the drying process of polymer solution enclosed by bank / Y. Jung, T. Kajiya, T. Yamaue, M.. Doi // Japanese Journal of Applied Physics. — 2009. — Vol. 48. — P. 031502. http://dx.doi.org/10.1143/JJAP.48.031502
- Widjaja, E. Particle deposition study during sessile drop evaporation / E. Widjaja, M. Harris // AIChE J. — 2008. — September. — Vol. 54, no. 9. — P. 2250–2260. http://dx.doi.org/10.1002/aic.11558







